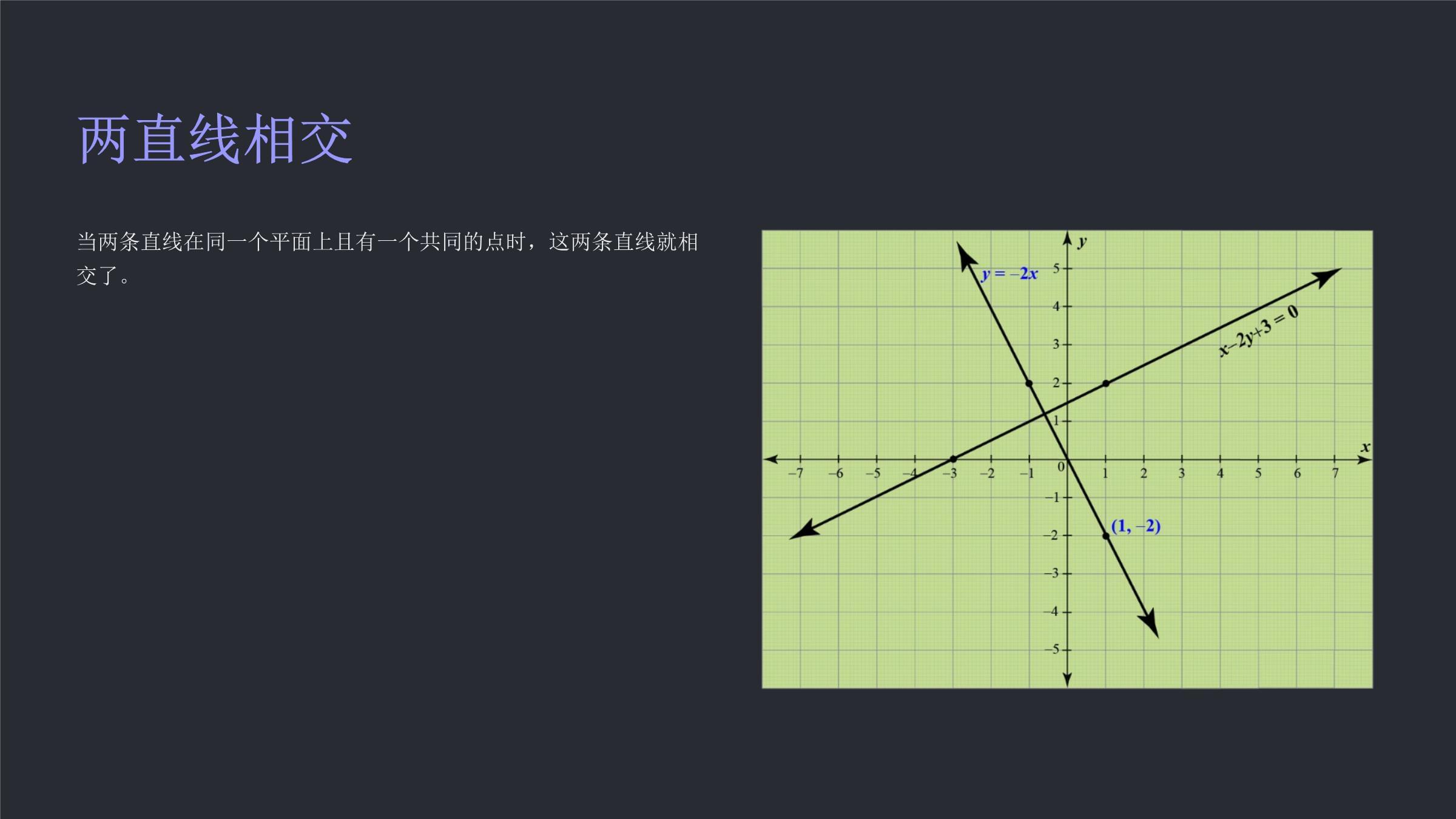
兩直線的位置關系-夾角本課件將深入探討兩直線的位置關系，包括平行、相交、垂直，并介紹兩直線之間的夾角概念。學習目標了解兩直線的位置關系掌握兩直線夾角的概念和計算方法能夠運用兩直線的位置關系和夾角解決實際問題兩直線相交當兩條直線在同一個平面上且有一個共同的點時，這兩條直線就相交了。相交點兩條直線相交，它們有一個公共點。這個公共點叫做**相交點**。相交角相交角的定義兩條直線相交形成的四個角，稱為相交角。相交角的性質相交角的兩組對頂角相等，同旁內角互補。相交角的定義定義兩條直線相交形成的四個角，叫做相交角。圖形如上圖所示，直線l和m相交于點O，形成四個相交角：∠1，∠2，∠3，∠4。相交角的性質對頂角相等兩條直線相交形成的四個角中，兩個相對的角叫做對頂角。對頂角相等。鄰補角互補兩條直線相交形成的四個角中，相鄰的兩個角叫做鄰補角，它們互補，即它們的度數之和等于180°。相交直線的特殊情況當兩條直線相交時，它們可能形成一些特殊的角度關系。例如，當兩條直線互相垂直時，它們形成的四個角都是直角，每個角都是90度。如果兩條直線互相平行，它們形成的四個角都是相等的，并且每個角都是180度的一半，也就是90度。兩直線平行定義在同一平面內，不相交的兩條直線叫做平行線。符號用“//”表示兩條直線平行，例如：直線a//直線b。例子鐵軌、街道等都是平行線的例子。平行線的定義定義在同一平面內，不相交的兩條直線叫做平行線。符號用“//”表示平行，例如：直線AB//直線CD。平行線的判定內錯角相等當兩條直線被第三條直線所截，如果內錯角相等，則這兩條直線平行。同位角相等當兩條直線被第三條直線所截，如果同位角相等，則這兩條直線平行。同旁內角互補當兩條直線被第三條直線所截，如果同旁內角互補，則這兩條直線平行。平行線的性質等距平行線之間的距離處處相等。同位角相等兩條平行線被第三條直線所截，同位角相等。內錯角相等兩條平行線被第三條直線所截，內錯角相等。同旁內角互補兩條平行線被第三條直線所截，同旁內角互補。平行線的應用1建筑設計建筑物中的平行線，如窗戶或門框，可以創造出視覺上的平衡和穩定感。2繪畫與藝術藝術家使用平行線來創造深度、透視和運動感。3工程與制造平行線在工程設計中至關重要，例如鐵路軌道或橋梁。兩直線垂直兩條直線相交，且夾角為90度，則稱這兩條直線垂直。垂直關系是幾何圖形中常見的概念，也是重要的數學工具。垂直的定義垂直線兩條直線相交成直角，我們就說這兩條直線互相垂直。垂直符號用符號“⊥”表示垂直，例如：直線AB垂直于直線CD，記作AB⊥CD。垂直的判定定義兩條直線相交成直角，則稱這兩條直線互相垂直。判定方法若兩條直線的斜率乘積為-1，則這兩條直線互相垂直。特殊情況當兩條直線中有一條是水平線或垂直線時，可以通過觀察判斷兩條直線是否互相垂直。垂直線的特殊情況當兩條直線互相垂直時，它們形成的夾角為90度，也稱為直角。在平面幾何中，垂直線具有許多特殊的性質，例如：兩條垂直線的斜率乘積為-1。垂直線的特殊情況包括：兩條平行線的公垂線、直線與圓的切線等等。直線的傾斜角直線的傾斜角指的是直線與x軸正方向所成的角.傾斜角的范圍是0°到180°，不包括180°.傾斜角的定義水平線水平線是與水平面平行的直線。傾斜角傾斜角是指一條直線與水平線的夾角，它描述了這條直線相對于水平面的傾斜程度。傾斜角的計算公式傾斜角的正切等于斜率，即tanθ=k步驟1.利用直線方程求出斜率k2.利用反三角函數計算傾斜角θ=arctank舉例若直線方程為y=2x+1，則斜率k=2，傾斜角θ=arctan2≈63.4°斜率的計算1公式直線的斜率等于直線上任意兩點縱坐標之差與橫坐標之差的比值，即：k=(y2-y1)/(x2-x1)2實例例如，直線上兩點A(1,2)和B(3,4)，則直線的斜率k=(4-2)/(3-1)=1。3注意事項當直線垂直于x軸時，斜率不存在；當直線與x軸平行時，斜率為0。斜率的性質斜率不變性一條直線上任意兩點的斜率都相等。斜率與直線傾斜角的關系直線的斜率等于其傾斜角的正切值。斜率與直線位置的關系斜率為正的直線向上傾斜，斜率為負的直線向下傾斜。垂直線的斜率1斜率不存在垂直線的斜率不存在，因為垂直線上的所有點都具有相同的橫坐標。2公式垂直線的斜率可以用公式表示為：m=∞(無窮大)。3概念這表示垂直線的斜率是一個無限大的值，這意味著垂直線沒有明顯的傾斜方向。平行線的斜率相同斜率平行直線的斜率相等，表示它們在坐標系中具有相同的傾斜程度。不同斜率如果兩條直線的斜率不同，則它們不平行，它們會在坐標系中相交。夾角的大小1銳角小于90度的角。2直角等于90度的角。3鈍角大于90度且小于180度的角。銳角、鈍角和直角銳角小于90度的角。鈍角大于90度但小于180度的角。直角等于90度的角。角度的單位轉換度最常見的角度單位，用符號°表示。弧度以圓心角所對的弧長與半徑之比表示的角度單位，用符號rad表示。兩直線夾角的計算1公式tanθ=|(