2023屆安徽省蒙城中學初三3月適應性考試（零模）數學試題

考生請注意：

1.答題前請將考場、試室號、座位號、考生號、姓名寫在試卷密封線內，不得在試卷上作任何標記。

2.第一部分選擇題每小題選出答案后，需將答案寫在試卷指定的括號內，第二部分非選擇題答案寫在試卷題目指定的

位置上。

3.考生必須保證答題卡的整潔。考試結束后，請將本試卷和答題卡一并交回。

一、選擇題（本大題共12個小題，每小題4分，共48分,在每小題給出的四個選項中，只有一項是符合題目要求的.）

1.在一些美術字中，有的漢字是軸對稱圖形.下面4個漢字中，可以看作是軸對稱圖形的是（）

A.中B.國C.艾^D,彳名

2.已知線段AB=8cm,點C是直線AB上一點，BC=2cm,若M是AB的中點，N是BC的中點，則線段MN的長

度為（）

A.5cmR.5cm或3rmC.7cm或3cmD.7cm

3.如圖所示的幾何體的主視圖是（）

正?

A.|||

4.如圖，立體圖形的俯視圖是（）

B-F^rD.

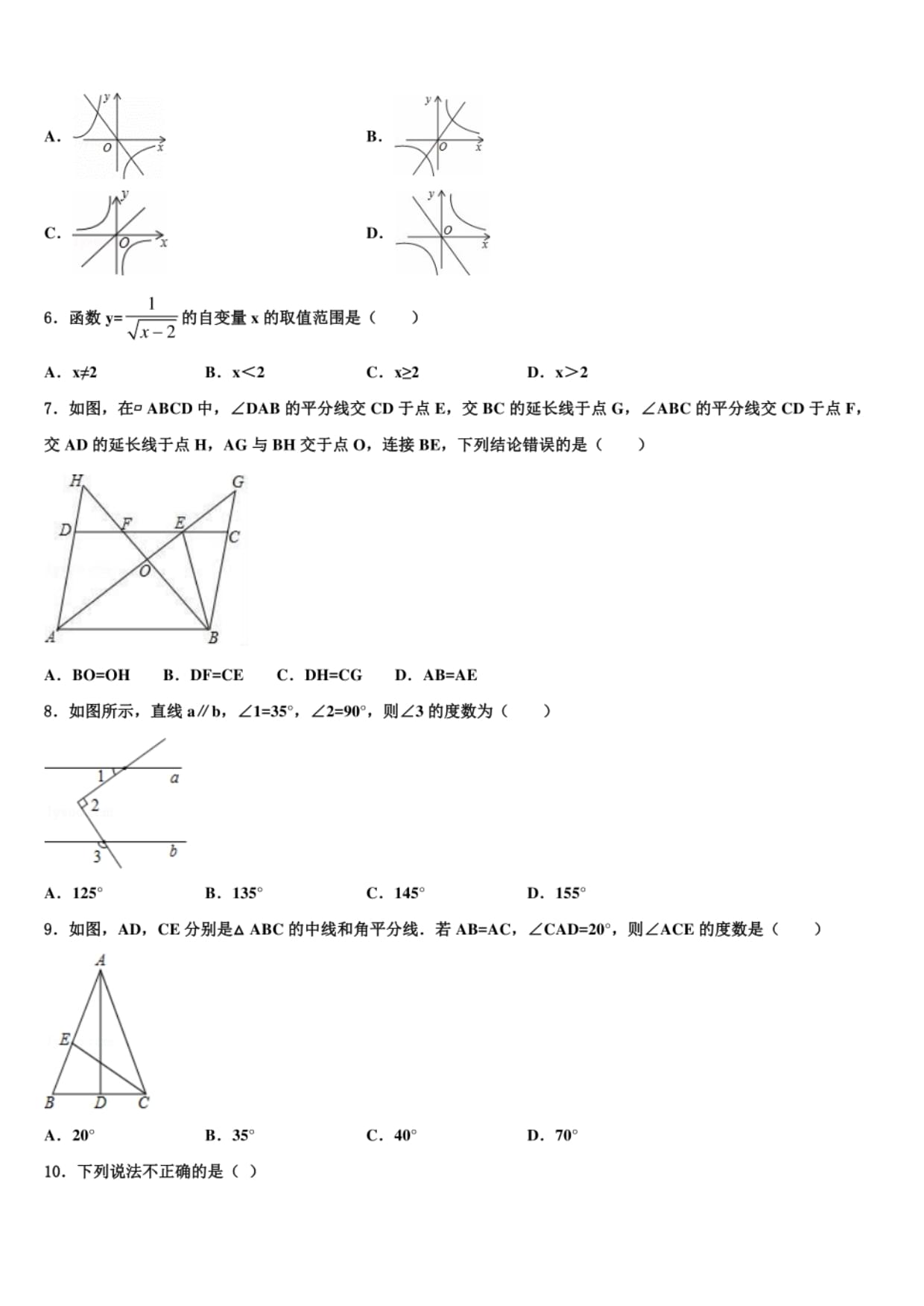
5.已知一次函數尸kx+b的圖象如圖，那么正比例函數丫=卜和反比例函數y=2在同一坐標系中的圖象的形狀大致是

X

(

7.如圖，在口ABCD中，NDAB的平分線交CD于點E,交BC的延長線于點G,NABC的平分線交CD于點F,

交AD的延長線于點H,AG與BH交于點O,連接BE,下列結論錯誤的是（）

9.如圖，AD,CE分別是△ABC的中線和角平分線.若AB=AC,ZCAD=20°,則NACE的度數是（)

C.40D.70°

10.下列說法不正確的是（）

A.某種彩票中獎的概率是7;上，買1000張該種彩票一定會中獎

1000

B.了解一批電視機的使用壽命適合用抽樣調查

C.若甲組數據的標準差S*0.31,乙組數據的標準差S片0.25,則乙組數據比甲組數據穩定

D.在一個裝有白球和綠球的袋中摸球，摸出黑球是不可能事件

11.隨機擲一枚均勻的硬幣兩次，至少有一次正面朝上的概率為（）

12.如果零上2c記作+2C,那么零下34c記作（）

A.-3*CB.-2cC.+3CD.+2C

二、填空題：（本大題共6個小題，每小題4分，共24分.）

13.如圖，已知函數y=x+2的圖象與函數（A和）的圖象交于4、B兩點,連接80并延長交函數y=&（到0）

XX

的圖象于點C,連接AC,若AABC的面積為1.則人的值為.

14.科技改變生活，手機導航極大方便了人們的出行.如圖，小明一家自駕到古鎮C游玩，到達4地后，導航顯示車

輛應沿北偏西60。方向行駛6千米至3地，再沿北偏東45。方向行駛一段距離到達古鎮C.小明發現古鎮。恰好在A

地的正北方向，則3、C兩地的距離是千米.

15.一個不透明的袋子中裝有5個球，其中3個紅球、2個黑球，這些球除顏色外無其它差別，現從袋子中隨機摸出

一個球，則它是黑球的概率是.

16.如圖，在平面直角坐標系中，矩形活動框架ABCD的長AB為2,寬AD為段,其中邊AB在x軸上，且原點

6為AB的中點，固定點A、B,把這個矩形活動框架沿箭頭方向推，使D落在y軸的正半軸上點D，處，點C的對應

點C'的坐標為.

17.如圖，半徑為3的。O與RtAAOB的斜邊AB切于點D,交OB于點C,連接CD交直線OA于點E,若NB=30。,

則線段AE的長為.

18.一個長方體的三視圖如圖所示，若其俯視圖為正方形，則這個長方體的體積為

①他山

主視圖左視圖

O

俯視圖

三、解答題：（本大題共9個小題，共78分，解答應寫出文字說明、證明過程或演算步驟.

19.（6分）如圖，已知A（-4,!）,B（-Jl,m）是一次函數y=kx+b與反比例函數y二2圖象的兩個交點，AC±x

2x

軸于點C,BD_Ly軸于點D.

（1）求m的值及一次函數解析式;

（2）P是線段AB上的一點，連接PC、PD,若APCA和APDB面積相等，求點P坐標.

2x>x_1@

20.（6分）解不等式組

L3(L2?4②

請結合題意填空，完成本題的解答

（1）解不等式①，得.

（2）解不等式②，得.

（3）把不等式①和②的解集在數軸上表示出來：

-3-2-1~0~1~2-3^

（4）原不等式組的解集為.

21.（6分）每到春夏交替時節，雌性楊樹會以滿天飛絮的方式來傳播下一代，漫天飛舞的楊絮易引發皮膚病、呼吸道

疾病等，給人們造成困擾，為了解市民對治理楊絮方法的贊同情況，某課題小組隨機調查了部分市民（問卷調查表如

表所示），并根據調查結果繪制了如下尚不完整的統計圖.

治理楊絮一一您選哪一項？（單選）

A.減少楊樹新增面積，控制楊樹每年的栽種量

B.調整樹種結構，逐漸更換現有楊樹

C.選育無素楊品種，并推廣種植

D.對雌性楊樹注射生物干擾素，避免產生飛絮

調查結果條形統計圖

800

5

4oo

3oo

2oo

1oo

oo

ABCDE嘉項

根據以上統計圖，解答下列問題：

（1）本次接受調查的市民共有人；

（2）扇形統計圖中，扇形E的圓心角度數是；

（3）請補全條形統計圖；

（4）若該市約有90萬人，請估計贊同“選育無絮楊品種，并推廣種植”的人數.

22.（8分）作圖題：在NABC內找一點P,使它到NA3C的兩邊的距離相等，并且到點A、。的距離也相等.（寫出

作法，保留作圖痕跡）

I+6tan30°

24.(10分)在正方形ABCD中，動點E,尸分別從0,。兩點同時出發，以相同的速度在直線DC,上移動.

(1)如圖1,當點￡在邊OC上自。向C移動，同時點尸在邊C3上自C向6移動時，連接AE和。尸交于點P,請

你寫出AE與OF的數量關系和位置關系，并說明理由;

(2)如圖2,當E,尸分別在邊CD,8c的延長線上移動時，連接DF,(1)中的結論還成立嗎？(請你直接回

答“是”或“否”，不需證明)；連接4C,請你直接寫出A4C比為等腰三角形時CE：CO的值;

(3)如圖3,當E,尸分別在直線DC,上移動時，連接AE和。尸交于點尸，由于點E,尸的移動，使得點尸也

隨之運動，請你畫出點尸運動路徑的草圖.若AO=2,試求出線段CP的最大值.

25.(10分)水龍頭關閉不緊會造成滴水，小明用可以顯示水量的容器做圖①所示的試驗，并根據試驗數據繪制出圖

②所示的容器內盛水量W(L)與滴水時間t(h)的函數關系圖象，請結合圖象解答下列問題：容器內原有水多少?

求W與t之間的函數關系式，并計算在這種滴水狀態下一天的滴水量是多少升?

26.(12分)如圖，在△ABC中，ZABC=90°?D,E分別為AB,AC的中點，延長DE到點F,使EF=2DE.

(1)求證：四邊形BCFE是平行四邊形；

(2)當NACB=60。時，求證：四邊形BCFE是菱形.

BC

27.(12分)如圖所示，△ABC和△ADE是有公共頂點的等腰直角三角形，ZBAC=ZDAE=90°,EC的延長線交BD

于點P.

(1)把△ABC繞點A旋轉到圖1,BD,CE的關系是(選填“相等”或“不相等”)；簡要說明理由；

(2)若AB=3,AD=5,把△ABC繞點A旋轉，當NEAC=90"。時，在圖2中作出旋轉后的圖形，PD=,簡要

說明計算過程；

(3)在(2)的條件下寫出旋轉過程中線段PD的最小值為,最大值為.

參考答案

一、選擇題(本大題共12個小題，每小題4分，共48分.在每小題給出的四個選項中，只有一項是符合題目要求的

1、A

【解析】

根據軸對稱圖形的概念判斷即可.

【詳解】

A、是軸對稱圖形；

B、不是軸對稱圖形；

C、不是軸對稱圖形；

D、不是軸對稱圖形.

故選：A.

【點睛】

本題考查的是軸對稱圖形的概念.軸對稱圖形的關鍵是尋找對稱軸，圖形兩部分擰疊后可重合.

2、B

【解析】

(1)如圖1,當點C在點A和點B之間時，

???點M是AB的中點，點N是BC的中點，AB=8cm,BC=2cm,

11

??MB=—AB=4cm,BN=—BC=lcm,

22

/.MN=MB-BN=3cm；

(2)如圖2,當點C在點B的右側時，

???點M是AB的中點，點N是BC的中點，AB=8cm,BC=2cm,

11

MB=—AB=4cm,BN=—BC=lcm,

22

,MN=MB+BN=5cm.

綜上所述，線段MN的長度為5cm或3cm.

故選B.

AMCNBAMBNC

rai圖2

點睛：解本題時，由于題目中告訴的是點C在直線AB上，因此根據題目中所告訴的AB和BC的大小關系要分點C

在線段AB上和點C在線段AB的延長線上兩種情況分析解答，不要忽略了其中任何一種.

3、A

【解析】

找到從正面看所得到的圖形即可.

【詳解】

解：從正面可看到從左往右2列一個長方形和一個小正方形，

故選A.

【點睛】

本題考查了三視圖的知識，主視圖是從物體的正面看得到的視圖.

4、C

【解析】

試題分析：立體圖形的俯視圖是C.故選C.

考點：簡單組合體的三視圖.

5、C

【解析】

試題分析：如圖所示，由一次函數y=kx+b的圖象經過第一、三、四象限，可得k>l,b<l,因此可知正比例函數尸kx

的圖象經過第一、三象限，反比例函數y=2的圖象經過第二、四象限.綜上所述，符合條件的圖象是C選項.

x

故選C.

考點：1、反比例函數的圖象；2、一次函數的圖象；3、一次函數圖象與系數的關系

6、D

【解析】

根據被開放式的非負性和分母不等于零列出不等式即可解題.

【詳解】

1

解：■:函數y=I——有意義,

Vx-2

Ax-2>0,

即x>2

故選I)

【點睛】

本題考查了根式有意義的條件，屬于簡單題，注意分母也不能等于零是解題關鍵.

7、D

【解析】

解：???四邊形ABCD是平行四邊形，：.AH//BGfAD=BCtVZHBG=ZHBAt；./H=NHBA,

同理可證8G=48,：,AH=BG.*：AD=BCt：.DH=CG,故C正確.

?：AH=AB,NOAH=NOAB,：?OH=OB,故A正確.

?:DF〃AB,：?/DFH=/ABH.?:/H=NABH,:?NH=/DFH,,DF=DH.

同理可證EC=CG.

\'DH=CGr:,DF=CE,故B正確.

無法證明AE=A小故選D.

8、A

【解析】

分析：如圖求出N5即可解決問題.

詳解：

Va/7b,

，N1=N4=35°,

?:Z2=90°,

/.Z4+Z5=90o,

AZ5=55°,

AZ3=180°-Z5=125°,

故選：A.

點睛：本題考查平行線的性質、三角形內角和定理，鄰補角的性質等知識，解題的關鍵是靈活運用所學知識解決問題.

9、B

【解析】

先根據等腰三角形的性質以及三角形內角和定理求出NCAB=2NCAD=40。，ZB=ZACB=-(180°-ZCAB)=70°.再

2

利用角平分線定義即可得出NACE=LZACB=35°.

2

【詳解】

YAD是△ABC的中線，AB=AC,ZCAD=20°,

AZCAB=2ZCAD=40°,ZB=ZACB=-(1800-ZCAB)=70°.

2

???CE是△ABC的角平分線，

AZACE=-ZACB=35°.

2

故選B.

【點睛】

本題考查了等腰三角形的兩個底角相等的性質，等腰三角形的頂角平分線、底邊上的中線、底邊上的高相互重合的性

質，三角形內角和定理以及角平分線定義，求出NACB=70。是解題的關鍵.

10、A

【解析】

試題分析：根據抽樣調查適用的條件、方差的定義及意義和可能性的大小找到正確答案即可.

試題解析：A、某種彩票中獎的概率是焉，只是一種可能性，買1000張該種彩票不一定會中獎，故錯誤；

B、調查電視機的使用壽命要毀壞電視機，有破壞性，適合用抽樣調查，故正確；

C、標準差反映了一組數據的波動情況，標準差越小，數據越穩定，故正確；

D、袋中沒有黑球，摸出黑球是不可能事件，故正確.

故選A.

考點：1.概率公式；2.全面調查與抽樣調查；3.標準差；4.隨機事件.

11、D

【解析】

先求出兩次擲一枚硬幣落地后朝上的面的所有情況，再根據概率公式求解.

【詳解】

隨機擲一枚均勻的硬幣兩次，落地后情況如下：

正反

AA

IF反正反

3

至少有一次正面朝上的概率是

4

故選：D.

【點睛】

本題考查了隨機事件的概率，如果一個事件有〃種可能，而且這些事件的可能性相同，其中事件A出現m種結果，那

么事件4的概率P(A)=3.

n

12、A

【解析】

一對具有相反意義的量中，先規定其中一個為正，則另一個就用負表示.

【詳解】

???“正”和“負”相對，，如果零上2c記作+2C,那么零下3c記作一3c.

故選A.

二、填空題：(本大題共6個小題，每小題4分，共24分.)

13、3

【解析】

連接OA.根據反比例函數的對稱性可得OB=OC,那么SAOAB=SAOAC=；SAABC=2.求出直線y=x+2與y軸交點D的

坐標.設A(a,a+2),B(b,b+2),則C(-b,-b-2),根據SAOAB=2,得出a?b=2①.根據SAOAC=2,得出?a?b=2②,

①與②聯立，求出a、b的值，即可求解.

【詳解】

如圖，連接OA.

由題意，可得OB=OC,

：?SAOAB=SAOAC=-SAABC=2.

2

設直線y=x+2與y軸交于點D,則D(0,2),

設A(a,a+2),B(b,b+2),則C(-b,-b-2),

ASAO^\B=—X2X(a-b)=2,

2

Aa-b=2①.

過A點作AMJ_x軸于點M,過C點作CN_Lx軸于點N,

貝I)SAOAM=SAOCN=—k,

2

?'?SAOAC=SAOAM+S梯形AMNC-SAOCN=S梯形AMNC=2,

/.—(-b-2+a+2)(-b-a)=2,

2

將①代入，得

/.-a-b=2②,

①+得?2b=6,b=-3,

①?,得2a=2,a=l,

AA(1,3),

Ak=lx3=3.

故答案為3.

【點睛】

本題考查了反比例函數與一次函數的交點問題，反比例函數的性質，反比例函數圖象上點的坐標特征，三角形的面積,

待定系數法求函數的解析式等知識，綜合性較強，難度適中.根據反比例函數的對稱性得出OB=OC是解題的突破口.

14、3口

【解析】

作BE_LAC于E,根據正弦的定義求出BE,再根據正弦的定義計算即可.

【詳解】

解：作于凡

在RSA3E中，sinZBAC=—，

AB

：?BE=AB*sinZBAC=6x—=3百，

2

由題意得，NC=45。，

：.BC==373=3>/6（千米），

smC2

故答案為3?.

【點睛】

本題考查的是解直角三角形的應用?方向角問題，掌握方向角的概念、熟記銳角三角函數的定義是解題的關鍵.

2

15、-

5

【解析】

用黑球的個數除以總球的個數即可得出黑球的概率.

【詳解】

解：???袋子中共有5個球，有2個黑球，

2

???從袋子中隨機摸出一個球，它是黑球的概率為不；

故答案為|.

【點睛】

本題考查概率的求法：如果一個事件有n種可能，而且這些事件的可能性相同，其中事件A出現m種結果，那么事

件A的概率P(A)=-.

n

16、(2,1)

【解析】

由已知條件得到AD，=AD=JJ,AO=yAB=1,根據勾股定理得到OD，=勺,于是得到結論.

【詳解】

解：VADf=AD=72?AO=yAB=l,

W,心_32=i,

???C'D'=2,C'D'〃AB,

???C'(2,1),

故答案為：(2,1)

【點睛】

本題考查了矩形的性質，坐標與圖形的性質，勾股定理，正確的識別圖形是解題的關鍵.

17、Q

【解析】

要求AE的長，只要求出OA和OE的長即可，要求OA的長可以根據NB=30。和0B的長求得，OE可以根據NOCE

和OC的長求得.

【詳解】

解：連接OD,如圖所示，

由已知可得，ZBOA=90°,OD=OC=3,ZB=30°,ZODB=90°,

???BO=2OD=6,NBOD=60。，

/.ZODC=ZOCD=60°,AO=BOtan300=6x夕技

VZCOE=90°,OC=3,

:.OE=OCtan600=3x相=3技

AAE=OE-4A=3拒-2拒=后

切線的性質

18、1.

【解析】

試題解析：設俯視圖的正方形的邊長為

??,其俯視圖為正方形，從主視圖可以看出，正方形的對角線長為2"

???/+/=(2@:

解得/=4

???這個長方體的體積為4x3=1.

三、解答題：(本大題共9個小題，共78分，解答應寫出文字說明、證明過程或演算步驟.

19、(1)m=2；y=—x+—；(2)P點坐標是(-2，—).

2224

【解析】

(1)利用待定系數法求一次函數和反比例函數的解析式：

(15、

(2)設點P的坐標為Px,-x+-，根據面積公式和已知條件列式可求得上的值，并根據條件取舍，得出點P的坐

I22)

標.

【詳解】

解：(1)??,反比例函數＞的圖象過點(一4，；)，

n=-4x，=—2,

2

???點B(-1,m)也在該反比例函數的圖象上，

:.-l*m=-2,

/.m=2；

設一次函數的解析式為y=kx+b,

由丫=1?+?)的圖象過點從［-4,5),,B(-1,2),則

-4k+b=-

2解得：，

-k+b=2,h=r

???一次函數的解析式為y二;工+1；

(2)連接PC、PD,如圖，設+

VAPCA和乙PDB面積相等,

11(x+4)=1x|-l|x(2-115

—X—Xx——

2222

小組5155

解得：x=——=—x+—=—,

2224

本題考查待定系數法求反比例函數以及一次函數解析式，反比例函數與一次函數的交點問題，熟練掌握待定系數法是

解題的關鍵.

20、(1)x>-l；(2)x<l；(3)見解析；(4)-1<X<1.

【解析】

分別解兩個不等式，然后根據公共部分確定不等式組的解集，再利用數軸表示解集.

【詳解】

解：(1)x>-l；

（2）x<l；

(3)-J-------------X_?_X_?_;

-3-2-1012r

(4)原不等式組的解集為一區爛1.

【點睛】

本題考查了解一元一次不等式組：一般先求出其中各不等式的解集，再求出這些解集的公共部分，利用數軸可以直觀

地表示不等式組的解集.解集的規律：同大取大；同小取小；大小小大中間找；大大小小找不到.

21、(1)2000；(2)28.8°；(3)補圖見解析；(4)36萬人.

【解析】

分析：(D將A選項人數除以總人數即可得；

(2)用360。乘以E選項人數所占比例可得；

(3)用總人數乘以D選項人數所占百分比求得其人數，據此補全圖形即可得：

(4)用總人數乘以樣本中C選項人數所占百分比可得.

詳解：(D本次接受調查的市民人數為300?15%=2000人，

(2)扇形統計圖中，扇形E的圓心角度數是360味黑^=28.8。，

(3)D選項的人數為2000x25%=500,

500

400

300

20()

10。0

(4)估計贊同“選育無絮楊品種，并推廣種植”的人數為90X40%=36(萬人).

點睛：本題考查的是條形統計圖和扇形統計圖的綜合運用.讀懂統計圖，從不同的統計圖中得到必要的信息是解決問

題的關鍵.條形統計圖能清楚地表示出每個項目的數據；扇形統計圖直接反映部分占總體的百分比大小.

22、見解析

【解析】

先作出N4BC的角平分線，再連接AC,作出AC的垂直平分線，兩條平分線的交點即為所求點.

【詳解】

①以耳為圓心，以任意長為半徑畫弧，分別交〃。、于。、E兩點；

②分別以。、￡為圓心，以大于1&￡為半徑畫圓，兩圓相交于尸點;

2

③連接AP,則直線4戶即為NA5C的角平分線；

⑤連接AC,分別以4、C為圓心，以大于!AC為半徑畫圓，兩圓相交于尸、”兩點;

2

本題考查的是角平分線及線段垂直平分線的作法，熟練掌握是解題的關鍵.

23、10+6

【解析】

根據實數的性質進行化簡即可計算.

【詳解】

原式=9?l+2-G+6x立

3

=10-V3+2x/3

=10+6

【點睛】

此題主要考查實數的計算，解題的關鍵是熟知實數的性質.

24、(1)AE=DF,AE±DF,理由見解析；(2)成立，CE:CD=0或2；(3)75+1

【解析】

試題分析：(1)根據正方形的性質，由SAS先證得△ADEg^DCF.由全等三角形的性質得AE=DF,ZDAE=ZCDF,

再由等角的余角相等可得AEXDF；

(2)有兩種情況：①當AC=CE時，設正方形ABCD的邊長為a,由勾股定理求出AC=CE=忘a即可；②當AE=AC

時，設正方形的邊長為a,由勾股定理求出AC=AE;應a,根據正方形的性質知NADC=90。，然后根據等腰三角形的

性質得出DE=CD=a即可；

(3)由(D(2)知：點P的路徑是一段以AD為直徑的圓，設AD的中點為0,連接OC交弧于點P,此時CP的

長度最大，再由勾股定理可得QC的長，再求CP即可.

試題解析：(1)AE=DF,AE±DF,

理由是：???四邊形ABCD是正方形，

/.AD=DC,ZADE=ZDCF=90°,

??,動點E,F分別從D,C兩點同時出發，以相同的速度在直線DC,CB上移動,

.*.DE=CF,

在4ADE和^DCF中

AD=DC

<4ADE=4DCF,

DE=CF

：.MDE=/iDCFt

.\AE=DF,ZDAE=ZFDC,

VZADE=90°,.?.ZADP+ZCDF=90°,

AZADP+ZDAE=90°,

.?.ZAPD=180o-90°=90°,

.\AE±DF；

(2)(1)中的結論還成立，

有兩種情況：

圖1

①如圖1,當AC=CE時，

設正方形ABCD的邊長為a,由勾股定理得,

AC=CE=Ja2+a2=\/2a,

則CE:CD=&。:"夜;

②如圖2,當AE=AC時，

設正方形ABCD的邊長為a,由勾股定理得:

AC=AE=yja2+a2=\[2a，

???四邊形ABCD是正方形，

AZADC=90o,即AD_LCE,

ADE=CD=a,

ACE:CD=2a:a=2：

圖3

即CE:CD=V25E2；

(3)???點P在運動中保持NAPD=90。，

，點P的路徑是以AD為直徑的圓，

如圖3,設AD的中點為Q,連接CQ并延長交圓弧于點P,

此時CP的長度最大，

;在RMQDC中，QC=JCD2+QD2=6+12=也

：.CP=QC+QP=45+\9

即線段CP的最大值是石+1.

點睛：此題主要考查了正方形的性質，勾股定理，圓周角定理，全等三角形的性質與判定，等腰三角形的性質，三角

形的內角和定理，能綜合運用性質進行推擠是解此題的關鍵，用了分類討論思想，難度偏大.

25、(1)0.3L；(2)在這種滴水狀態下一天的滴水量為9.6L.

【解析】

(1)根據點(0,0.3)的實際意義可得；

(2)設W與/之間的函數關系式為W=k+b,待定系數法求解可得，計算出，=24時W的值，再減去容器內原有

的水量即可.

【詳解】

(1)由圖象可知，容器內原有水0?3L.

(2)由圖象可知W與t之間的函數圖象經過點(0,0.3),

故設函數關系式為W=kt+0.3.

又因為函數圖象經過點(1.5,0.9),

代入函數關系式，得1.5k+0.3=0.9,解得k=0.4.

故W與t之間的函數關系式為W=0.4t+0.3.

當t=24時，W=0.4x24+0?3=9.9(L),9.9-03=9.6(L),

即在這種滴水狀態下一天的滴水量為9.6L.

【點睛】

本題考查了一次函數的應用，關鍵是利用待定系數法正確求出一次函數的解析式.

26、(1)見解析；(2)見解析

【解析】

(1)由題意易得，E尸與5c平行且相等，利用四邊形BC尸E是平行四邊形.

(2)根據菱形的判定證明即可.

【詳解】

(1)證明：：VD.E為AB,AC中點

ADE為RABC的中位線，DE=,BC,

ADE/7BC,

即EF/7BC

VEF=BC,

???四邊形BCEF為平行四邊形.

(2)???四邊形BCEF為平行四邊形，

VZACB=60°,

ABC=CE=BE,

???四邊形BCFE是菱形.

A

【點睛】

本題考查平行四邊形的判定和性質、菱形的判定、等邊三角形的判定和性質等知識，解題的關鍵是靈活運用所學知識

解決問題，屬于中考常考題型.

27、(1)BD,CE的關系是相等；(2)亍或yy;(3)1,1

【解析】

分析：(1)依據△ABC和^ADE是有公共頂點的等腰直角三角形，ZBAC=ZDAE=90°,即可BA=CA,ZBAD=ZCAE,

DA=EA,進而得到4ABD^AACE,可得出BD=CE；

FDCD

(2)分兩種情況：依據NPDA=NAEC,ZPCD=ZACE,可得△PCDs/iACE,即可得到——=——,進而得到

AECE

5/PBBE

PD=—V34；依據NABD=NPBE,ZBAD=Z