1、北城中學初二數學知識點總結第一章 全等三角形一、全等三角形的性質（對應角、對應邊）1.如圖所示，AC和BE相交于D，且ABDCBDCED，若ABC54，則E（ ） A.25 B.27 C.30 D.45 2.如圖2，已知ABEACD，ADE =AED，B =C，指出其他對應邊和對應角。 二、 全等三角形的判定1.（sss）如圖，已知AB = CD，AC = DB；求證：A =D2.（SAS）如圖，已知ABD和ACE中，AB = AC，AD = AE，欲證ABDACE，須補充的條件是( ) A.B =C B.D =E C.DAE =BAC D.CAD =DAC 3.（ASA）如圖，點D在AB上，

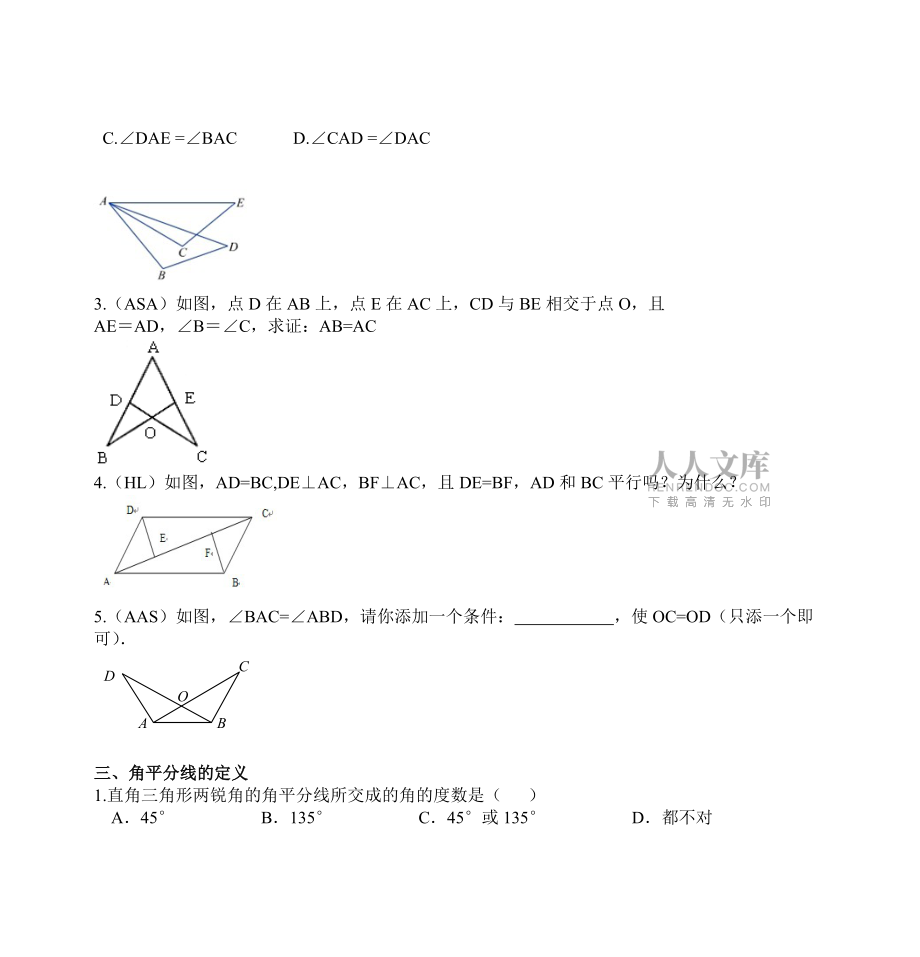
2、點E在AC上，CD與BE相交于點O，且AEAD，BC，求證：AB=AC 4.（HL）如圖，AD=BC,DEAC，BFAC，且DE=BF，AD和BC平行嗎？為什么？5.（AAS）如圖，BAC=ABD，請你添加一個條件： ，使OC=OD（只添一個即可）DOCBAB三、角平分線的定義1.直角三角形兩銳角的角平分線所交成的角的度數是（ ） A45 B135 C45或135 D都不對四、角平分線的性質1.（正定理）如圖，ABC中，C = 90，AC = BC，AD是BAC的平分線，DEAB于E，若AB = 10cm，則DBE的周長等于( ) A10cm B8cm C6cm D9cm 2.（逆定理）已知：

3、如圖，CEAB于點E，BDAC于點D，BD、CE交于點O，且BO=CO 求證：O在BAC的角平分線上第二章 軸對稱一 、軸對稱圖形及性質1.如圖，這些圖案是軸對稱圖形的是（ ） A4個 B3個 C2個 D1個二 、垂直平分線的概念及性質1.ABC中ACBC，邊AB的垂直平分線與AC交于點D，已知AC=5，BC=4，則BCD的周長是（ ） A9 B8 C7 D62.如圖，已知ABC中，AB=AC，AB的垂直平分線交AB于D，交AC于E，若ABC與EBC的周長分別是26cm、18cm，則AC=_三、 軸對稱圖形的畫法1.畫出與ABC關于x軸對稱的A1B1C1.四、 用坐標表示軸對稱1.點P（a，b

4、）是平面直角坐標系中的任意一點，則點P（a，b）關于x軸的對稱點P1的坐標是（_）； P（a，b）關于y軸的對稱點P2的坐標是（_）.五、 等腰三角形的定義及其性質應用1.已知如圖，A、D、C在一條直線上ABBDCD, C40,則ABD= . 六、等腰三角形的判定1.如圖，已知BC=CD，ABC=ADC.求證：ABD是等腰三角形.七、 等邊三角形的性質應用及判定1.如圖，D、E、F分別是等邊ABC各邊上的點，且AD=BE=CF，則DEF的形狀是（ ） A等邊三角形 B腰和底邊不相等的等腰三角形 C直角三角形 D不等邊三角形 八、 含30角的直角三角形1. 如圖，ABC中，AB=AC，BAC=1

5、20，ADBC于D，DEAB于E，試說明：BE=3AE. 第三章 實數一 、算術平方根性質：1、非負性 2、負數沒有算術平方根 3、非負數的算術平方根只有一個1.若一個正數的平方等于9，那么_，也就是說 是9的算術平方根.2.求下列各數的算術平方根： (1) (2) (3) 3.為的算術平方根，求的值.二 、平方根若x=a，那么x叫做a的平方根. 記作： 1.如果的算術平方根是7.12，那么它的平方根是_三 立方根正數的立方根是正數；0的立方根是0；負數的立方根是負數1.下列命題中正確的是（）（1）0.027的立方根是0.3；（2）不可能是負數；（3）如果a是b的立方根，那么;(4)一個數的平

6、方根與其立方根相同，則這個數是1.A.（1）（3） B.（2）（4） C.（1）（4） D.（3）(4)四、實數的分類有理數：有限小數或無限循環小數無理數：無限不循環小數數整數分數1.把下列各數分別填入相應的集合里 (1)正有理數集合： (2)有理數集合： (3)無理數集合： (4)實數集合： 五、 相反數 倒數 絕對值1.求下列各數的相反數、倒數和絕對值.(1) (2) (3) 六、實數與數軸1.如圖，數軸上表示的對應點分別為A、B，點B關于點A的對稱點為C，則點C所表示的數是（ ）A B C D七、實數的運算1.化簡：(1) (2) (3) 第四章 一次函數一、基本概念1、變量：在一個變化

7、過程中可以取不同數值的量。常量：在一個變化過程中只能取同一數值的量。例題：在勻速運動公式中,表示速度,表示時間,表示在時間內所走的路程,則變量是_,常量是_。在圓的周長公式C=2r中，變量是_，常量是_.2、函數：一般的，在一個變化過程中，如果有兩個變量x和y，并且對于x的每一個確定的值，y都有唯一確定的值與其對應，那么我們就把x稱為自變量，把y稱為因變量，y是x的函數。 *判斷Y是否為X的函數，只要看X取值確定的時候，Y是否有唯一確定的值與之對應例題：下列函數（1）y=x (2)y=2x-1 (3)y= (4)y=2-1-3x (5)y=x2-1中，是一次函數的有（ ）（A）4個 （B）3個

8、 （C）2個 （D）1個3、定義域：一般的，一個函數的自變量允許取值的范圍，叫做這個函數的定義域。4、確定函數定義域的方法： （1）關系式為整式時，函數定義域為全體實數；（2）關系式含有分式時，分式的分母不等于零； （3）關系式含有二次根式時，被開放方數大于等于零；（4）關系式中含有指數為零的式子時，底數不等于零； （5）實際問題中，函數定義域還要和實際情況相符合，使之有意義。例題：下列函數中，自變量x的取值范圍是x2的是（ ）Ay= By= Cy= Dy=函數中自變量x的取值范圍是_.已知函數，當時，y的取值范圍是 （ ）A. B. C. D.5、函數的圖像一般來說，對于一個函數，如果把自變

9、量與函數的每對對應值分別作為點的橫、縱坐標，那么坐標平面內由這些點組成的圖形，就是這個函數的圖象6、函數解析式：用含有表示自變量的字母的代數式表示因變量的式子叫做解析式。7、描點法畫函數圖形的一般步驟第一步：列表（表中給出一些自變量的值及其對應的函數值）；第二步：描點（在直角坐標系中，以自變量的值為橫坐標，相應的函數值為縱坐標，描出表格中數值對應的各點）；第三步：連線（按照橫坐標由小到大的順序把所描出的各點用平滑曲線連接起來）。8、函數的表示方法列表法：一目了然，使用起來方便，但列出的對應值是有限的，不易看出自變量與函數之間的對應規律。解析式法：簡單明了，能夠準確地反映整個變化過程中自變量與函

10、數之間的相依關系，但有些實際問題中的函數關系，不能用解析式表示。圖象法：形象直觀，但只能近似地表達兩個變量之間的函數關系。9、正比例函數及性質一般地，形如y=kx(k是常數，k0)的函數叫做正比例函數，其中k叫做比例系數.注：正比例函數一般形式 y=kx (k不為零) k不為零 x指數為1 b取零當k0時，直線y=kx經過三、一象限，從左向右上升，即隨x的增大y也增大；當k0時，圖像經過一、三象限；k0，y隨x的增大而增大；k0時，向上平移；當b0，圖象經過第一、三象限；k0，圖象經過第一、二象限；b0，y隨x的增大而增大；k0時，將直線y=kx的圖象向上平移b個單位；當b0b0經過第一、二、

11、三象限經過第一、三、四象限經過第一、三象限圖象從左到右上升，y隨x的增大而增大k0或ax+by20時x的取值范圍。第十八章勾股定理 知識點總括：1.勾股定理：如果直角三角形的兩直角邊長分別為a，b，斜邊長為c，那么 2.勾股定理逆定理：如果三角形三邊長a,b,c滿足。，那么這個三角形是直角三角形。 3.經過證明被確認正確的命題叫做定理。 我們把題設、結論正好相反的兩個命題叫做互逆命題。如果把其中一個叫做原命題，那么另一個叫做它的逆命題。（例：勾股定理與勾股定理逆定理）知識點一：利用求未知邊。如在一直角三角形中有兩邊長分別是3、4，則其第三邊長為5或（注意分類討論） ；一棵大樹離地面9米高處折斷

12、，樹頂落在離樹根底部12米遠處，求大樹折斷前的高度？答24米 知識點二：直角三角形的判定問題1、已知ABC的三邊為a、b、c，且a+b=4，ab=1，c=，試判定ABC的形狀。 2若ABC的三邊a、b、c，滿足a：b：c=1：1：，試判斷ABC的形狀。知識點三：互逆命題與互逆定理問題1、說出下列命題的逆命題，這些命題的逆命題成立嗎？同旁內角互補，兩條直線平行。如果兩個實數的平方相等，那么兩個實數平方相等。線段垂直平分線上的點到線段兩端點的距離相等。直角三角形中30角所對的直角邊等于斜邊的一半。知識點四：面積問題1、已知：如圖，四邊形ABCD，ADBC，AB=4，BC=6，CD=5，AD=3。求

13、：四邊形ABCD的面積。ACDBE第1題圖知識點五：折疊問題1、如圖，有一個直角三角形，兩條直角邊AC=6cm,BC=8cm,現將直角邊AC沿直線AD折疊，使它落在斜邊AB上，且與AE重合，你能求出CD的長嗎？2如圖，已知矩形ABCD沿著直線BD折疊，使點C落在C/處，BC/交AD于E，AD=8，AB=4，則DE的長為（ ）A3 B4 C5 D6知識點六：無理數在數軸上表示問題如圖所示：數軸上點A所表示的數為a，則a的值是（ B ）A+1 B-1 C-+1 D第十九章四邊形知識點一.平行四邊形的性質以及判定性質：1）平行四邊形兩組對邊分別平行且相等. 2）平行四邊形對角相等，鄰角互補. 3）平

14、行四邊形對角線互相平分. 4）平行四邊形是中心對稱圖形.判定方法：1）定義：兩組對邊分別平行的四邊形是平行四邊形. 2）一組對邊平行且相等的四邊形是平行四邊形. 3）兩組對邊分別相等的四邊形是平行四邊形. 4）對角線互相平分的四邊形是平行四邊形.例1、能夠判斷一個四邊形是平行四邊形的條件是（ ）A、一對角相等 B、兩條對角線互相平分階段 C、兩條對角線互相垂直 D、一組鄰角互補2如圖，平行四邊形ABCD的對角線相交于點O，直線EF經過點O，分別與AB、CD的延長線交于點E、F.求證：四邊形AECF是平行四邊形.知識點二、中心對稱圖形1）中心對稱圖形的定義以及常見的中心對稱圖形2）經過對稱中心的

15、直線一定把中心對稱圖形的面積二等分，對稱點的連線段一定經過對稱中心且被對稱中心平分.在平面內，如果一個圖形繞一個定點旋轉一定的角度后能與自身重合，那么就稱這個圖形是旋轉對稱圖形，轉動的這個角稱為這個圖形的一個旋轉角。例如：正方形繞著它的對角線的交點旋轉90后能與自身重合（如圖），所以正方形是旋轉對稱圖形，它有一個旋轉角為90。 例：下列圖形中，是旋轉對稱圖形，且有一個旋轉角為120的是 正三角形；正方形；正六邊形；正八邊形。 （寫出所有正確結論的序號）： 知識點三：三角形與梯形的中位線以及中位線定理三角形中位線:過三角形兩邊中點的線段.性質: 三角形的中位線平行且等于底邊的一半.梯形的中位線:

16、 過對邊中點的線段: 性質:梯形的中位線平行且等于上底與下底和的一半.1、如圖，在ABCD中，BD為對角線，E、F分別是ADBD的中點，連接EF若EF3，則CD的長為 (第1題)2、在梯形ABCD中，ADBC，E、F分別是BD、AC的中點，BD平分ABC。ABCDFE求證：（1）AEBD；（2）EF知識點四：矩形的性質以及判定性質：1）矩形具有平行四邊形所具有的一切性質. 2）矩形的四個角都是直角. 3）矩形的對角線相等.判定方法：1）定義：有一個角是直角的平行四邊形是矩形. 2）有三個角是直角的四邊形是矩形. 3）對角線相等的平行四邊形是矩形.定理：直角三角形斜邊上的中線等于斜邊的一半.第2

17、題例1、矩形不一定具有的特征是（ ）A、對角線相等 B、四個角是直角C、對角線互相垂直D、對邊分別相等2、如圖，矩形ABCD中，AB8，BC6，將矩形沿AC折疊，點D落在E處，且CE與AB交于F，那么AF的長是_知識點五：菱形的性質以及判定性質：1）菱形具有平行四邊形所具有的一切性質. 2）菱形的四條邊都相等. 3）菱形的對角線互相垂直并且每條對角線平分一組對角. 4）菱形的面積等于對角線乘積的一半.（如果一個四邊形的對角線互相垂直，那么這個四邊形的面積等于對角線乘積的一半）判定方法：1）定義：有一組鄰邊相等的平行四邊形是菱形 2）四條邊都相等的四邊形是菱形.例1、已知菱形ABCD的邊長為6，

18、A60，如果點P是菱形內一點，且PBPD2那么AP的長為 2若菱形兩條對角線的長分別為6和8，則這個菱形的周長為 知識點六：正方形的性質以及判定性質：1）正方形具有平行四邊形、矩形、菱形所具有的一切性質.判定方法；1）定義：有一個角是直角且有一組鄰邊相等的平行四邊形是正方形. 2）矩形+有一組鄰邊相等 3）菱形+有一個角是直角例1、正方形具有而菱形不具有的性質是（ ）A對角線互相平分 B對角線互相垂直 C對角線相等 D對角線平分一組對角2、E是正方形ABCD內一點，且EAB是等邊三角形，則ADE的度數是（ ）A70 B725 C75 D775知識點七：梯形等腰梯形的性質：等腰梯形同一底邊上的兩

19、個底角相等；等腰梯形的對角線相等.等腰梯形的判定：1）定義 2）同一底邊上兩個底角相等的梯形是等腰梯形. 3）對角線相等的梯形是等腰梯形.（其證明的方法務必掌握）關注：梯形中常見的幾種輔助線的畫法.例1 ADCBM如圖，梯形ABCD中，ADBC，點M是BC的中點，且MAMD求證：四邊形ABCD是等腰梯形2 如圖，已知在梯形ABCD中，DCAB，AD=BC，BD平分ABC，A=60（1）求ABD的度數；（2）若AD=2，求對角線BD的長第二十章數據的分析 知識點分布：1.加權平均數：加權平均數的計算公式。 權的理解:反映了某個數據在整個數據中的重要程度。學會權沒有直接給出數量，而是以比的或百分比的形式出現及頻數分布表求加權平均數的方法。2.將一組數據按照由小到大（或由大到小）的順序排列，如果數據的個數是奇數，則處于中間位置的數就是這組數據的中位數(median)；如果數據的個數是偶數，則中間兩個數據的平均數就是這組數據的中位數。 3.一組數據中出現次數最多的數據就是這組數據的眾數（mode）。 4.一組數據中的最大數據與最小數據的差叫做這組數據的極差(range)。 5.方差越大，數據的波