1、1如圖，直線y=x+c與x軸交于點A（3，0），與y軸交于點B，拋物線y=x2+bx+c經過點A，B（1）求點B的坐標和拋物線的解析式；（2）M（m，0）為x軸上一動點，過點M且垂直于x軸的直線與直線AB及拋物線分別交于點P，N點M在線段OA上運動，若以B，P，N為頂點的三角形與APM相似，求點M的坐標；點M在x軸上自由運動，若三個點M，P，N中恰有一點是其它兩點所連線段的中點（三點重合除外），則稱M，P，N三點為“共諧點”請直接寫出使得M，P，N三點成為“共諧點”的m的值2如圖1，在平面直角坐標系xOy中，拋物線C：y=ax2+bx+c與x軸相交于A，B兩點，頂點為D（0，4），AB=4，設

2、點F（m，0）是x軸的正半軸上一點，將拋物線C繞點F旋轉180°，得到新的拋物線C（1）求拋物線C的函數表達式；（2）若拋物線C與拋物線C在y軸的右側有兩個不同的公共點，求m的取值范圍（3）如圖2，P是第一象限內拋物線C上一點，它到兩坐標軸的距離相等，點P在拋物線C上的對應點P，設M是C上的動點，N是C上的動點，試探究四邊形PMPN能否成為正方形？若能，求出m的值；若不能，請說明理由3在平面直角坐標系xOy中的點P和圖形M，給出如下的定義：若在圖形M上存在一點Q，使得P、Q兩點間的距離小于或等于1，則稱P為圖形M的關聯點（1）當O的半徑為2時，在點P1（，0），P2（，），P3（，0

3、）中，O的關聯點是 點P在直線y=x上，若P為O的關聯點，求點P的橫坐標的取值范圍（2）C的圓心在x軸上，半徑為2，直線y=x+1與x軸、y軸交于點A、B若線段AB上的所有點都是C的關聯點，直接寫出圓心C的橫坐標的取值范圍4如圖，在平面直角坐標系中，拋物線y=x2+ax+b交x軸于A（1，0），B（3，0）兩點，點P是拋物線上在第一象限內的一點，直線BP與y軸相交于點C（1）求拋物線y=x2+ax+b的解析式；（2）當點P是線段BC的中點時，求點P的坐標；（3）在（2）的條件下，求sinOCB的值5如圖，拋物線y=x2+bx+c與x軸交于點A和點B，與y軸交于點C，點B坐標為（6，0），點C坐

4、標為（0，6），點D是拋物線的頂點，過點D作x軸的垂線，垂足為E，連接BD（1）求拋物線的解析式及點D的坐標；（2）點F是拋物線上的動點，當FBA=BDE時，求點F的坐標；（3）若點M是拋物線上的動點，過點M作MNx軸與拋物線交于點N，點P在x軸上，點Q在坐標平面內，以線段MN為對角線作正方形MPNQ，請寫出點Q的坐標6已知拋物線y=x2+bx3（b是常數）經過點A（1，0）（1）求該拋物線的解析式和頂點坐標；（2）P（m，t）為拋物線上的一個動點，P關于原點的對稱點為P'當點P'落在該拋物線上時，求m的值；當點P'落在第二象限內，P'A2取得最小值時，求m的值

5、7在同一直角坐標系中，拋物線C1：y=ax22x3與拋物線C2：y=x2+mx+n關于y軸對稱，C2與x軸交于A、B兩點，其中點A在點B的左側（1）求拋物線C1，C2的函數表達式；（2）求A、B兩點的坐標；（3）在拋物線C1上是否存在一點P，在拋物線C2上是否存在一點Q，使得以AB為邊，且以A、B、P、Q四點為頂點的四邊形是平行四邊形？若存在，求出P、Q兩點的坐標；若不存在，請說明理由8已知函數y=x2+（m1）x+m（m為常數）（1）該函數的圖象與x軸公共點的個數是 A.0 B.1 C.2 D.1或2（2）求證：不論m為何值，該函數的圖象的頂點都在函數y=（x+1）2的圖象上（3）當2m3時

6、，求該函數的圖象的頂點縱坐標的取值范圍9已知直線y=2x+m與拋物線y=ax2+ax+b有一個公共點M（1，0），且ab（）求拋物線頂點Q的坐標（用含a的代數式表示）；（）說明直線與拋物線有兩個交點；（）直線與拋物線的另一個交點記為N（）若1a，求線段MN長度的取值范圍；（）求QMN面積的最小值10在平面直角坐標系中，設二次函數y1=（x+a）（xa1），其中a0（1）若函數y1的圖象經過點（1，2），求函數y1的表達式；（2）若一次函數y2=ax+b的圖象與y1的圖象經過x軸上同一點，探究實數a，b滿足的關系式；（3）已知點P（x0，m）和Q（1，n）在函數y1的圖象上，若mn，求x0的取值

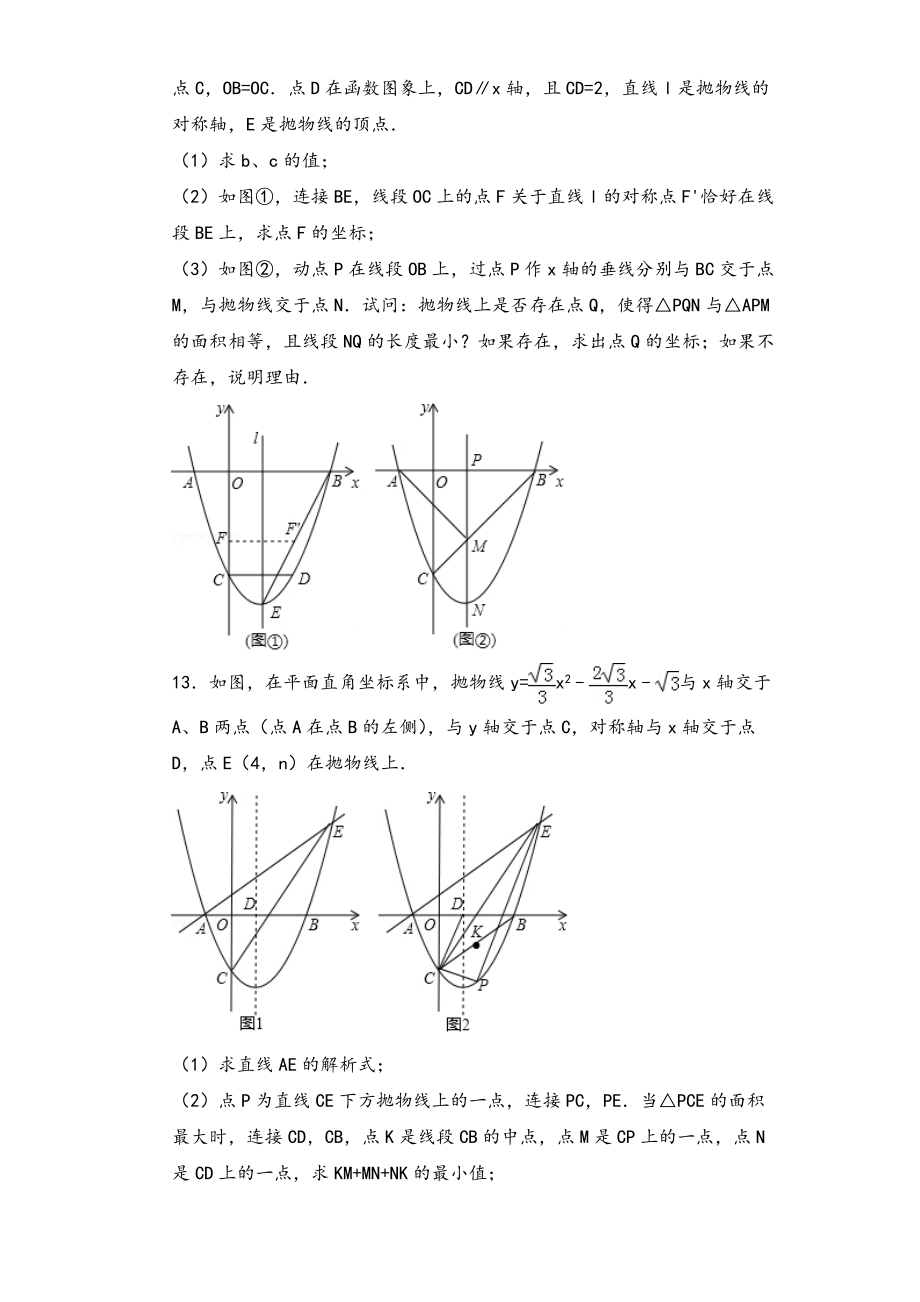
7、范圍11定義：如圖1，拋物線y=ax2+bx+c（a0）與x軸交于A，B兩點，點P在該拋物線上（P點與A、B兩點不重合），如果ABP的三邊滿足AP2+BP2=AB2，則稱點P為拋物線y=ax2+bx+c（a0）的勾股點（1）直接寫出拋物線y=x2+1的勾股點的坐標（2）如圖2，已知拋物線C：y=ax2+bx（a0）與x軸交于A，B兩點，點P（1，）是拋物線C的勾股點，求拋物線C的函數表達式（3）在（2）的條件下，點Q在拋物線C上，求滿足條件SABQ=SABP的Q點（異于點P）的坐標12如圖，二次函數y=x2+bx+c的圖象與x軸交于 A、B兩點，與y軸交于點C，OB=OC點D在函數圖象上，CD

8、x軸，且CD=2，直線l是拋物線的對稱軸，E是拋物線的頂點（1）求b、c的值；（2）如圖，連接BE，線段OC上的點F關于直線l的對稱點F'恰好在線段BE上，求點F的坐標；（3）如圖，動點P在線段OB上，過點P作x軸的垂線分別與BC交于點M，與拋物線交于點N試問：拋物線上是否存在點Q，使得PQN與APM的面積相等，且線段NQ的長度最小？如果存在，求出點Q的坐標；如果不存在，說明理由13如圖，在平面直角坐標系中，拋物線y=x2x與x軸交于A、B兩點（點A在點B的左側），與y軸交于點C，對稱軸與x軸交于點D，點E（4，n）在拋物線上（1）求直線AE的解析式；（2）點P為直線CE下方拋物線上的

9、一點，連接PC，PE當PCE的面積最大時，連接CD，CB，點K是線段CB的中點，點M是CP上的一點，點N是CD上的一點，求KM+MN+NK的最小值；（3）點G是線段CE的中點，將拋物線y=x2x沿x軸正方向平移得到新拋物線y，y經過點D，y的頂點為點F在新拋物線y的對稱軸上，是否存在點Q，使得FGQ為等腰三角形？若存在，直接寫出點Q的坐標；若不存在，請說明理由14如圖，拋物線y=ax2+bx+2經過點A（1，0），B（4，0），交y軸于點C；（1）求拋物線的解析式（用一般式表示）；（2）點D為y軸右側拋物線上一點，是否存在點D使SABC=SABD？若存在請直接給出點D坐標；若不存在請說明理由；

10、（3）將直線BC繞點B順時針旋轉45°，與拋物線交于另一點E，求BE的長15如圖，直線y=kx+b（k、b為常數）分別與x軸、y軸交于點A（4，0）、B（0，3），拋物線y=x2+2x+1與y軸交于點C（1）求直線y=kx+b的函數解析式；（2）若點P（x，y）是拋物線y=x2+2x+1上的任意一點，設點P到直線AB的距離為d，求d關于x的函數解析式，并求d取最小值時點P的坐標；（3）若點E在拋物線y=x2+2x+1的對稱軸上移動，點F在直線AB上移動，求CE+EF的最小值16如圖，已知二次函數y=x24的圖象與x軸交于A，B兩點，與y軸交于點C，C的半徑為，P為C上一動點（1）點B

11、，C的坐標分別為B（ ），C（ ）；（2）是否存在點P，使得PBC為直角三角形？若存在，求出點P的坐標；若不存在，請說明理由；（3）連接PB，若E為PB的中點，連接OE，則OE的最大值= 17已知點A（1，1）、B（4，6）在拋物線y=ax2+bx上（1）求拋物線的解析式；（2）如圖1，點F的坐標為（0，m）（m2），直線AF交拋物線于另一點G，過點G作x軸的垂線，垂足為H設拋物線與x軸的正半軸交于點E，連接FH、AE，求證：FHAE；（3）如圖2，直線AB分別交x軸、y軸于C、D兩點點P從點C出發，沿射線CD方向勻速運動，速度為每秒個單位長度；同時點Q從原點O出發，沿x軸正方向勻速運動，速度

12、為每秒1個單位長度點M是直線PQ與拋物線的一個交點，當運動到t秒時，QM=2PM，直接寫出t的值18已知直線y=kx+b與拋物線y=ax2（a0）相交于A、B兩點（點A在點B的左側），與y軸正半軸相交于點C，過點A作ADx軸，垂足為D（1）若AOB=60°，ABx軸，AB=2，求a的值；（2）若AOB=90°，點A的橫坐標為4，AC=4BC，求點B的坐標；（3）延長AD、BO相交于點E，求證：DE=CO19如圖，拋物線y=mx216mx+48m（m0）與x軸交于A，B兩點（點B在點A左側），與y軸交于點C，點D是拋物線上的一個動點，且位于第四象限，連接OD、BD、AC、AD

13、，延長AD交y軸于點E（1）若OAC為等腰直角三角形，求m的值；（2）若對任意m0，C、E兩點總關于原點對稱，求點D的坐標（用含m的式子表示）；（3）當點D運動到某一位置時，恰好使得ODB=OAD，且點D為線段AE的中點，此時對于該拋物線上任意一點P（x0，y0）總有n+4my0212y050成立，求實數n的最小值20如圖，在平面直角坐標系中，直線y=x+2與x軸交于點A，與y軸交于點C，拋物線y=x2+bx+c經過A、C兩點，與x軸的另一交點為點B（1）求拋物線的函數表達式；（2）點D為直線AC上方拋物線上一動點，連接BC、CD，設直線BD交線段AC于點E，CDE的面積為S1，BCE的面積為

14、S2，求的最大值；過點D作DFAC，垂足為點F，連接CD，是否存在點D，使得CDF中的某個角恰好等于BAC的2倍？若存在，求點D的橫坐標；若不存在，請說明理由21在平面直角坐標系xOy中，拋物線y=ax2+bx+c的開口向上，且經過點A（0，）（1）若此拋物線經過點B（2，），且與x軸相交于點E，F填空：b= （用含a的代數式表示）；當EF2的值最小時，求拋物線的解析式；（2）若a=，當0x1，拋物線上的點到x軸距離的最大值為3時，求b的值22如圖，在平面直角坐標系中，拋物線y=ax2+bx+1交y軸于點A，交x軸正半軸于點B（4，0），與過A點的直線相交于另一點D（3，），過點D作DCx軸，

15、垂足為C（1）求拋物線的表達式；（2）點P在線段OC上（不與點O、C重合），過P作PNx軸，交直線AD于M，交拋物線于點N，連接CM，求PCM面積的最大值；（3）若P是x軸正半軸上的一動點，設OP的長為t，是否存在t，使以點M、C、D、N為頂點的四邊形是平行四邊形？若存在，求出t的值；若不存在，請說明理由23如圖，拋物線y=ax2+bx3經過點A（2，3），與x軸負半軸交于點B，與y軸交于點C，且OC=3OB（1）求拋物線的解析式；（2）點D在y軸上，且BDO=BAC，求點D的坐標；（3）點M在拋物線上，點N在拋物線的對稱軸上，是否存在以點A，B，M，N為頂點的四邊形是平行四邊形？若存在，求出

16、所有符合條件的點M的坐標；若不存在，請說明理由24已知函數y=mx2（2m5）x+m2的圖象與x軸有兩個公共點（1）求m的取值范圍，并寫出當m取范圍內最大整數時函數的解析式；（2）題（1）中求得的函數記為C1當nx1時，y的取值范圍是1y3n，求n的值；函數C2：y=m（xh）2+k的圖象由函數C1的圖象平移得到，其頂點P落在以原點為圓心，半徑為的圓內或圓上設函數C1的圖象頂點為M，求點P與點M距離最大時函數C2的解析式25如圖，拋物線y=x2+x+c與x軸的負半軸交于點A，與y軸交于點B，連結AB，點C（6，）在拋物線上，直線AC與y軸交于點D（1）求c的值及直線AC的函數表達式；（2）點P

17、在x軸正半軸上，點Q在y軸正半軸上，連結PQ與直線AC交于點M，連結MO并延長交AB于點N，若M為PQ的中點求證：APMAON；設點M的橫坐標為m，求AN的長（用含m的代數式表示）26如圖，過拋物線y=x22x上一點A作x軸的平行線，交拋物線于另一點B，交y軸于點C，已知點A的橫坐標為2（1）求拋物線的對稱軸和點B的坐標；（2）在AB上任取一點P，連結OP，作點C關于直線OP的對稱點D；連結BD，求BD的最小值；當點D落在拋物線的對稱軸上，且在x軸上方時，求直線PD的函數表達式27如圖，已知拋物線y=ax2+bx+c（a0）的圖象的頂點坐標是（2，1），并且經過點（4，2），直線y=x+1與拋

18、物線交于B，D兩點，以BD為直徑作圓，圓心為點C，圓C與直線m交于對稱軸右側的點M（t，1），直線m上每一點的縱坐標都等于1（1）求拋物線的解析式；（2）證明：圓C與x軸相切；（3）過點B作BEm，垂足為E，再過點D作DFm，垂足為F，求BE：MF的值28平面直角坐標系xOy中，點A、B的橫坐標分別為a、a+2，二次函數y=x2+（m2）x+2m的圖象經過點A、B，且a、m滿足2am=d（d為常數）（1）若一次函數y1=kx+b的圖象經過A、B兩點當a=1、d=1時，求k的值；若y1隨x的增大而減小，求d的取值范圍；（2）當d=4且a2、a4時，判斷直線AB與x軸的位置關系，并說明理由；（3）

19、點A、B的位置隨著a的變化而變化，設點A、B運動的路線與y軸分別相交于點C、D，線段CD的長度會發生變化嗎？如果不變，求出CD的長；如果變化，請說明理由29如圖，拋物線y=x2+x+3與x軸交于A、B兩點（點A在點B的左側），與y軸交于點C，連接AC、BC點P沿AC以每秒1個單位長度的速度由點A向點C運動，同時，點Q沿BO以每秒2個單位長度的速度由點B向點O運動，當一個點停止運動時，另一個點也隨之停止運動，連接PQ過點Q作QDx軸，與拋物線交于點D，與BC交于點E，連接PD，與BC交于點F設點P的運動時間為t秒（t0）（1）求直線BC的函數表達式；（2）直接寫出P，D兩點的坐標（用含t的代數式

20、表示，結果需化簡）在點P、Q運動的過程中，當PQ=PD時，求t的值；（3）試探究在點P，Q運動的過程中，是否存在某一時刻，使得點F為PD的中點？若存在，請直接寫出此時t的值與點F的坐標；若不存在，請說明理由30如圖，在平面直角坐標系xOy中，拋物線y=x22x3交x軸于A，B兩點（點A在點B的左側），將該拋物線位于x軸上方曲線記作M，將該拋物線位于x軸下方部分沿x軸翻折，翻折后所得曲線記作N，曲線N交y軸于點C，連接AC、BC（1）求曲線N所在拋物線相應的函數表達式；（2）求ABC外接圓的半徑；（3）點P為曲線M或曲線N上的一動點，點Q為x軸上的一個動點，若以點B，C，P，Q為頂點的四邊形是平

21、行四邊形，求點Q的坐標31如圖，是將拋物線y=x2平移后得到的拋物線，其對稱軸為x=1，與x軸的一個交點為A（1，0），另一個交點為B，與y軸的交點為C（1）求拋物線的函數表達式；（2）若點N為拋物線上一點，且BCNC，求點N的坐標；（3）點P是拋物線上一點，點Q是一次函數y=x+的圖象上一點，若四邊形OAPQ為平行四邊形，這樣的點P、Q是否存在？若存在，分別求出點P、Q的坐標；若不存在，說明理由32如圖，已知二次函數y=ax2+bx+3（a0）的圖象經過點A（3，0），B（4，1），且與y軸交于點C，連接AB、AC、BC（1）求此二次函數的關系式；（2）判斷ABC的形狀；若ABC的外接圓記為

22、M，請直接寫出圓心M的坐標；（3）若將拋物線沿射線BA方向平移，平移后點A、B、C的對應點分別記為點A1、B1、C1，A1B1C1的外接圓記為M1，是否存在某個位置，使M1經過原點？若存在，求出此時拋物線的關系式；若不存在，請說明理由33拋物線y=4x22ax+b與x軸相交于A（x1，0），B（x2，0）（0x1x2）兩點，與y軸交于點C（1）設AB=2，tanABC=4，求該拋物線的解析式；（2）在（1）中，若點D為直線BC下方拋物線上一動點，當BCD的面積最大時，求點D的坐標；（3）是否存在整數a，b使得1x12和1x22同時成立，請證明你的結論34如圖，已知二次函數y=ax2+bx+c（

23、a0）的圖象經過A（1，0）、B（4，0）、C（0，2）三點（1）求該二次函數的解析式；（2）點D是該二次函數圖象上的一點，且滿足DBA=CAO（O是坐標原點），求點D的坐標；（3）點P是該二次函數圖象上位于第一象限上的一動點，連接PA分別交BC、y軸于點E、F，若PEB、CEF的面積分別為S1、S2，求S1S2的最大值35如圖1，拋物線y=ax2+bx+c經過平行四邊形ABCD的頂點A（0，3）、B（1，0）、D（2，3），拋物線與x軸的另一交點為E經過點E的直線l將平行四邊形ABCD分割為面積相等的兩部分，與拋物線交于另一點F點P為直線l上方拋物線上一動點，設點P的橫坐標為t（1）求拋物線

24、的解析式；（2）當t何值時，PFE的面積最大？并求最大值的立方根；（3）是否存在點P使PAE為直角三角形？若存在，求出t的值；若不存在，說明理由36如圖，某日的錢塘江觀潮信息如圖：按上述信息，小紅將“交叉潮”形成后潮頭與乙地之間的距離s（千米）與時間t（分鐘）的函數關系用圖3表示，其中：“11：40時甲地交叉潮的潮頭離乙地12千米”記為點A（0，12），點B坐標為（m，0），曲線BC可用二次函數s=t2+bt+c（b，c是常數）刻畫（1）求m的值，并求出潮頭從甲地到乙地的速度；（2）11：59時，小紅騎單車從乙地出發，沿江邊公路以0.48千米/分的速度往甲地方向去看潮，問她幾分鐘后與潮頭相遇？

25、（3）相遇后，小紅立即調轉車頭，沿江邊公路按潮頭速度與潮頭并行，但潮頭過乙地后均勻加速，而單車最高速度為0.48千米/分，小紅逐漸落后問小紅與潮頭相遇到落后潮頭1.8千米共需多長時間？（潮水加速階段速度v=v0+（t30），v0是加速前的速度）37如圖1，拋物線y=ax2+bx+2與x軸交于A，B兩點，與y軸交于點C，AB=4，矩形OBDC的邊CD=1，延長DC交拋物線于點E（1）求拋物線的解析式；（2）如圖2，點P是直線EO上方拋物線上的一個動點，過點P作y軸的平行線交直線EO于點G，作PHEO，垂足為H設PH的長為l，點P的橫坐標為m，求l與m的函數關系式（不必寫出m的取值范圍），并求出l

26、的最大值；（3）如果點N是拋物線對稱軸上的一點，拋物線上是否存在點M，使得以M，A，C，N為頂點的四邊形是平行四邊形？若存在，直接寫出所有滿足條件的點M的坐標；若不存在，請說明理由38如圖，拋物線y=x2+bx+c與直線AB交于A（4，4），B（0，4）兩點，直線AC：y=x6交y軸于點C點E是直線AB上的動點，過點E作EFx軸交AC于點F，交拋物線于點G（1）求拋物線y=x2+bx+c的表達式；（2）連接GB，EO，當四邊形GEOB是平行四邊形時，求點G的坐標；（3）在y軸上存在一點H，連接EH，HF，當點E運動到什么位置時，以A，E，F，H為頂點的四邊形是矩形？求出此時點E，H的坐標；在的

27、前提下，以點E為圓心，EH長為半徑作圓，點M為E上一動點，求AM+CM它的最小值39拋物線y=ax2+bx+3經過點A（1，0）和點B（5，0）（1）求該拋物線所對應的函數解析式；（2）該拋物線與直線y=x+3相交于C、D兩點，點P是拋物線上的動點且位于x軸下方，直線PMy軸，分別與x軸和直線CD交于點M、N連結PC、PD，如圖1，在點P運動過程中，PCD的面積是否存在最大值？若存在，求出這個最大值；若不存在，說明理由；連結PB，過點C作CQPM，垂足為點Q，如圖2，是否存在點P，使得CNQ與PBM相似？若存在，求出滿足條件的點P的坐標；若不存在，說明理由40函數的圖象與性質拓展學習片段展示：

28、【問題】如圖，在平面直角坐標系中，拋物線y=a（x2）2經過原點O，與x軸的另一個交點為A，則a= 【操作】將圖中拋物線在x軸下方的部分沿x軸折疊到x軸上方，將這部分圖象與原拋物線剩余部分的圖象組成的新圖象記為G，如圖直接寫出圖象G對應的函數解析式【探究】在圖中，過點B（0，1）作直線l平行于x軸，與圖象G的交點從左至右依次為點C，D，E，F，如圖求圖象G在直線l上方的部分對應的函數y隨x增大而增大時x的取值范圍【應用】P是圖中圖象G上一點，其橫坐標為m，連接PD，PE直接寫出PDE的面積不小于1時m的取值范圍1如圖1，經過原點O的拋物線y=ax2+bx（a0）與x軸交于另一點A（，0），在第

29、一象限內與直線y=x交于點B（2，t）（1）求這條拋物線的表達式；（2）在第四象限內的拋物線上有一點C，滿足以B，O，C為頂點的三角形的面積為2，求點C的坐標；（3）如圖2，若點M在這條拋物線上，且MBO=ABO，在（2）的條件下，是否存在點P，使得POCMOB？若存在，求出點P的坐標；若不存在，請說明理由2如圖，在平面直角坐標系中，二次函數y=x2+bx+c的圖象與坐標軸交于A，B，C三點，其中點A的坐標為（3，0），點B的坐標為（4，0），連接AC，BC動點P從點A出發，在線段AC上以每秒1個單位長度的速度向點C作勻速運動；同時，動點Q從點O出發，在線段OB上以每秒1個單位長度的速度向點B

30、作勻速運動，當其中一點到達終點時，另一點隨之停止運動，設運動時間為t秒連接PQ（1）填空：b= ，c= ；（2）在點P，Q運動過程中，APQ可能是直角三角形嗎？請說明理由；（3）在x軸下方，該二次函數的圖象上是否存在點M，使PQM是以點P為直角頂點的等腰直角三角形？若存在，請求出運動時間t；若不存在，請說明理由；（4）如圖，點N的坐標為（，0），線段PQ的中點為H，連接NH，當點Q關于直線NH的對稱點Q恰好落在線段BC上時，請直接寫出點Q的坐標3定義：對于給定的兩個函數，任取自變量x的一個值，當x0時，它們對應的函數值互為相反數；當x0時，它們對應的函數值相等，我們稱這樣的兩個函數互為相關函數

31、例如：一次函數y=x1，它的相關函數為y=（1）已知點A（5，8）在一次函數y=ax3的相關函數的圖象上，求a的值；（2）已知二次函數y=x2+4x當點B（m，）在這個函數的相關函數的圖象上時，求m的值；當3x3時，求函數y=x2+4x的相關函數的最大值和最小值；（3）在平面直角坐標系中，點M，N的坐標分別為（，1），（，1），連結MN直接寫出線段MN與二次函數y=x2+4x+n的相關函數的圖象有兩個公共點時n的取值范圍4如圖，在平面直角坐標系xOy中，已知A，B兩點的坐標分別為（4，0），（4，0），C（m，0）是線段A B上一點（與 A，B點不重合），拋物線L1：y=ax2+b1x+c1（

32、a0）經過點A，C，頂點為D，拋物線L2：y=ax2+b2x+c2（a0）經過點C，B，頂點為E，AD，BE的延長線相交于點F（1）若a=，m=1，求拋物線L1，L2的解析式；（2）若a=1，AFBF，求m的值；（3）是否存在這樣的實數a（a0），無論m取何值，直線AF與BF都不可能互相垂直？若存在，請直接寫出a的兩個不同的值；若不存在，請說明理由5如圖，已知拋物線y=ax22ax9a與坐標軸交于A，B，C三點，其中C（0，3），BAC的平分線AE交y軸于點D，交BC于點E，過點D的直線l與射線AC，AB分別交于點M，N（1）直接寫出a的值、點A的坐標及拋物線的對稱軸；（2）點P為拋物線的對稱

33、軸上一動點，若PAD為等腰三角形，求出點P的坐標；（3）證明：當直線l繞點D旋轉時，+均為定值，并求出該定值6如圖1，矩形OABC的頂點A，C的坐標分別為（4，0），（0，6），直線AD交B C于點D，tanOAD=2，拋物線M1：y=ax2+bx（a0）過A，D兩點（1）求點D的坐標和拋物線M1的表達式；（2）點P是拋物線M1對稱軸上一動點，當CPA=90°時，求所有符合條件的點P的坐標；（3）如圖2，點E（0，4），連接AE，將拋物線M1的圖象向下平移m（m0）個單位得到拋物線M2設點D平移后的對應點為點D，當點D恰好在直線AE上時，求m的值；當1xm（m1）時，若拋物線M2與直

34、線AE有兩個交點，求m的取值范圍7如圖，已知拋物線y=ax2+2x+c與y軸交于點A（0，6），與x軸交于點B（6，0），點P是線段AB上方拋物線上的一個動點（1）求這條拋物線的表達式及其頂點坐標；（2）當點P移動到拋物線的什么位置時，使得PAB=75°，求出此時點P的坐標；（3）當點P從A點出發沿線段AB上方的拋物線向終點B移動，在移動中，點P的橫坐標以每秒1個單位長度的速度變動；與此同時點M以每秒1個單位長度的速度沿AO向終點O移動，點P，M移動到各自終點時停止當兩個動點移動t秒時，求四邊形PAMB的面積S關于t的函數表達式，并求t為何值時，S有最大值，最大值是多少？8如圖，直線

35、y=x+分別與x軸、y軸交于B、C兩點，點A在x軸上，ACB=90°，拋物線y=ax2+bx+經過A，B兩點（1）求A、B兩點的坐標；（2）求拋物線的解析式；（3）點M是直線BC上方拋物線上的一點，過點M作MHBC于點H，作MDy軸交BC于點D，求DMH周長的最大值9如圖，拋物線y=ax2+bx2的對稱軸是直線x=1，與x軸交于A，B兩點，與y軸交于點C，點A的坐標為（2，0），點P為拋物線上的一個動點，過點P作PDx軸于點D，交直線BC于點E（1）求拋物線解析式；（2）若點P在第一象限內，當OD=4PE時，求四邊形POBE的面積；（3）在（2）的條件下，若點M為直線BC上一點，點N

36、為平面直角坐標系內一點，是否存在這樣的點M和點N，使得以點B，D，M，N為頂點的四邊形是菱形？若存在，直接寫出點N的坐標；若不存在，請說明理由【溫馨提示：考生可以根據題意，在備用圖中補充圖形，以便探究】10如圖，拋物線y=x2+bx+c與x軸分別交于A（1，0），B（5，0）兩點（1）求拋物線的解析式；（2）在第二象限內取一點C，作CD垂直X軸于點D，鏈接AC，且AD=5，CD=8，將RtACD沿x軸向右平移m個單位，當點C落在拋物線上時，求m的值；（3）在（2）的條件下，當點C第一次落在拋物線上記為點E，點P是拋物線對稱軸上一點試探究：在拋物線上是否存在點Q，使以點B、E、P、Q為頂點的四邊

37、形是平行四邊形？若存在，請出點Q的坐標；若不存在，請說明理由11如圖，已知拋物線y=ax2+bx+c過點A（1，0），B（3，0），C（0，3），點M、N為拋物線上的動點，過點M作MDy軸，交直線BC于點D，交x軸于點E（1）求二次函數y=ax2+bx+c的表達式；（2）過點N作NFx軸，垂足為點F，若四邊形MNFE為正方形（此處限定點M在對稱軸的右側），求該正方形的面積；（3）若DMN=90°，MD=MN，求點M的橫坐標12如圖1，已知二次函數y=ax2+bx+c（a、b、c為常數，a0）的圖象過點O（0，0）和點A（4，0），函數圖象最低點M的縱坐標為，直線l的解析式為y=x（1

38、）求二次函數的解析式；（2）直線l沿x軸向右平移，得直線l，l與線段OA相交于點B，與x軸下方的拋物線相交于點C，過點C作CEx軸于點E，把BCE沿直線l折疊，當點E恰好落在拋物線上點E時（圖2），求直線l的解析式；（3）在（2）的條件下，l與y軸交于點N，把BON繞點O逆時針旋轉135°得到BON，P為l上的動點，當PBN為等腰三角形時，求符合條件的點P的坐標13如圖，矩形OABC的兩邊在坐標軸上，點A的坐標為（10，0），拋物線y=ax2+bx+4過點B，C兩點，且與x軸的一個交點為D（2，0），點P是線段CB上的動點，設CP=t（0t10）（1）請直接寫出B、C兩點的坐標及拋物

39、線的解析式；（2）過點P作PEBC，交拋物線于點E，連接BE，當t為何值時，PBE=OCD？（3）點Q是x軸上的動點，過點P作PMBQ，交CQ于點M，作PNCQ，交BQ于點N，當四邊形PMQN為正方形時，請求出t的值14如圖所示，在平面直角坐標系中，C經過坐標原點O，且與x軸，y軸分別相交于M（4，0），N（0，3）兩點已知拋物線開口向上，與C交于N，H，P三點，P為拋物線的頂點，拋物線的對稱軸經過點C且垂直x軸于點D（1）求線段CD的長及頂點P的坐標；（2）求拋物線的函數表達式；（3）設拋物線交x軸于A，B兩點，在拋物線上是否存在點Q，使得S四邊形OPMN=8SQAB，且QABOBN成立？若

40、存在，請求出Q點的坐標；若不存在，請說明理由15如圖，在平面直角坐標系中，拋物線y=ax2+bx+c（a0）與y軸交與點C（0，3），與x軸交于A、B兩點，點B坐標為（4，0），拋物線的對稱軸方程為x=1（1）求拋物線的解析式；（2）點M從A點出發，在線段AB上以每秒3個單位長度的速度向B點運動，同時點N從B點出發，在線段BC上以每秒1個單位長度的速度向C點運動，其中一個點到達終點時，另一個點也停止運動，設MBN的面積為S，點M運動時間為t，試求S與t的函數關系，并求S的最大值；（3）在點M運動過程中，是否存在某一時刻t，使MBN為直角三角形？若存在，求出t值；若不存在，請說明理由16已知拋物

41、線y=ax2+bx+c，其中2a=b0c，且a+b+c=0（1）直接寫出關于x的一元二次方程ax2+bx+c=0的一個根；（2）證明：拋物線y=ax2+bx+c的頂點A在第三象限；（3）直線y=x+m與x，y軸分別相交于B，C兩點，與拋物線y=ax2+bx+c相交于A，D兩點設拋物線y=ax2+bx+c的對稱軸與x軸相交于E如果在對稱軸左側的拋物線上存在點F，使得ADF與BOC相似，并且SADF=SADE，求此時拋物線的表達式17已知二次函數y=x2+bx+c+1，當b=1時，求這個二次函數的對稱軸的方程； 若c=b22b，問：b為何值時，二次函數的圖象與x軸相切？若二次函數的圖象與x軸交于點

42、A（x1，0），B（x2，0），且x1x2，b0，與y軸的正半軸交于點M，以AB為直徑的半圓恰好過點M，二次函數的對稱軸l與x軸、直線BM、直線AM分別交于點D、E、F，且滿足=，求二次函數的表達式18如圖1，點A坐標為（2，0），以OA為邊在第一象限內作等邊OAB，點C為x軸上一動點，且在點A右側，連接BC，以BC為邊在第一象限內作等邊BCD，連接AD交BC于E（1）直接回答：OBC與ABD全等嗎？試說明：無論點C如何移動，AD始終與OB平行；（2）當點C運動到使AC2=AEAD時，如圖2，經過O、B、C三點的拋物線為y1試問：y1上是否存在動點P，使BEP為直角三角形且BE為直角邊？若存在

43、，求出點P坐標；若不存在，說明理由；（3）在（2）的條件下，將y1沿x軸翻折得y2，設y1與y2組成的圖形為M，函數y=x+m的圖象l與M有公共點試寫出：l與M的公共點為3個時，m的取值19拋物線y=x2+bx+c與x軸交于A（1，0），B（m，0），與y軸交于C（1）若m=3，求拋物線的解析式，并寫出拋物線的對稱軸；（2）如圖1，在（1）的條件下，設拋物線的對稱軸交x軸于D，在對稱軸左側的拋物線上有一點E，使SACE=SACD，求點E的坐標；（3）如圖2，設F（1，4），FGy于G，在線段OG上是否存在點P，使OBP=FPG？若存在，求m的取值范圍；若不存在，請說明理由20在平面直角坐標系x

44、Oy中，規定：拋物線y=a（xh）2+k的伴隨直線為y=a（xh）+k例如：拋物線y=2（x+1）23的伴隨直線為y=2（x+1）3，即y=2x1（1）在上面規定下，拋物線y=（x+1）24的頂點坐標為 ，伴隨直線為 ，拋物線y=（x+1）24與其伴隨直線的交點坐標為 和 ；（2）如圖，頂點在第一象限的拋物線y=m（x1）24m與其伴隨直線相交于點A，B（點A在點B的左側），與x軸交于點C，D若CAB=90°，求m的值；如果點P（x，y）是直線BC上方拋物線上的一個動點，PBC的面積記為S，當S取得最大值時，求m的值21我們知道，經過原點的拋物線可以用y=ax2+bx（a0）表示，對

45、于這樣的拋物線：（1）當拋物線經過點（2，0）和（1，3）時，求拋物線的表達式；（2）當拋物線的頂點在直線y=2x上時，求b的值；（3）如圖，現有一組這樣的拋物線，它們的頂點A1、A2、，An在直線y=2x上，橫坐標依次為1，2，3，n（n為正整數，且n12），分別過每個頂點作x軸的垂線，垂足記為B1、B2，Bn，以線段AnBn為邊向左作正方形AnBnCnDn，如果這組拋物線中的某一條經過點Dn，求此時滿足條件的正方形AnBnCnDn的邊長22如圖，拋物線y=a（x1）（x3）與x軸交于A，B兩點，與y軸的正半軸交于點C，其頂點為D（1）寫出C，D兩點的坐標（用含a的式子表示）；（2）設SBC

46、D：SABD=k，求k的值；（3）當BCD是直角三角形時，求對應拋物線的解析式23如圖所示，頂點為（，）的拋物線y=ax2+bx+c過點M（2，0）（1）求拋物線的解析式；（2）點A是拋物線與x軸的交點（不與點M重合），點B是拋物線與y軸的交點，點C是直線y=x+1上一點（處于x軸下方），點D是反比例函數y=（k0）圖象上一點，若以點A，B，C，D為頂點的四邊形是菱形，求k的值 24如圖，拋物線y=ax2+bx2與x軸交于A、B兩點，與y軸交于C點，已知A（3，0），且M（1，）是拋物線上另一點（1）求a、b的值；（2）連結AC，設點P是y軸上任一點，若以P、A、C三點為頂點的三角形是等腰三角

47、形，求P點的坐標；（3）若點N是x軸正半軸上且在拋物線內的一動點（不與O、A重合），過點N作NHAC交拋物線的對稱軸于H點設ON=t，ONH的面積為S，求S與t之間的函數關系式25如圖1，在平面直角坐標系中，已知拋物線y=ax2+bx5與x軸交于A（1，0），B（5，0）兩點，與y軸交于點C（1）求拋物線的函數表達式；（2）若點D是y軸上的一點，且以B，C，D為頂點的三角形與ABC相似，求點D的坐標；（3）如圖2，CEx軸與拋物線相交于點E，點H是直線CE下方拋物線上的動點，過點H且與y軸平行的直線與BC，CE分別相交于點F，G，試探究當點H運動到何處時，四邊形CHEF的面積最大，求點H的坐標

48、及最大面積；（4）若點K為拋物線的頂點，點M（4，m）是該拋物線上的一點，在x軸，y軸上分別找點P，Q，使四邊形PQKM的周長最小，求出點P，Q的坐標26如圖，拋物線y=x2+bx+c經過點B（3，0），C（0，2），直線l：y=x交y軸于點E，且與拋物線交于A，D兩點，P為拋物線上一動點（不與A，D重合）（1）求拋物線的解析式；（2）當點P在直線l下方時，過點P作PMx軸交l于點M，PNy軸交l于點N，求PM+PN的最大值（3）設F為直線l上的點，以E，C，P，F為頂點的四邊形能否構成平行四邊形？若能，求出點F的坐標；若不能，請說明理由27如圖，M的圓心M（1，2），M經過坐標原點O，與y軸

49、交于點A經過點A的一條直線l解析式為：y=x+4與x軸交于點B，以M為頂點的拋物線經過x軸上點D（2，0）和點C（4，0）（1）求拋物線的解析式；（2）求證：直線l是M的切線；（3）點P為拋物線上一動點，且PE與直線l垂直，垂足為E；PFy軸，交直線l于點F，是否存在這樣的點P，使PEF的面積最小若存在，請求出此時點P的坐標及PEF面積的最小值；若不存在，請說明理由28如圖，在平面直角坐標系中，矩形OABC的邊OA、OC分別在x軸、y軸上，點B坐標為（4，t）（t0），二次函數y=x2+bx（b0）的圖象經過點B，頂點為點D（1）當t=12時，頂點D到x軸的距離等于 ；（2）點E是二次函數y=

50、x2+bx（b0）的圖象與x軸的一個公共點（點E與點O不重合），求OEEA的最大值及取得最大值時的二次函數表達式；（3）矩形OABC的對角線OB、AC交于點F，直線l平行于x軸，交二次函數y=x2+bx（b0）的圖象于點M、N，連接DM、DN，當DMNFOC時，求t的值29如圖甲，直線y=x+3與x軸、y軸分別交于點B、點C，經過B、C兩點的拋物線y=x2+bx+c與x軸的另一個交點為A，頂點為P（1）求該拋物線的解析式；（2）在該拋物線的對稱軸上是否存在點M，使以C，P，M為頂點的三角形為等腰三角形？若存在，請直接寫出所符合條件的點M的坐標；若不存在，請說明理由；（3）當0x3時，在拋物線上

51、求一點E，使CBE的面積有最大值（圖乙、丙供畫圖探究）30如圖，拋物線y=ax2+bx+c（a0）與直線y=x+1相交于A（1，0），B（4，m）兩點，且拋物線經過點C（5，0）（1）求拋物線的解析式；（2）點P是拋物線上的一個動點（不與點A、點B重合），過點P作直線PDx軸于點D，交直線AB于點E當PE=2ED時，求P點坐標；是否存在點P使BEC為等腰三角形？若存在請直接寫出點P的坐標；若不存在，請說明理由1如圖，直線y=x+c與x軸交于點A（3，0），與y軸交于點B，拋物線y=x2+bx+c經過點A，B（1）求點B的坐標和拋物線的解析式；（2）M（m，0）為x軸上一動點，過點M且垂直于x軸

52、的直線與直線AB及拋物線分別交于點P，N點M在線段OA上運動，若以B，P，N為頂點的三角形與APM相似，求點M的坐標；點M在x軸上自由運動，若三個點M，P，N中恰有一點是其它兩點所連線段的中點（三點重合除外），則稱M，P，N三點為“共諧點”請直接寫出使得M，P，N三點成為“共諧點”的m的值【分析】（1）把A點坐標代入直線解析式可求得c，則可求得B點坐標，由A、B的坐標，利用待定系數法可求得拋物線解析式；（2）由M點坐標可表示P、N的坐標，從而可表示出MA、MP、PN、PB的長，分NBP=90°和BNP=90°兩種情況，分別利用相似三角形的性質可得到關于m的方程，可求得m的值

53、；用m可表示出M、P、N的坐標，由題意可知有P為線段MN的中點、M為線段PN的中點或N為線段PM的中點，可分別得到關于m的方程，可求得m的值【解答】解：（1）y=x+c與x軸交于點A（3，0），與y軸交于點B，0=2+c，解得c=2，B（0，2），拋物線y=x2+bx+c經過點A，B，解得，拋物線解析式為y=x2+x+2；（2）由（1）可知直線解析式為y=x+2，M（m，0）為x軸上一動點，過點M且垂直于x軸的直線與直線AB及拋物線分別交于點P，N，P（m，m+2），N（m，m2+m+2），PM=m+2，AM=3m，PN=m2+m+2（m+2）=m2+4m，BPN和APM相似，且BPN=APM

54、，BNP=AMP=90°或NBP=AMP=90°，當BNP=90°時，則有BNMN，N點的縱坐標為2，m2+m+2=2，解得m=0（舍去）或m=2.5，M（2.5，0）；當NBP=90°時，過點N作NCy軸于點C，則NBC+BNC=90°，NC=m，BC=m2+m+22=m2+m，NBP=90°，NBC+ABO=90°，ABO=NBC，RtNCBRtBOA，=，=，解得m=0（舍去）或m=，M（，0）；綜上可知當以B，P，N為頂點的三角形與APM相似時，點M的坐標為（2.5，0）或（，0）；由可知M（m，0），P（m，m+2），N（m，m2+m+2），M，P，N三點為“共諧點”，有P為線段MN的中點、M為線段PN的中點或N為線段PM的中點，當P為線段MN的中點時，則有2（m+2）=m2+m+2，解得m=3（三點重合，舍去）或m=；當M為線段PN的中點時，則有m+2+（m2+m+2）=0，解得m=3（舍去）或m=1；當N為線段PM的中點時，則有m+2=2（m2+m+2），解得m=3（舍去）或m=；綜上可知當M，P，