1、精選優質文檔-傾情為你奉上二面角大小的幾種求法二面角大小的求法中知識的綜合性較強，方法的靈活性較大，一般而言，二面角的大小往往轉化為其平面角的大小，從而又化歸為三角形的內角大小，在其求解過程中，主要是利用平面幾何、立體幾何、三角函數等重要知識。求二面角大小的關鍵是，根據不同問題給出的幾何背景，恰在此時當選擇方法，作出二面角的平面角，有時亦可直接運用射影面積公式求出二面角的大小。I. 尋找有棱二面角的平面角的方法 ( 定義法、三垂線法、垂面法、射影面積法 )一、定義法：利用二面角的平面角的定義，在二面角的棱上取一點（特殊點），過該點在兩個半平面內作垂直于棱的射線，兩射線所成的角就是二面角的平面角

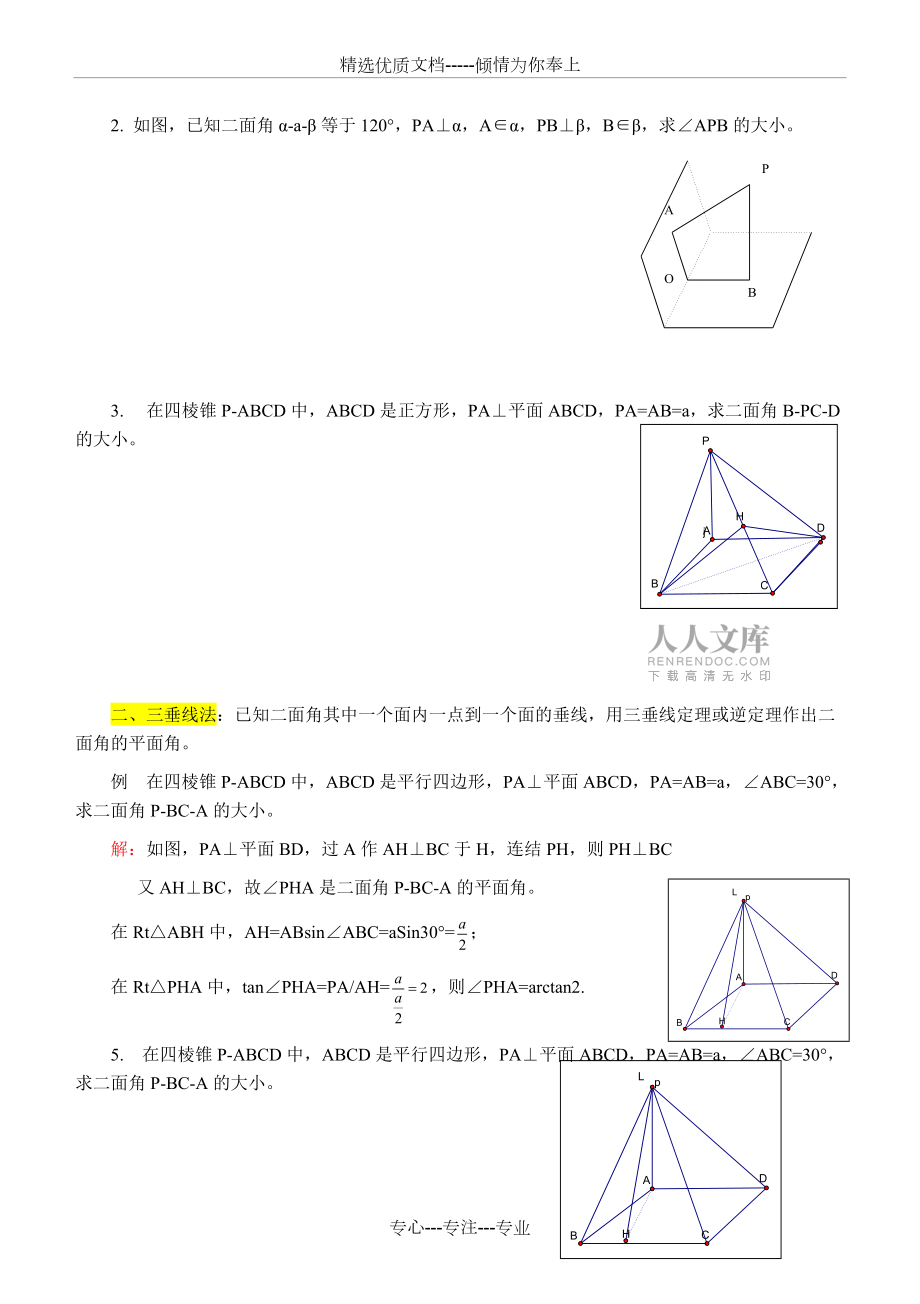
2、，這是一種最基本的方法。要注意用二面角的平面角定義的三個“主要特征”來找出平面角。PBCAEFD例 空間三條射線CA、CP、CB，PCA=PCB=60o，ACB=90o，求二面角B-PC-A的大小。解：過PC上的點D分別作DEAC于E，DFBC于F，連EF.EDF為二面角B-PC-A的平面角，設CD=a，PCA=PCB=600，CE=CF=2a，DE=DF=，又ACB=900，EF=，EDF=1. 在三棱錐P-ABC中，APB=BPC=CPA=600，求二面角A-PB-C的余弦值。ABCNMPQ2. 如圖，已知二面角-等于120，PA，A，PB，B，求APB的大小。POBA 3. 在四棱錐P-

3、ABCD中，ABCD是正方形，PA平面ABCD，PA=AB=a，求二面角B-PC-D的大小。二、三垂線法：已知二面角其中一個面內一點到一個面的垂線，用三垂線定理或逆定理作出二面角的平面角。例 在四棱錐P-ABCD中，ABCD是平行四邊形，PA平面ABCD，PA=AB=a，ABC=30，求二面角P-BC-A的大小。解：如圖，PA平面BD，過A作AHBC于H，連結PH，則PHBC 又AHBC，故PHA是二面角P-BC-A的平面角。在RtABH中，AH=ABsinABC=aSin30=；在RtPHA中，tanPHA=PA/AH=，則PHA=arctan2.5. 在四棱錐P-ABCD中，ABCD是平行

4、四邊形，PA平面ABCD，PA=AB=a，ABC=30，求二面角P-BC-A的大小。CBMBAPNK6. 如圖，在三棱錐P-ABC中，PA平面ABC，PA=AB，AC=BC=1，ACB=900，M是PB的中點。(1)求證：BCPC，(2)平面MAC與平面ABC所成的二面角的正切。7. ABC中，A=90，AB=4，AC=3，平面ABC外一點P在平面ABC內的射影是AB中點M，二面角PACB的大小為45。求（1）二面角PBCA的大小；（2）二面角CPBA的大小。CDPMBA8. 如圖，已知ABC中，ABBC，S為平面ABC外的一點，SA平面ABC，AMSB于M，ANSC于N,(1)求證平面SAB

5、平面SBC (2)求證ANM是二面角ASCB的平面角.ABCMNS9. 第8題的變式：如上圖，已知ABC中，ABBC，S為平面ABC外的一點，SA平面ABC，ACB600，SAACa，(1)求證平面SAB平面SBC (2)求二面角ASCBC的正弦值.ABCDA1B1C1D1EO10. 如圖,ABCD-A1B1C1D1是長方體，側棱AA1長為1，底面為正方體且邊長為2，E是棱BC的中點，求面C1DE與面CDE所成二面角的正切值。11. 如圖4，平面平面，=l，A，B，點A在直線l上的射影為A1，點B在l的射影為B1，已知AB=2，AA1=1，BB1=，求：二面角A1ABB1的大小。圖4B1AA1

6、BL EF三、垂面法：已知二面角內一點到兩個面的垂線時，過兩垂線作平面與兩個半平面的交線所成的角即為平面角，由此可知，二面角的平面角所在的平面與棱垂直。例 在四棱錐P-ABCD中，ABCD是正方形，PA平面ABCD，PA=AB=a，求B-PC-D的大小。解：（垂面法）如圖，PA平面BDBDAC BDBC過BD作平面BDHPC于HPCDH、BH BHD為二面角B-PC-D的平面角。因PB=a,BC=a,PC=a,PBBC=SPBC=PCBH則BH=DH，又BD=在BHD中由余弦定理，得：cosBHD，又0BHD ，則BHD=，二面角B-PC-D的大小是。PlCBA12. 空間的點P到二面角的面、

7、及棱l的距離分別為4、3、，求二面角的大小.ABCSD13如圖，在三棱錐SABC中，SA底面ABC，ABBC，DE垂直平分SC且分別交AC、SC于D、E，又SAAB，SBBC，求二面角EBDC的度數。II. 尋找無棱二面角的平面角的方法 ( 射影面積法、平移或延長(展)線(面)法 )四、射影面積法：利用面積射影公式S射S原cos,其中為平面角的大小，此方法不必在圖形中畫出平面角。例 在四棱錐P-ABCD中，ABCD為正方形，PA平面ABCD，PAABa，求平面PBA與平面PDC所成二面角的大小。解：（面積法）如圖，同時，BC平面BPA于B ，故PBA是PCD在平面PBA上的射影設平面PBA與平

8、面PDC所成二面角大小為，則cos= =45AHMD1C1B1A1BCD14. 如圖，設M為正方體ABCD-A1B1C1D1的棱CC1的中點，求平面BMD1與底面ABCD所成的二面角的大小。 15. 如圖，與所成的角為600，于C，于B，AC3，BD4，CD2，求A、B兩點間的距離。AlDCAlBCEBD五、平移或延長（展）線（面）法：對于一類沒有給出棱的二面角，應先延伸兩個半平面，使之相交出現棱，然后再選用上述方法（尤其要考慮射影法）。例 在四棱錐P-ABCD中，ABCD為正方形，PA平面ABCD，PAABa，求平面PBA與平面PDC所成二面角的大小。（補形化為定義法）解：（補形化為定義法）

9、如圖，將四棱錐P-ABCD補形得正方體ABCD-PQMN，則PQPA、PD，于是APD是兩面所成二面角的平面角。在RtPAD中，PA=AD，則APD=45。即平面BAP與平面PDC所成二面角的大小為4516. 在四棱錐P-ABCD中，ABCD為正方形，PA平面ABCD，PAABa，求平面PBA與平面PDC所成二面角的大小。六、向量法解立體幾何中是一種十分簡捷的也是非常傳統的解法，可以說所有的立體幾何題都可以用向量法求解，用向量法解立體幾何題時，通常要建立空間直角坐標系，寫出各點的坐標，然后將幾何圖中的線段寫成用坐標法表示的向量，進行向量計算解題。例（2009天津卷理）如圖，在五面體ABCDEF

10、中，FA 平面ABCD, AD/BC/FE，ABAD，M為EC的中點，AF=AB=BC=FE=AD。,(I)求異面直線BF與DE所成的角的大小；(II) 證明平面AMD平面CDE；(III)求二面角A-CD-E的余弦值。 解：如圖所示，建立空間直角坐標系，以點為坐標原點。設依題意得 （I） 所以異面直線與所成的角的大小為.（II）證明： ， （III） 又由題設，平面的一個法向量為18.（2008湖北）如圖，在直三棱柱中，平面側面.(I) 求證：；(II) 若直線與平面所成的角為,二面角的大小為，試判斷與的大小關系，并予以證明.分析：由已知條件可知：平面ABB1 A1平面BCC1 B1平面AB

11、C于是很容易想到以B 點為空間坐標原點建立坐標系，并將相關線段寫成用坐標表示的向量，先求出二面角的兩個半平面的法向量，再利用兩向量夾角公式求解。（答案：，且）由此可見，二面角的類型和求法可用框圖展現如下：分析：所求二面角與底面ABC所在的位置無關，故不妨利用定義求解。略解：在二面角的棱PB上任取一點Q，在半平面PBA和半平面PBC上作QMPB，QNPB，則由定義可得MQN即為二面角的平面角。設PM=a,則在RtPQM和RtPQN中可求得QM=QN=a；又由PQNPQM得PN=a,故在正三角形PMN中MN=a,在三角形MQN中由余弦定理得cosMQN=，即二面角的余弦值為。因為AB=AD=a，。

12、過B作BHPC于H，連結DHDHPC故BHD為二面角B-PC-D的平面角。因PB=a,BC=a,PC=a,PBBC=SPBC=PCBH，則BH=DH又BD=。在BHD中由余弦定理，得：cosBHD，又0BHD 則BHD=，二面角B-PC-D的大小是。基礎練習1 二面角是指（ ）A 兩個平面相交所組成的圖形B 一個平面繞這個平面內一條直線旋轉所組成的圖形C 從一個平面內的一條直線出發的一個半平面與這個平面所組成的圖形D 從一條直線出發的兩個半平面所組成的圖形2平面與平面、都相交，則這三個平面可能有（ ） A 1條或2條交線 B 2條或3條交線C 僅2條交線 D 1條或2條或3條交線3在300的二

13、面角的一個面內有一個點，若它到另一個面的距離是10，則它到棱的距離是( ) A 5 B 20 C D4在直二面角-l-中，RtABC在平面內，斜邊BC在棱l上，若AB與面所成的角為600，則AC與平面所成的角為（ ） ABCD A 300 B 450 C 600 D 12005如圖，射線BD、BA、BC兩兩互相垂直，AB=BC=1，BD=，則弧度數為的二面角是（ ） A. D-AC-B B. A-CD-B C. A-BC-D D. A-BD-C6ABC在平面的射影是A1B1C1，如果ABC所在平面和平面成角，有( ) A. SA1B1C1=SABCsin B. SA1B1C1= SABCcos

14、C. SABC =SA1B1C1sin D. SABC =SA1B1C1cosABMNPl7如圖，若P為二面角M-l-N的面N內一點，PBl，B為垂足，A為l上一點，且PAB=，PA與平面M所成角為，二面角M-l-N的大小為，則有（ ） Asin=sinsin Bsin=sinsinC sin=sinsin D 以上都不對8在600的二面角的棱上有兩點A、B，AC、BD分別是在這個二面角的兩個面內垂直于AB的線段，已知：AB=6，AC=3，BD=4，則CD= 。9已知ABC和平面，A=300，B=600，AB=2，AB，且平面ABC與所成角為300，則點C到平面的距離為 。10正方體ABCDA

15、1B1C1D1中，平面AA1C1C和平面A1BCD1所成的二面角（銳角）為 。11已知菱形的一個內角是600，邊長為a，沿菱形較短的對角線折成大小為600的二面角，則菱形中含600角的兩個頂點間的距離為 。ABC1C12如圖，ABC在平面內的射影為ABC1，若ABC1=，BC1=a，且平面ABC與平面所成的角為，求點C到平面的距離13在二面角-AB-的一個平面內，有一直線AC，它與棱AB成450角，AC與平面成300角，求二面角-AB-的度數。 深化練習14若二面角內一點到二面角的兩個面的距離分別為a和，到棱的距離為2a，則此二面角的度數是 。15把等腰直角三角形ABC沿斜邊BC上的高AD折成一個二面角，若BAC=600，則此二面角的度數是 。AFEBDC16如