1、直線與平面平行的判定教學設計教材：人教A版必修二執教人：劉戰獻學校：安順二中2019年6月10日“直線與平面平行的判定”教學設計授課教師：劉戰獻 學校：安順二中一、教學目標與要求1. 知識與技能：理解并掌握直線與平面平行的判定定理；能應用定理證明簡單的線面平行問題.2. 過程與方法：通過直感知-操作確認-思辨論證的認識方法，經歷直線與平面平行的判定定理的發現過程，培養學生合情推理能力，進一步滲透化歸和轉化的數學思想，滲透立體幾何將空間問題降維為平面問題的一般方法. 初步掌握立體幾何中的三種語言的應用，并培養學生的觀察、探究、發現能力和空間想象能力、邏輯思維能力.3. 情感態度與價值觀：通過數學

2、思辨和推理過程培養學生說理、批判、質疑的嚴謹風格和理性精神；領會數學科學的應用價值，激發學生的數學學習興趣，培養學生主動探究,主動提出問題的習慣.二、教學重點與難點（一）教學重點：直線與平面平行的判定定理的理解與簡單應用.（二）教學難點：線面平行判定的應用，平行輔助線的作法三、教學過程 教學階段教學設計設計意圖復習回顧直觀感知提出問題【必備知識】（1）直線與平面的位置關系有_、_、_三種.（2）直線與平面平行的定義：直線與平面_公共點【直觀感知】（1）讓學生觀察門轉動到離開門框的任何位置時，門的邊緣線始終與門框所在的平面平行（由教師用模型展示）（2）讓學生觀察書本的形狀，得出兩條對邊所在直線平

3、行。接著讓學生翻開書的封面觀察封面邊緣所在直線與書面所在平面的位置關系，通過觀察得出，它們平行。抽象出實驗中的兩條直線與一個平面，做出對應的圖形。將生活中的實物抽象成數學圖形.抽象：如何判定線面平行？復習回顧線面關系及線面平行的定義，為后面的學習做好鋪墊將生活中的實物抽象為幾何圖形，直觀感知線面位置關系.通過設置情境進一步讓學生體會線面位置關系普遍存在在我們的生活中；通過實際問題的提出，引發學生的認知沖突，激發學生的學習興趣，使判定定理的引入更加迫切與自然.讓學生完整體會數學概念和問題的抽象與提煉過程.探究說理操作確認【自主探究】探究：動手操作：設紙張的一邊AB所在直線為直線a，如圖，將紙張進

4、行翻折，設底面為，折痕CD所在直線為直線b問題1：怎樣翻折才能使得直線a與底面平行？問題2：當a/b時，轉動四邊形ABCD，轉動過程中，直線a與平面的位置關系是怎樣的？定理的發現采用“直觀感知實驗探究操作確認歸納提煉”的過程，讓學生清楚的看到線面平行的關鍵因素是什么，讓學生在自主探究和合作中，通過問題的引導思維逐步深入.教材并沒有要求證明判定定理，但考慮到歐式幾何的公理化體系，數學的嚴密性，這里采用說理的形式，讓學生深刻理解定理.歸納提煉得出定理問題3：根據以上分析，你覺得使直線a/的關鍵因素有哪些？（平面外一條線 平面內一條直線 這兩條直線平行）問題4：你能用三種語言描述我們得到的成果嗎？線

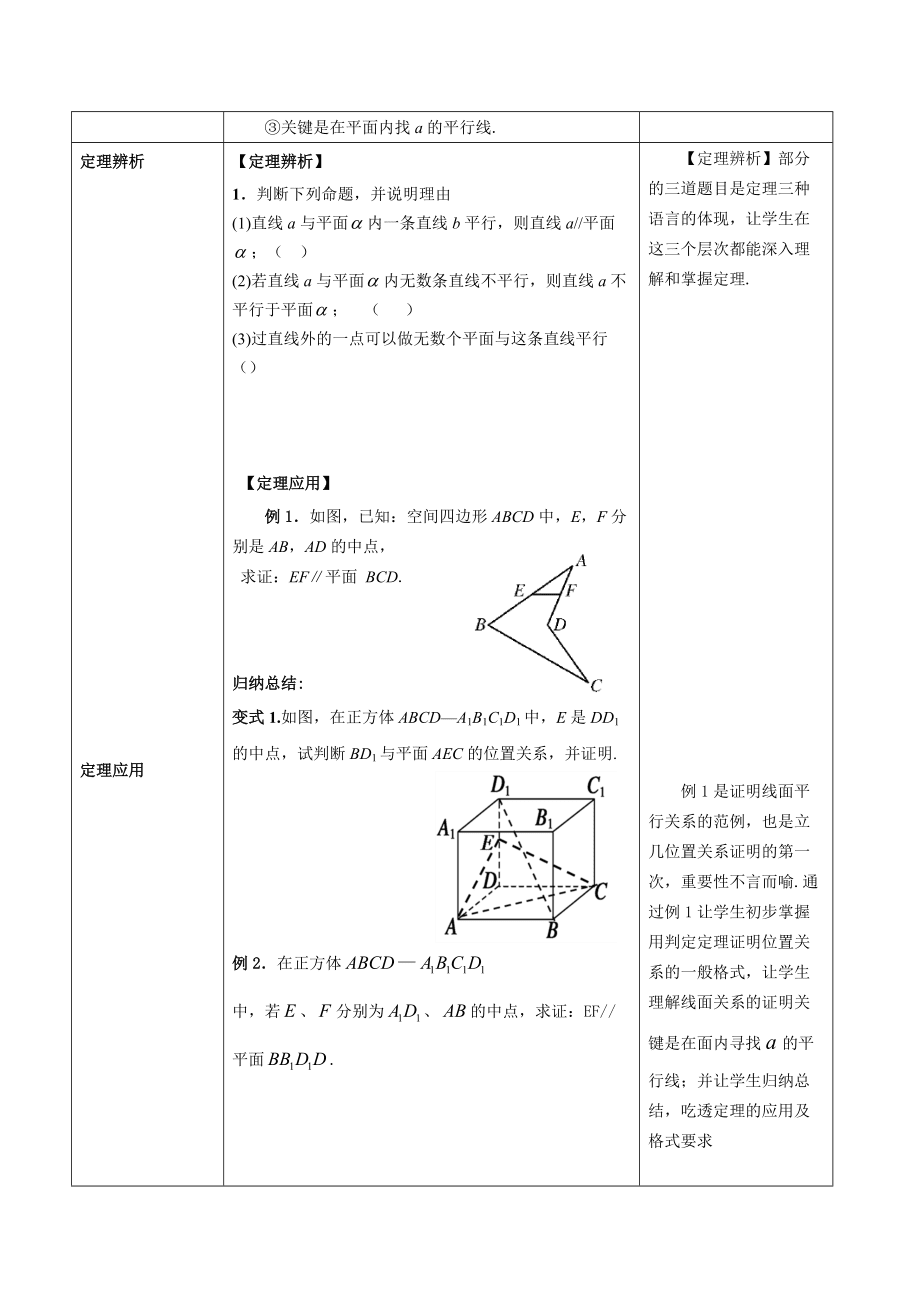
5、面平行的判定定理：平面外一條直線與此平面被一條直線平行，則該直線與此平面平行.符號語言：圖形語言：注：內外兩線平行，則線面平行； 線線平行線面平行（空間問題平面化）； 關鍵是在平面內找a的平行線.通過問題3，培養學生的抽象概括能力，逐步形成從探究活動中提煉數學原理與模型的能力.考慮到學生剛剛接觸線面位置關系，設計問題4，讓學生明白三種語言在立幾研究中的重要性，并為后面嚴密的數學推理與證明打下基礎.定理辨析定理應用【定理辨析】1判斷下列命題，并說明理由(1)直線a與平面內一條直線b平行，則直線a/平面；（ ）(2)若直線a與平面內無數條直線不平行，則直線a不平行于平面； （ ）(3)過直線外的一

6、點可以做無數個平面與這條直線平行（） 【定理應用】例1如圖，已知：空間四邊形ABCD中，E，F分別是AB，AD的中點，求證：EF平面 BCD.歸納總結:變式1.如圖，在正方體ABCDA1B1C1D1中，E是DD1的中點，試判斷BD1與平面AEC的位置關系，并證明.例2在正方體 中，若、分別為、的中點，求證：EF/平面.變式2. 如圖，四棱錐中，為線段上一點，為的中點證明：平面；【定理辨析】部分的三道題目是定理三種語言的體現，讓學生在這三個層次都能深入理解和掌握定理.例1是證明線面平行關系的范例，也是立幾位置關系證明的第一次，重要性不言而喻.通過例1讓學生初步掌握用判定定理證明位置關系的一般格式，讓學生理解線面關系的證明關鍵是在面內尋找a的平行線；并讓學生歸納總結，吃透定理的應用及格式要求例2主要強調平行四邊形及平行傳遞性在尋找平行直線時的應用；變式2是一道探究性題目，目的在于提高讓學生對輔助線的做法的認識.總結歸納總結提問：（1）這節課我們學習了哪些知識點以及方法？（2）在學習的過程中，我們應用了哪些數學思想？學生發言，互