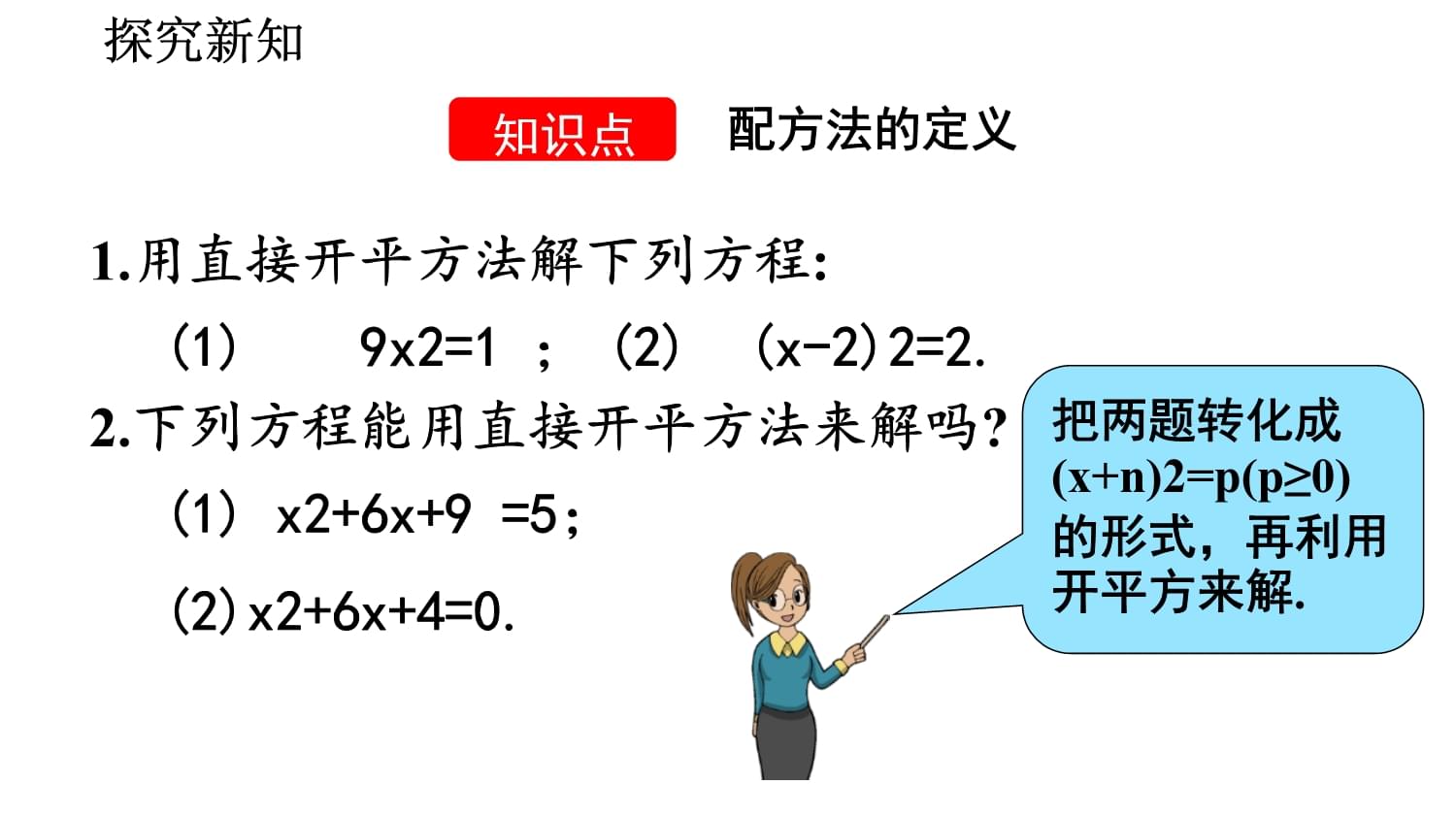
1、21.2 解一元二次方程21.2.1 配方法（第2課時(shí)）人教版 數(shù)學(xué) 九年級(jí) 上冊(cè)化為一般式，得 x2+6x-16=0 要使一塊矩形場(chǎng)地的長(zhǎng)比寬多6米，并且面積為16平方米，求場(chǎng)地的長(zhǎng)和寬應(yīng)各是多少？x(x+6)=16導(dǎo)入新知解：設(shè)場(chǎng)地寬為xm，則長(zhǎng)為（ x 6）m，根據(jù)長(zhǎng)方形面積為16m2，列方程得 怎樣解這個(gè)方程？能不能用直接開平方法？(1) 9x2=1 ；(2) (x-2)2=2.2.下列方程能用直接開平方法來解嗎?1.用直接開平方法解下列方程:(1) x2+6x+9 =5；(2)x2+6x+4=0.把兩題轉(zhuǎn)化成(x+n)2=p(p0)的形式，再利用開平方來解.探究新知配方法的定義知識(shí)點(diǎn)

2、 你還記得嗎？填一填下列完全平方公式.(1) a2+2ab+b2=( )2；(2) a2-2ab+b2=( )2.a+ba-b探究新知填一填（根據(jù) ）配方時(shí), 等式兩邊同時(shí)加上的是一次項(xiàng)系數(shù)一半的平方.56你發(fā)現(xiàn)了什么規(guī)律？二次項(xiàng)系數(shù)都為1.探究新知【思考】 怎樣解方程: x2+6x+4=0（1）（1）方程(1)怎樣變成（x+n)2=p的形式呢？解：x2+6x+4=0 x2+6x=-4移項(xiàng) x2+6x+9=-4+9兩邊都加上9二次項(xiàng)系數(shù)為1的完全平方式：常數(shù)項(xiàng)等于一次項(xiàng)系數(shù)一半的平方.探究新知（2）為什么在方程x2+6x=-4的兩邊加上9？加其他數(shù)行嗎？ 提示：不行，只有在方程兩邊加上一次項(xiàng)系

3、數(shù)一半的平方，方程左邊才能變成完成平方x2+2bx+b2的形式.探究新知 像上面那樣，通過配成完全平方形式來解一元二次方程的方法叫做配方法. 配方是為了降次 ，把一個(gè)一元二次方程轉(zhuǎn)化成兩個(gè)一元一次方程來解.配方法的定義探究新知例1 解方程：解：（1）移項(xiàng)，得x28x=1,配方，得x28x+42=1+42 ,( x4)2=15由此可得素養(yǎng)考點(diǎn) 1探究新知解二次項(xiàng)系數(shù)是1的一元二次方程解方程x2+8x-4=0解：移項(xiàng)，得 x2+8x4 配方，得 x2+8x+4=4+4， 整理，得 (x+4)2=20， 由此可得 x+4= ， x1 ， x2 .鞏固練習(xí)配方，得由此可得二次項(xiàng)系數(shù)化為1，得解：移項(xiàng)，

4、得2x23x=1,例2 解方程解二次項(xiàng)系數(shù)不是1的一元二次方程素養(yǎng)考點(diǎn) 2探究新知（1）移項(xiàng)和二次項(xiàng)系數(shù)化為1這兩個(gè)步驟能不能交換一下呢?配方，得 因?yàn)閷?shí)數(shù)的平方不會(huì)是負(fù)數(shù)，所以x取任何實(shí)數(shù)時(shí)，上式都不成立，所以原方程無實(shí)數(shù)根解：移項(xiàng)，得二次項(xiàng)系數(shù)化為1，得為什么方程兩邊都加12？即探究新知（2）思考1：用配方法解一元二次方程時(shí)，移項(xiàng)時(shí)要注意些什么？思考2：用配方法解一元二次方程的一般步驟.移項(xiàng)時(shí)需注意改變符號(hào).移項(xiàng)，二次項(xiàng)系數(shù)化為1；左邊配成完全平方式；左邊寫成完全平方形式；降次；解一次方程.探究新知一般地，如果一個(gè)一元二次方程通過配方轉(zhuǎn)化成 (x+n)2=p.當(dāng)p0時(shí),則 ,方程的兩個(gè)根為

5、當(dāng)p=0時(shí),則(x+n)2=0,x+n=0,開平方得方程的兩個(gè)根為 x1=x2=-n.當(dāng)p0時(shí),則方程(x+n)2=p無實(shí)數(shù)根. 方法點(diǎn)撥探究新知解下列方程：鞏固練習(xí)解: 移項(xiàng)，得配方，得由此可得二次項(xiàng)系數(shù)化為1，得整理，得3x2+6x=4x2+2x=x2+2x+12= +12(x+1)2=即 x+1= .x1= ， x2= .（1）鞏固練習(xí)解: 移項(xiàng)，得配方，得由此可得二次項(xiàng)系數(shù)化為1，得整理，得x1= ， x2= 4x2-6x=3x2- x=（2）鞏固練習(xí)解：移項(xiàng)，得 x取任何實(shí)數(shù)，上式都不成立，即原方程無實(shí)數(shù)根 對(duì)任何實(shí)數(shù)x都有 ( x+1 )2 0,配方，得 x2+2x+1=-2+1.

6、整理，得x2+2x=-2.(x+1)2=-1.（3）鞏固練習(xí)解：去括號(hào)，得 x2+4x=8x+12 移項(xiàng)，得 配方，得 由此可得 x-2=4整理，得x2-4x=12(x-2)2=16x1=6 , x2=-2x2-4x+2=12+2因此（4）例3 試用配方法說明：不論k取何實(shí)數(shù)，多項(xiàng)式 k24k5 的值必定大于零.解：k24k5=k24k41=（k2）21因?yàn)椋╧2）20，所以（k2）211.所以k24k5的值必定大于零.利用配方法確定多項(xiàng)式或字母的值（或取值范圍）素養(yǎng)考點(diǎn) 3探究新知方法點(diǎn)撥：證明代數(shù)式的值恒為正數(shù),需要利用配方法將代數(shù)式化成幾個(gè)非負(fù)數(shù)的和,利用非負(fù)數(shù)的性質(zhì)說明代數(shù)式的值恒為正

7、數(shù).例4 若a,b,c為ABC的三邊長(zhǎng)，且 試判斷ABC的形狀.解：對(duì)原式配方，得 根據(jù)非負(fù)數(shù)的性質(zhì)得 根據(jù)勾股定理的逆定理可知，ABC為直角三角形. 探究新知由此可得 即 鞏固練習(xí)方程2x2 - 3m - x +m2 +2=0有一個(gè)根為x = 0，則m的值為（ ） A. 1 B.1 C.1或2 D.1或-2應(yīng)用配方法求最大值或最小值.(1)求 2x2 - 4x+5的最小值 (2) -3x2 + 12x -16的最大值.C解：原式 = 2(x - 1)2 +3 因?yàn)?2(x - 1)2 0，所以 2(x - 1)2 +3 3因此當(dāng)x =1時(shí)，原式有最小值3.解：原式= -3(x - 2)2 -

8、 4 因?yàn)?(x - 2)2 0，即-3(x - 2)2 0，所以 -3(x - 2)2 -4-4因此當(dāng)x =2時(shí)，原式有最大值-4. 類 別解 題 策 略1.求最值或證明代數(shù)式的值恒為正（或負(fù)）對(duì)于一個(gè)關(guān)于x的二次多項(xiàng)式通過配方成a(x+m)2n的形式后，由于x無論取任何實(shí)數(shù)都有(x+m)20，n為常數(shù)，當(dāng)a0時(shí)，可知其有最小值；當(dāng)a0時(shí)，可知其有最大值.2.完全平方式中的配方如：已知x22mx16是一個(gè)完全平方式，所以一次項(xiàng)系數(shù)一半的平方等于16，即m2=16，m=4.3.利用配方構(gòu)成非負(fù)數(shù)和的形式對(duì)于含有多個(gè)未知數(shù)的二次式的等式，求未知數(shù)的值，解題突破口往往是通過配方成多個(gè)完全平方式得其

9、和為0，再根據(jù)非負(fù)數(shù)的和為0，各項(xiàng)均為0，從而求解.如：a2b24b4=0,則a2(b2)2=0,即a=0，b=2.配方法的應(yīng)用探究新知1. 一元二次方程y2y =0配方后可化為（） A. (y+ )2=1 B. (y- )2=1 C. (y+ )2= D. (y- )2=B連接中考課堂檢測(cè)1. 解方程：4x2-8x-4=0. 解：移項(xiàng)，得4x2-8x=4， 基礎(chǔ)鞏固題二次項(xiàng)系數(shù)化為1，得x2-2x=1， 配方，得 x2-2x+1=1+1,整理，得 （x-1）2=2,課堂檢測(cè)2.利用配方法證明：不論x取何值，代數(shù)式x2x1的值總是負(fù)數(shù)，并求出它的最大值.課堂檢測(cè)3.若 ，求(xy)z 的值.解：對(duì)原式配方，得 由非負(fù)數(shù)的性質(zhì)可知 4.如圖，在一塊長(zhǎng)35m、寬26m的矩形地面上，修建同樣寬的兩條互相垂直的道路，剩余部分栽種花草，要使剩余部分的面積為850m2，道路的寬應(yīng)為多少？解：設(shè)道路的寬為xm, 根據(jù)題意得（35-x)(26-x)=850，整理得x2-61x+60=0.解得x1=60（不合題意，舍去）, x2=1.答：道路的寬為1m.課堂檢測(cè)已知a,b,c為ABC的三邊長(zhǎng)，且 試判斷ABC的形狀.解：對(duì)原式配方，得 由代