1、第五章三角函數(shù)學(xué)案（1）角的推廣（一）目標(biāo)1.掌握用“旋轉(zhuǎn)”定義角的概念，理解并掌握“正角”負角”“象限角”“終邊相同的角”的含義；2.掌握所有與角終邊相同的角(包括角)的表示方法；3體會運動變化觀點，深刻理解推廣后的角的概念.復(fù)習(xí)1初中是如何定義角的？2初中我們所接觸的角的范圍是新課“（初中所學(xué)習(xí)的角的意義是否有些狹隘？（在體操比賽中我們經(jīng)常聽到這樣的術(shù)語：轉(zhuǎn)體720”（即轉(zhuǎn)體2周），轉(zhuǎn)體1080”即轉(zhuǎn)體3周）；如時鐘快了5分鐘，現(xiàn)要校正，需將分針怎樣旋轉(zhuǎn)？如果慢了5分鐘，又該如何校正？在奧運會上跳水運動員的跳水難度系數(shù)經(jīng)常有轉(zhuǎn)體多少多少度，這些度數(shù)是否超過了我們初中所學(xué)角的范圍？）1角的新

2、定義：（請試著標(biāo)出關(guān)鍵詞）2推廣后的角可以如何進行分類？3什么叫解析法？4象限角是如何定義的？5什么叫做終邊相同的角？6試著在0到2000范圍內(nèi)寫出與30的終邊相同的角.觀察有沒有什么規(guī)律，這樣的規(guī)律如何表示.結(jié)論：所有與終邊相同的角連同在內(nèi)可以構(gòu)成一個集合：7相等的角終邊一定相同，那終邊相同的角一定相等嗎？例1在0到360范圍內(nèi)，找出與下列各角終邊相同的角，并判斷它是哪個象限的角.(1)120(2)640(3)95012例2寫出與下列各角終邊相同的角的集合S，并把S中在360720間的角寫出來：（1）60（2）21（3）36314.練習(xí)1銳角是第幾象限的角？第一象限的角是否都是銳角？小于90

3、的角是銳角嗎？090的角是銳角嗎？2已知角的頂點與坐標(biāo)系原點重合，始邊落在x軸的正半軸上，作出下列各角，并指出它們是哪個象限的角？(1)420(2)75(3)855(4)510“注意:以后凡是沒有給出始邊落在x軸的正半軸上”都默認為此條件.作業(yè)1下列命題中正確的是()（A）終邊在y軸非負半軸上的角是直角（B）第二象限角一定是鈍角（C）第四象限角一定是負角（D）若360（Z），則與終邊相同2與120角終邊相同的角是()（A）600k360，Z（B）120k360，Z（C）120(2k1）180，Z（D）660k360，Z3若角與終邊相同，則一定有()（A）180（B）0（C）360，Z（D）36

4、0，Z4與1840終邊相同的最小正角為，與1840終邊相同的最小正角是.5今天是星期一，100天后的那一天是星期，100天前的那一天是星期.6鐘表經(jīng)過4小時，時針與分針各轉(zhuǎn)了(填度).7在直角坐標(biāo)系中，作出下列各角(1)360(2)720(3)1080(4)14408已知A銳角，B0到90的角，C第一象限角，D小于90的角求:AB，AC，CD，AD.9將下列各角表示為360（Z，0360）的形式，并判斷角在第幾象限（1）56024（2）56024（3）290315（4）290315（5）3900（6）390010寫出終邊落在第一象限角的角集合:寫出終邊落在第二象限角的角集合:寫出終邊落在第三象

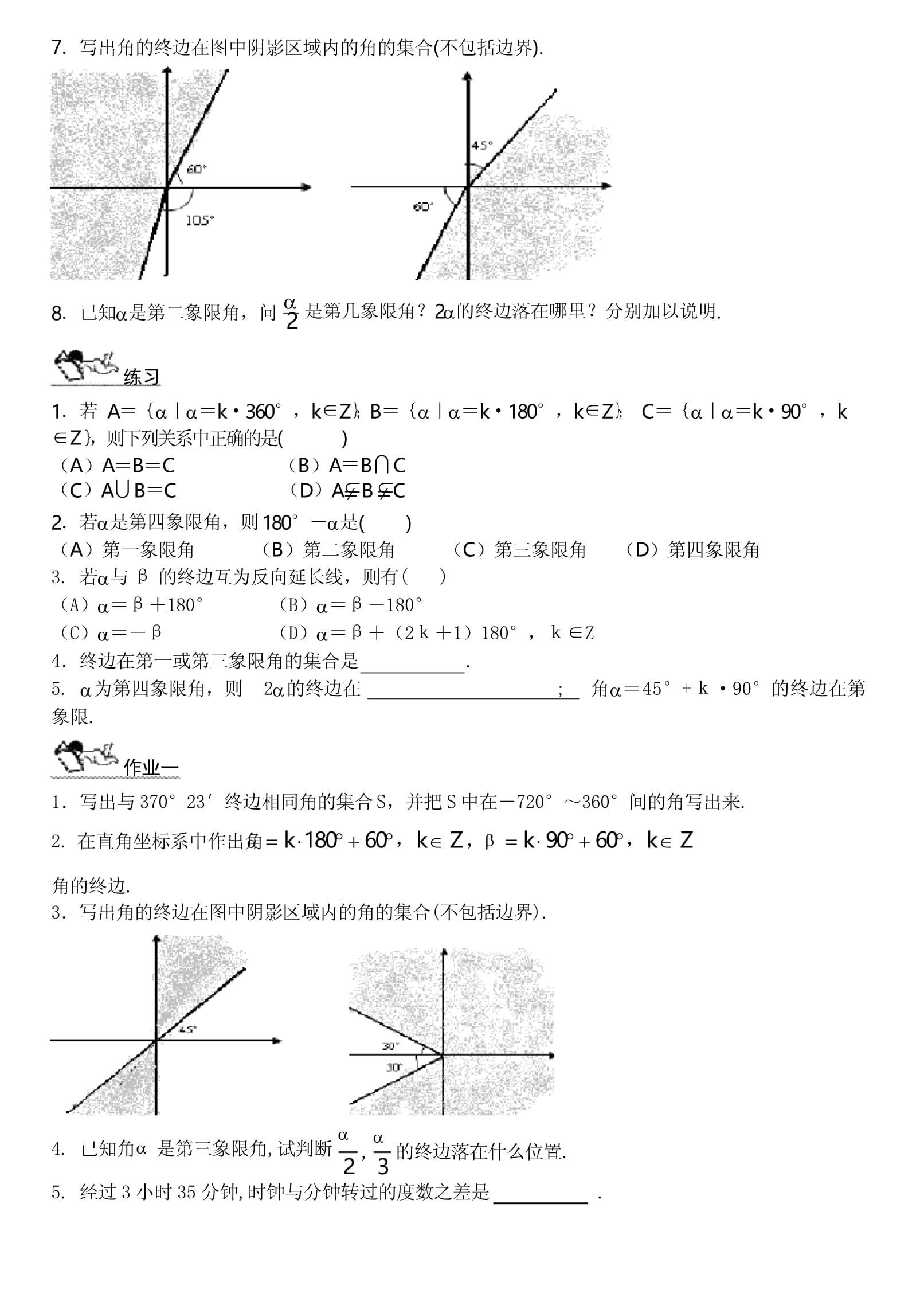
5、限角的角集合:寫出終邊落在第四象限角的角集合:11試寫出終邊落在x軸正半軸的所有角的集合:學(xué)案（2）角的推廣（二）目標(biāo)1鞏固角的形成，正角、負角、零角等概念，熟練掌握掌握所有與角終邊相同的角（包括角）、象限角、區(qū)間角、終邊在坐標(biāo)軸上的角的表示方法；2掌握所有與角終邊相同的角（包括角）、象限角、終邊在坐標(biāo)軸上的角的表示方法；3體會運動變化觀點，逐漸學(xué)會用動態(tài)觀點分析解決問題.復(fù)習(xí)1角的概念的推廣.2正角、負角、零角.3象限角、終邊相同的角.4寫出終邊在y軸上的角的集合.5寫出所有軸上角的集合.6用區(qū)間的形式表示象限角.7寫出角的終邊在圖中陰影區(qū)域內(nèi)的角的集合(不包括邊界).2是第幾象限角？2的終

6、邊落在哪里？分別加以說明.8已知是第二象限角，問（C）ABC（D）ABC練習(xí)1若Ak360，kZ；Bk180，kZ；Ck90，kZ，則下列關(guān)系中正確的是()（A）ABC（B）ABC2若是第四象限角，則180是()（A）第一象限角（B）第二象限角（C）第三象限角（D）第四象限角3.若與的終邊互為反向延長線，則有()（A）180（B）180（C）（D）（21）180，Z4終邊在第一或第三象限角的集合是.5.為第四象限角，則2的終邊在;角45+90的終邊在第象限.作業(yè)一1寫出與37023終邊相同角的集合S，并把S中在720360間的角寫出來.2.在直角坐標(biāo)系中作出角k18060，kZ，k9060，k

7、Z角的終邊.3寫出角的終邊在圖中陰影區(qū)域內(nèi)的角的集合(不包括邊界).4.已知角是第三象限角,試判斷,的終邊落在什么位置.235.經(jīng)過3小時35分鐘,時鐘與分鐘轉(zhuǎn)過的度數(shù)之差是.6.集合A|60k360,kZ,B|60k270,kZC|60k180,kZ那么集合A,B,C的關(guān)系如何?作業(yè)二1在|3601440中與2116終邊相同的角有()（A）1個（B）2個（C）3個（D）4個2.在|3601620中與2116終邊相同的角有()（A）2個（B）3個（C）4個（D）5個3.角45180，Z的終邊落在()（A）第一或第三象限（B）第一或第二象限（C）第二或第四象限（D）第三或第四象限4.第二象限角的

8、集合可表示為.5.角的終邊落在一、三象限角平分線上，則角的集合是.6.角是第二象限角，則180是第象限角；是第象限角；180是第_象限角.學(xué)案（3）弧度制目標(biāo)1理解弧度制的定義；2掌握角度與弧度的換算公式并能熟練地進行角度與弧度的換算；3熟記特殊角的弧度數(shù).復(fù)習(xí)1角的概念的推廣.2正角、負角、零角.3象限角、終邊相同的角.4寫出終邊在y軸上的角的集合.5.寫出所有軸上角的集合.6.用區(qū)間的形式表示象限角.新課1.什么是弧度制？2.弧度與角度如何進行轉(zhuǎn)換？3.試理解下圖正角零角負角正實數(shù)零負實數(shù)4.弧長公式與扇形面積公式：例1把6730化成弧度例2把3rad化成度5注意幾點：1度數(shù)與弧度數(shù)的換算

9、也可借助“計算器”進行；“2今后在具體運算時，弧度”二字和單位符號“rad”可以省略.如：3表示3rad，sin表示rad角的正弦；3一些特殊角的度數(shù)與弧度數(shù)的對應(yīng)值應(yīng)該記住：030456090120135150180270360弧度例3用弧度制表示：1.終邊在x軸上的角的集合2.終邊在y軸上的角的集合3.終邊在坐標(biāo)軸上的角的集合練習(xí)1.下列各對角中終邊相同的角是()（A）和222k（Z）（B）22和3371120122（C）和（D）和99392.若3，則角的終邊在()（A）第一象限（B）第二象限（C）第三象限（D）第四象限3.若是第四象限角，則一定在()（A）第一象限（B）第二象限（C）第三

10、象限（D）第四象限4.(用弧度制表示)第一象限角的集合為，第一或第三象限角的集合為.5.7弧度的角在第象限，與7弧度角終邊相同的最小正角為.6.圓弧長度等于其圓的內(nèi)接正三角形邊長，則其圓心角的弧度數(shù)為.3tan7.(選做)求值：sin3tan6cos6tan4cos2.8.已知集合A22，Z，B44，求AB.9.現(xiàn)在時針和分針都指向12點，試用弧度制表示15分鐘后，時針和分針的夾角.作業(yè)已知是第二象限角，試說明下列各角終邊所在位置：(1)(2)(3)223學(xué)案（4）三角函數(shù)的定義目標(biāo)1.理解并掌握任意角三角函數(shù)的定義；2.理解三角函數(shù)是以實數(shù)為自變量的函數(shù)；3.掌握正弦、余弦、正切函數(shù)的定義域

11、.新課在初中，我們對于三角函數(shù)的定義是基于直角三角形，而到了高中階段，我們要在直角坐標(biāo)系的圓里進行定義.1.設(shè)是一個任意角，在的終邊上任取（異于原點的）一點P（x,y）則P與原點的距離rx2y2x2y20.2比值yr叫做的正弦記作：sinyrxx比值叫做的余弦記作：cosrry比值叫做的正切記作：tanxyx比值xy叫做的余切記作：cotxy比值rr叫做的正割記作：secxx比值ry叫做的余割記作：cscry2(kZ)時，終邊上任意一點P根據(jù)相似三角形的知識，對于終邊不在坐標(biāo)軸上確定的角，上述六個比值都不會隨P點在的終邊上的位置的改變而改變.當(dāng)角的終邊在縱軸上時，即k的橫坐標(biāo)x都為0，所以ta

12、n、sec無意義；當(dāng)角的終邊在橫軸上時，即（Z）時，終邊上任意一點P的縱坐標(biāo)都為0，所以cot、csc無意義，除此之外，對于確定的角，上面的六個比值都是惟一確定的實數(shù)，這就是說，正弦、余弦、正切、余切、正割、余割都是以角為自變量，以比值為函數(shù)值的函數(shù).以上六種函數(shù)，統(tǒng)稱為三角函數(shù).3.探究:角是“任意角”，當(dāng)=2k(kZ)時，與的同名三角函數(shù)值應(yīng)該是相等的，即凡是終邊相同的角的三角函數(shù)值相等.實際上，如果終邊在坐標(biāo)軸上，上述定義同樣適用.三角函數(shù)是以“比值”為函數(shù)值的函數(shù).r0而x,y的正負是隨象限的變化而不同，故三角函數(shù)的符號應(yīng)由象限確定.定義域：對于正弦函數(shù)sinyy，因為0，所以恒rr有

13、意義，即取任意實數(shù)，yr恒有意義，也就是說sin恒有意義，所以正弦函數(shù)的定義域是R；類似地可寫出余弦函數(shù)的定義，因為x0時，域；對于正切函數(shù)tanyy無意義，即tanxx無意義，又當(dāng)且僅當(dāng)角的終邊落在縱軸上時，才有x0，所以當(dāng)?shù)慕K邊不在縱軸上時，yx恒有意義，即tan恒有意義，所以正切函數(shù)的定義域是k2(kZ).從而有：k(kZ)ysinRycotRycosyseck(kZ)2ycscytank(kZ)k(kZ)24.注意:(1)以后我們在平面直角坐標(biāo)系內(nèi)研究角的問題，其頂點都在原點，始邊都與x軸的非負半軸重合.(2)OP是角的終邊，至于是轉(zhuǎn)了幾圈，按什么方向旋轉(zhuǎn)的不清楚，也只有這樣，才能說明

14、角是任意的.(3)定義中只說怎樣的比值叫做的什么函數(shù)，并沒有說的終邊在什么位置(終邊在坐標(biāo)軸上的除外)，即函數(shù)的定義與的終邊位置無關(guān).(4)比值只與角的大小有關(guān).例1已知角的終邊經(jīng)過點P(2，3)(如圖)，求的六個三角函數(shù)值.例2填表：030456090120135150180270360弧度sincostancotseccsc例3（1）已知角的終邊經(jīng)過P(4,3),求2sincos的值（2）已知角的終邊經(jīng)過P(4a,3a),(a0)求2sincos的值例4求函數(shù)y練習(xí)cosxtanxcosxtanx的值域1.若點P(3，)是角終邊上一點，且sin23，則的值是.2.角的終邊上一個點P的坐標(biāo)為

15、(5a,12a)(a0)，求sin2cos的值.3.已知sin2cos，求sin4cos5sin2cos及sin22sincos的值.sin04試理解角為第三象限角的充分必要條件是tan05已知tan=3，求下列各式的值.(1)4sincos3sin5cos(2)sin22sincoscos24cos23sin231(3)sin2cos242(5)sincos11(7)sincos(4)sincos(6)sincos(8)sin6cos66若4sin2cos5cos3sin10，則tan的值為.學(xué)案（5）同角三角函數(shù)的基本關(guān)系（一）目標(biāo)1掌握同角三角函數(shù)的基本關(guān)系式，理解同角公式都是恒等式的特

16、定意義；2通過運用公式的訓(xùn)練過程，培養(yǎng)解決三角函數(shù)求值、化簡、恒等式證明的解題技能，提高運用公式的靈活性；3.注意運用數(shù)形結(jié)合的思想解決有關(guān)求值問題；在解決三角函數(shù)化簡問題過程中，培養(yǎng)思維的靈活性及思維的深化；在恒等式證明的學(xué)習(xí)過程中，培養(yǎng)分析問題的能力，從而提高邏輯推理能力.復(fù)習(xí)1.三角函數(shù)的概念.2.三角函數(shù)值的符號.新課例1已知sin45，并且是第二象限角，求的其他三角函數(shù)值.例2已知cos練習(xí)817，求sin、tan的值.1已知cos12，求tan的值.2.已知sincos12，求下列各式的值.sin3cos3sin4cos4sin6cos613.已知sincos，且，則cossin的

17、值是多少.842學(xué)案（6）同角三角函數(shù)的基本關(guān)系（二）目標(biāo)1掌握同角三角函數(shù)的基本關(guān)系式，理解同角公式都是恒等式的特定意義；2通過運用公式的訓(xùn)練過程，培養(yǎng)解決三角函數(shù)求值、化簡、恒等式證明的解題技能，提高運用公式的靈活性；3注意運用數(shù)形結(jié)合的思想解決有關(guān)求值問題；在解決三角函數(shù)化簡問題過程中，培養(yǎng)思維的靈活性及思維的深化；在恒等式證明的學(xué)習(xí)過程中，培養(yǎng)分析問題的能力，從而提高邏輯推理能力.復(fù)習(xí)同角三角函數(shù)的基本關(guān)系公式：sin2cos21sincostancotcossintancot1cscsin1seccos1sin2cos21sec2tan21csc2cot211“同角”的概念與角的表達

18、形式無關(guān)，如：2sin2tansin23cos231cos22上述關(guān)系（公式）都必須在定義域允許的范圍內(nèi)成立.3一個角的任一三角函數(shù)值可求出這個角的其余各三角函數(shù)值，且因為利用“平方關(guān)系”公式，最終需求平方根，會出現(xiàn)兩解，因此應(yīng)盡可能少用,若使用時,要注意討論符號.sincos這些關(guān)系式還可以如圖樣加強形象記憶：對角線上兩個函數(shù)的乘積為1(倒數(shù)關(guān)系).任一角的函數(shù)等于與其相鄰的兩個函數(shù)的積(商數(shù)關(guān)系).陰影部分，頂角兩個函數(shù)的平方和等于底角函數(shù)的平方(平方關(guān)系).新課例1化簡：1sin2440.tan1cotseccsc例2已知是第三象限角，化簡1sin1sin.1sin1sin例3求證：co

19、s1sin.1sincos求sin的值.，例4已知方程2x2(31)xm0的兩根分別是sincos，cos1cot1tanxsincos例5（選講）消去式子中的：ytancot例6已知sin2sin,tan3tan,求cos2.練習(xí)1已知cot=2，求的其余三個三角函數(shù)值.2已知：sin15且tan0，試用定義求的其余三個三角函數(shù)值.（1）1cos3已知角的終邊在直線y=3x上，求sin和cos的值.4化簡下列各式，其中(,)21cos1cos1cos（2）sintansin1costansin（3）sin1sin21cos2cos5求證：(2cos2)(12cot2)(2cot2)(2sin

20、2).6已知asecctand,bsecdtanc.求證：a2b2c2d2作業(yè)（A）31.已知sincos13，且0，則tan的值為(23（B）3（C）（D）3332.若sin4cos41，則sincos的值為()（A）0（B）1（C）1（D）13.若tancot2，則sincos的值為()（A）0（B）2（C）2（D）24.若tancot=2，則sin4cos4.5.若tan2cot22，則sincos.)6.求證1sin6xcos6x3.1sin4xcos4x27已知tancot2，求sin3cos3的值.學(xué)案(7)誘導(dǎo)公式（一）目標(biāo)1理解并掌握各種三角函數(shù)在各象限內(nèi)的符號；2理解并掌握誘

21、導(dǎo)公式.復(fù)習(xí)1寫出下面函數(shù)的定義域ysinycotycosysecytanycsc2上述函數(shù)值的正負是什么樣的.3終邊相同的角的三角函數(shù)值有什么樣的關(guān)系.4終邊關(guān)于x軸對稱的角的三角函數(shù)值有什么樣的關(guān)系.5終邊關(guān)于y軸對稱的角的三角函數(shù)值有什么樣的關(guān)系.6終邊關(guān)于原點對稱的角的三角函數(shù)值有什么樣的關(guān)系.例1確定下列三角函數(shù)值的符號.4)(1)cos250（2）sin(例2求下列三角函數(shù)的值.（3）tan（672）(4)tan113(1)cos911(2)tan()46例3求值：sin(1320)cos1110+cos(1020)sin750+tan4950練習(xí)1確定下列各式的符號(1)sin1

22、00cos240(2)sin5tan52x取什么值時,sinxcosxtanx有意義?5已知是第三象限角且cos0，問是第幾象限角？3若三角形的兩內(nèi)角，滿足sincos0)的最大值為2,最小值為4，求k,b的值.5求下列函數(shù)的定義域：(1)y=3cosx12cos2x(2)y=lg(2sinx1)2cosx1學(xué)案（19）三角函數(shù)的圖象與性質(zhì)（二）目標(biāo)1理解正、余弦函數(shù)的定義域、值域、最值、周期性、奇偶性的意義；2會求簡單函數(shù)的定義域、值域、最小正周期和單調(diào)區(qū)間；3掌握正弦函數(shù)yAsin(x)的周期及求法.復(fù)習(xí)1y=sinx，xR和y=cosx，xR的圖象.：2用五點法作正弦函數(shù)和余弦函數(shù)的簡圖

23、（描點法）正弦函數(shù)y=sinx，x0，2的圖象中，五個關(guān)鍵點是：(0,0)(23,1)(,0)(,1)(2,0)2余弦函數(shù)y=cosxx0,2的五個點關(guān)鍵是(0,1)(23,0)(,1)(,0)(2,1)23定義域：正弦函數(shù)、余弦函數(shù)的定義域都是實數(shù)集R.分別記作：ysinx，xRycosx，xR4值域正弦函數(shù)、余弦函數(shù)的值域都是1，1,其中正弦函數(shù)y=sinx,xR當(dāng)且僅當(dāng)x22k，kZ時，取得最大值1.當(dāng)且僅當(dāng)x2k，kZ時，取得最小值1.2而余弦函數(shù)ycosx，xR當(dāng)且僅當(dāng)x2k，kZ時，取得最大值1.當(dāng)且僅當(dāng)x(2k1)，kZ時，取得最小值1.5周期性一般地，對于函數(shù)f(x)，如果存在

24、一個非零常數(shù)T，使得當(dāng)x取定義域內(nèi)的每一個值時，都有f(xT)f(x)，那么函數(shù)f(x)就叫做周期函數(shù)，非零常數(shù)T叫做這個函數(shù)的周期.對于一個周期函數(shù)f(x)，如果在它所有的周期中存在一個最小的正數(shù)，那么這個最小正數(shù)就叫做f(x)的最小正周期.1）周期函數(shù)x屬于定義域M，則必有xTM,且若T0則定義域無上界；T0且A1)的圖象可以看作把正數(shù)曲線上的所有點的縱坐標(biāo)伸長(A1)或縮短(0A1)到原來的A倍得到的它的值域A,A最大值是A,最小值是A若A0且1)的圖象，可看作把正弦曲線上所有點的橫坐標(biāo)縮短(1)或伸長(01)到原來的1倍（縱坐標(biāo)不變）若0則可用誘導(dǎo)公式將符號“提出”再作圖決定了函數(shù)的周

25、期.x3相位變換:函數(shù)ysin(x)，R(其中0)的圖象，可以看作把正弦曲線上所有點向左(當(dāng)0時)或向右(當(dāng)0時)平行移動個單位長度而得到(用平移法注意：“左加”“右減”).新課例1畫出函數(shù)y3sin(2x3)，xR的簡圖，觀察與y=sinx圖象有什么樣的關(guān)系.例2已知如圖是函數(shù)y2sin(x)其中的圖象，那么()21010（A），（B），111166（C）2，（D）2，66例3已知函數(shù)yAsin(x)，在同一周期內(nèi)，當(dāng)x函數(shù)取得最小值2，則該函數(shù)的解析式為()94時函數(shù)取得最大值2，當(dāng)x時9（A）y2sin(3x)（B）y2sin(3x)66xx（C）y2sin()（D）y2sin()363

26、6練習(xí)1已知函數(shù)yAsin(x)(A0，0，02)圖象的一個最高點(2，3)，由這個最高點到相鄰最低點的圖象與x軸交于點(6，0)，試求函數(shù)的解析式.2已知函數(shù)yAsin(x)(其中A0，2）在同一周期內(nèi)，當(dāng)x時，y有最12小值2，當(dāng)x712時，y有最大值2，求函數(shù)的解析式.3已知函數(shù)yAsin(x)在一個周期內(nèi)，當(dāng)x7時，取得最大值2，當(dāng)x時取得最1212小值2，那么()1(A)ysin(x)(B)y2sin(2x)233x(C)y2sin(2x)(D)y2sin()6264如圖，已知函數(shù)yAsin（x）的部分圖象，則函數(shù)的表達式為()（A）y2sin（10 x）（B）y2sin（11610 x）116（C）y2sin（2x）（D）y2sin（2x)6615函數(shù)y2sin（x）在一個周期內(nèi)的三個“零點”橫坐標(biāo)是()23511(A),(B)3332410,333112325(C),(D),6663336函數(shù)ysin（x2）（0）的周期為2，則7若函數(shù)yasinxb（a0)的最小值為13，最大值為，則a、b的值分別為_.228函數(shù)y3sin（2x）(0)為偶函數(shù)，則.附：作y=sinx（長度為2的某閉區(qū)間）沿x軸平移|個單位得y=sin(x+)橫坐標(biāo)伸長或縮短得y=sin(x+)縱坐標(biāo)伸長或縮短橫坐標(biāo)伸長或縮短