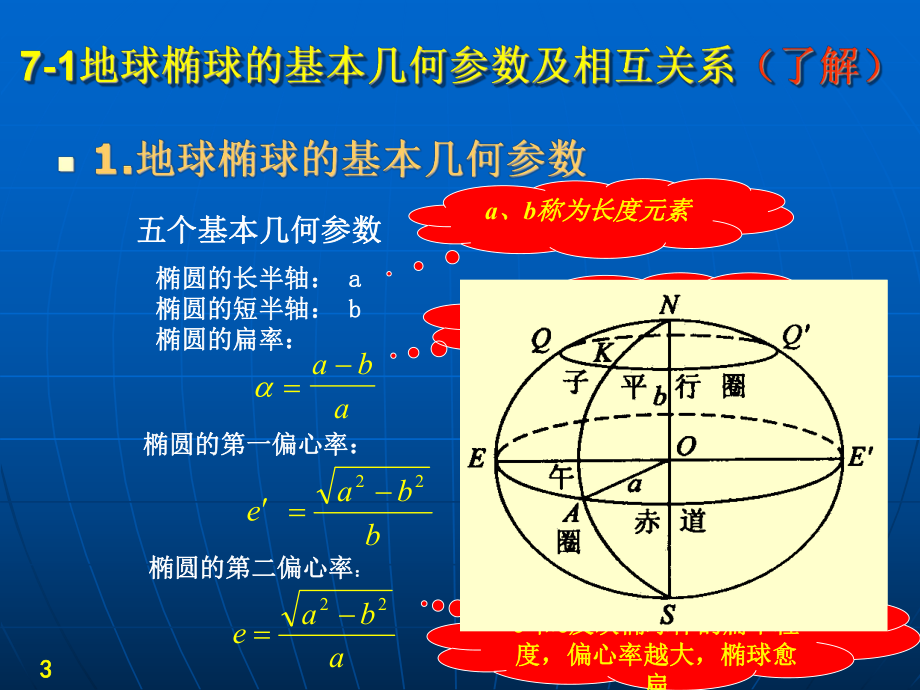
1、12 21地球橢球的定義及其幾何意義； 2常用測量坐標系統的建立及其在控制測量中的應用； 3各種測量坐標系統之間的相互轉換； 4橢球面上幾種曲率、弧長、大地線的計算； 5地面測量值（水平方向和邊長）歸算到橢球面的方法。知識點及學習要求知識點及學習要求難點在對本章的學習中，有大量的公式推導與應用。各種常用測量坐標系統的建立與相互轉換；幾種常用的橢球計算公式；地面觀測值歸算到橢球面的方法與計算。 3 3橢圓的長半軸：橢圓的長半軸： a a橢圓的短半軸：橢圓的短半軸： b b橢圓的扁率：橢圓的扁率： 五個基本幾何參數五個基本幾何參數 aba橢圓的第一偏心率：橢圓的第一偏心率： abae22橢圓的第二

2、偏心率橢圓的第二偏心率： bbae22 a、b稱為長度元素稱為長度元素扁率反映了橢球體的扁率反映了橢球體的扁平程度扁平程度 e和和e反映橢球體的扁平程反映橢球體的扁平程度，偏心率越大，橢球愈度，偏心率越大，橢球愈扁扁 4 42222,tan,cosactBeBb 22221sin,1cosWeB VeB 式中，式中，W W 第一基本緯度函數，第一基本緯度函數，V V 第二基本緯度函數。第二基本緯度函數。5 5 我國所采用的的我國所采用的的19541954年北京坐標系應用的是克年北京坐標系應用的是克拉索夫斯基橢球參數；以后采用的拉索夫斯基橢球參數；以后采用的19801980國家大地坐國家大地坐標

3、系應用的是標系應用的是19751975國際橢球參數；而國際橢球參數；而GPSGPS應用的是應用的是WGS-84WGS-84系橢球參數。系橢球參數。 6 62.地球橢球參數間的相互關系地球橢球參數間的相互關系abae22bbae22 eaba2222eabb22221222eba2221aeb ()( )11122eeeee2221eee22217 7abebae1122 caeace1122 eeeeee1122221 1eVWeWV8 8大地坐標系、大地坐標系、空間直角坐標系空間直角坐標系（大地測量中兩種基本坐標系）（大地測量中兩種基本坐標系）子午平面直角坐標系子午平面直角坐標系大地極坐標系

4、大地極坐標系 9 9 P點的子午面點的子午面NPS與起始子與起始子午面午面NGS所構成的二面角所構成的二面角叫做叫做P點點大地經度大地經度，P點的點的法線法線Pn與赤道面的夾角與赤道面的夾角B叫叫P點的點的大地緯度大地緯度，P點的位點的位置用置用L、B表示表示 。P)()(大地水準面差距高程異常正正常NHHHH若若P點不在橢球面上，還要點不在橢球面上，還要一個參數：一個參數：大地高大地高H來表示來表示點位。它與正常高及正高的點位。它與正常高及正高的關系為：關系為：1010以橢球中心以橢球中心O為原點，起為原點，起始子午面與赤道面交線始子午面與赤道面交線為為X軸，在赤道面上與軸，在赤道面上與X軸

5、正交的方向為軸正交的方向為Y軸，橢軸，橢球體的旋轉軸為球體的旋轉軸為Z軸，構軸，構成右手坐標系成右手坐標系O-XYZ，在該坐標系中，在該坐標系中，P點的位點的位置用置用X、Y、Z表示表示 1111設設P點的大地經度為點的大地經度為L，在過在過P點的子午面上，點的子午面上，以子午圈橢圓中心為以子午圈橢圓中心為原點，建立原點，建立x，y平面平面直角坐標系。在該坐直角坐標系。在該坐標系中，標系中，P點的位置點的位置用用L，x，y表示表示 1212 M為橢圓體面上任意為橢圓體面上任意一點，一點，MN為過為過M點的子點的子午線，午線，S為連結為連結MP的大的大地線長，地線長，A為大地線在為大地線在M點的

6、大地方位角。以點的大地方位角。以M為極點、為極點、MN為極軸、為極軸、S為極徑、為極徑、A為極角，就構為極角，就構成了大地極坐標系。成了大地極坐標系。P點點位置用位置用S、A表示。表示。 橢球面上的極坐標（橢球面上的極坐標（S、A）與大地坐標（）與大地坐標（L、B）可以互相換算，這種換算叫大地主題解算。可以互相換算，這種換算叫大地主題解算。1313xaBeBaBWcossincos1222222(1)sinsin(1)sin1sinaeBabByeBWVeB 過過p p 點作法線點作法線PnPn，它，它與與x 軸之夾角為軸之夾角為B，過點作，過點作子午圈的切線子午圈的切線TP，它與，它與x 軸

7、的夾角為（軸的夾角為（9090+ +B）- -該角的正切值為曲線在該角的正切值為曲線在P P點處切線的斜率點處切線的斜率. .1414設設Pn=N，則有：，則有：yP sinB2(1)PNe2nNecosxNBcosaBxWaNW2(1)sinayeBW2(1)sinyNeB一個有用的結論推導：一個有用的結論推導：1515cos,sin,XxL YxL Zy1616X XY Y2coscoscossin(1)sinXNBLYNBLZNeBcosxNB2(1)sinyNeBcos ,sin ,XxL YxL Zy當當P P點位于橢球面上時：點位于橢球面上時：1717BHeNLBHNLBHNZYX

8、sin)1 (sincos)(coscos)(2La rc tgYXZBNeYXctgBYXBNeZtgBcossin222222或NBYXHeNBZHcos)1(sin222當當P P點不在橢球面上時：點不在橢球面上時：18181919MaeW()123221sinWeBMaeceaeMcMaec022329021111()( )()2acb2020dBdSM BdxBDEdSsinsinMdxdBB 1sin2cossinWdBdWBBWadBdxdWdBdeBdBeBBeBeBBW122 1222222sinsincossinsincosdxdBaBWeBWaBWWeB sincossi

9、n(cos)12233222cosaBxWdxdBaBWeBeB sin(sincos)322221WeB2221sindxdBaBWe sin()321221sinWeBMaeW()123MdxdBB 1sin21212、卯酉圈曲率半徑、卯酉圈曲率半徑 NaW221sinWeBaN 02222平行圈平面與卯平行圈平面與卯酉圈平面之間的夾角即為大地緯酉圈平面之間的夾角即為大地緯度度B B，所以有：，所以有：rNBcos平行圈半徑平行圈半徑r就等于就等于P點的橫坐標點的橫坐標x（子午（子午面直角坐標系），即：面直角坐標系），即：xraBWcosNaW23233 3、任意法截弧的曲率半徑、任意法截

10、弧的曲率半徑22221(1)(1cos)2coscos22ARRARReBAR222coseB 當當A=0或或180時，時，RA的值最小，此時的值最小，此時R0=M（子午曲率（子午曲率半徑）當半徑）當A=90或或270時，時，RA的值最大，此時的值最大，此時R90=N（卯酉圈曲率半徑）；當（卯酉圈曲率半徑）；當A由由090時，時，RA之值由之值由MN；當當A由由90180時，時，RA之值由之值由NM。RA值的變化是以值的變化是以90為周期且與子午圈和卯酉圈對稱的。為周期且與子午圈和卯酉圈對稱的。24244 4、平均曲率半徑、平均曲率半徑M、N、R的關系：的關系：NR M只有在極點上，它們才相等

11、，且均等于極曲率半只有在極點上，它們才相等，且均等于極曲率半徑徑c，即：，即： 2222(1).bcNaRMNeWVVWNRMc909090 由于由于R RA A的數值隨方位的數值隨方位A A的變化而變化，給測量帶來不便，在測量工作中，的變化而變化，給測量帶來不便，在測量工作中，往往根據一定的精度要求，在一定范圍內，把橢球面當作球面來處理，為此，往往根據一定的精度要求，在一定范圍內，把橢球面當作球面來處理，為此，就要推求該球面的曲率半徑就要推求該球面的曲率半徑-平均曲率半徑平均曲率半徑 就是過橢球面上一點的一切法截就是過橢球面上一點的一切法截弧弧(0(022），當其數目趨于無窮時，它們的曲率半

12、徑的算術平均值的極限，），當其數目趨于無窮時，它們的曲率半徑的算術平均值的極限，就稱為平均曲率半徑，用就稱為平均曲率半徑，用R R表示表示 。25257.4 橢球面上的弧長計算橢球面上的弧長計算1.1.子午線弧長計算公式子午線弧長計算公式dxMdBBeBeBe44222322sin815sin231)sin1 (sincossincoscos241212238122184BBBBB32222244433(1sin)1 (cos2 )44451515(cos2cos4 )641664eBeeBeeBeB 2300(1)BBaeXMdBdBW221sinWeB將積分因子按二項式定理展開為級數形式將

13、積分因子按二項式定理展開為級數形式將正弦的指數函數化為余弦的倍數函數將正弦的指數函數化為余弦的倍數函數 322220(1)(1sin)BaeeBdB2626BCBBBAeaX4sin42sin2)1 (232222444233451515(1sin)1 (cos2 )(cos2cos4 )44641664eBeeBeeBeB Aee134456424B42161543eeC46415eXaeABBCBdBB() (coscos)1242027272.平行圈弧長公式平行圈弧長公式 cos llSrNB 旋轉橢球體的平行圈是一個圓，其半徑就是圓上任意一點的旋轉橢球體的平行圈是一個圓，其半徑就是圓上

14、任意一點的子午面直角坐標子午面直角坐標x：22coscos1sinaBrxNBeB如果平行圈上有兩點，其經如果平行圈上有兩點，其經差差 ，可寫出平行圈弧長公式：可寫出平行圈弧長公式： 12 LLl 28283.子午線弧長和平行圈弧長變化的比較子午線弧長和平行圈弧長變化的比較B 1 單位緯差的子午線弧長隨單位緯差的子午線弧長隨B B的增大而緩慢地增大；而單位的增大而緩慢地增大；而單位經差的平行圈弧長則隨經差的平行圈弧長則隨B B的增大而急劇縮短。同時還知，子午的增大而急劇縮短。同時還知，子午弧長弧長1 1約為約為110KM110KM，11約為約為1.8KM1.8KM，11約為約為30M30M；而

15、平行圈；而平行圈弧長僅在赤道附近才與子午線弧長大體相當，隨著弧長僅在赤道附近才與子午線弧長大體相當，隨著B B的增大它的增大它們的差值愈來愈大。們的差值愈來愈大。29297.5 大地線大地線 1.相對法截線的概念相對法截線的概念 （1）緯度不同的兩點，法線必）緯度不同的兩點，法線必交于旋轉軸的不同點；交于旋轉軸的不同點；（2）橢球面上一點的緯度愈高，）橢球面上一點的緯度愈高，法線與旋轉軸的交點愈低；法線與旋轉軸的交點愈低；（3）當兩點的緯度不同，又不）當兩點的緯度不同，又不在同一子午圈上時，這兩點的法在同一子午圈上時，這兩點的法線將在空間交錯而不相交。因此線將在空間交錯而不相交。因此當兩點不在

16、同一子午圈上，也不當兩點不在同一子午圈上，也不在同一平行圈上時，兩點間就有在同一平行圈上時，兩點間就有二條法截線存在。二條法截線存在。首先明確以下三點：首先明確以下三點：3030ABnb假定經緯儀的縱軸同假定經緯儀的縱軸同A，B兩點的兩點的法線重合（忽略垂線偏差），如法線重合（忽略垂線偏差），如此以兩點為測站，則經緯儀的照此以兩點為測站，則經緯儀的照準面就是準面就是法截面法截面。用用A點照準點照準B點，點，則照準面則照準面 同橢球面的截線同橢球面的截線為為 ，叫做，叫做A點的點的正法截線正法截線，或或B點的點的反法截線反法截線；同理，由；同理，由B照照A點，則照準面點，則照準面 同橢球面的同橢

17、球面的截線為截線為BbA ，叫做，叫做B點的點的正法截線正法截線，或或A點的點的反法截線反法截線。因。因A，B的法的法線互不相交，故這兩條法截線不線互不相交，故這兩條法截線不重合。我們把重合。我們把 和和BbA叫做叫做A、B兩點的兩點的相對法截線。相對法截線。 BAnaAaBAaB3131當當A A、B B兩點位于同一子午圈或同兩點位于同一子午圈或同一平行圈上時，正反法截線則合一平行圈上時，正反法截線則合二為一，這是一種特殊情況。而二為一，這是一種特殊情況。而通常情況下，正反法截線是不重通常情況下，正反法截線是不重合的。因此在橢球面上合的。因此在橢球面上A A、B B、C C三點處所測得的角度

18、三點處所測得的角度（各點上正（各點上正法截線之夾角）法截線之夾角）將不能構成閉合將不能構成閉合三角形。為克服這個矛盾，在兩三角形。為克服這個矛盾，在兩點間另選一條單一的點間另選一條單一的大地線大地線代代替相對法截線，從而得到由大地替相對法截線，從而得到由大地線構成的單一的三角形。線構成的單一的三角形。32322、大地線的定義和性質、大地線的定義和性質 橢球面上兩點間的最短曲線橢球面上兩點間的最短曲線叫做叫做大地線大地線。大地線是橢球面上兩點間唯一最短線，大地線是橢球面上兩點間唯一最短線，而且位于相對法截線之間，并靠近正而且位于相對法截線之間，并靠近正法截線，它與法截線，它與正正法截線間的夾角為

19、：法截線間的夾角為： 13在一等三角測量中，在一等三角測量中，可達千分之四秒，可達千分之四秒，可達千分之一二秒可達千分之一二秒 33333、大地線的微分方程和克萊洛、大地線的微分方程和克萊洛(克萊勞克萊勞)方程方程 dBAMdScosdSBNAdlcossin1）大地線微分方程）大地線微分方程: 表達表達dL，dB，dA與與dS的關系式。的關系式。MdBdSAcosAdSBdlNsincosdA PTr dl cossinsinrdlNBdlAdABdltgBdSPTNctgBNPTNctgB3434dBAMdScossin AdAtgBdSNBNBdBMAAdAcossincossincos

20、sinrNBMBdBdr rdrctgAdAlnsinlnlnArCrACsin代入代入兩邊積分得：兩邊積分得：麥尼兒定理：麥尼兒定理：3535rACsin1221sinsinAArr上式表明：在旋轉橢球面上，大地線各點的平行圈上式表明：在旋轉橢球面上，大地線各點的平行圈半徑與大地線在該點的大地方位角的正弦的乘積等半徑與大地線在該點的大地方位角的正弦的乘積等于常數。于常數。 利用這個關系式可以檢查利用這個關系式可以檢查緯度與方位角計算的正確緯度與方位角計算的正確性性coscosaBxrNBW36367.6 7.6 將地面觀測的方向值歸算到橢球面將地面觀測的方向值歸算到橢球面 （重點）（重點）

21、1 1、將地面觀測的水平方向歸算至橢球面、將地面觀測的水平方向歸算至橢球面-三差改正三差改正 歸算中兩個基本要求：歸算中兩個基本要求：（1）以橢球面的法線為基準；）以橢球面的法線為基準；（2）將地面觀測元素化為橢球面上大地線的相應元素。）將地面觀測元素化為橢球面上大地線的相應元素。 將水平方向歸算至橢球面，包括垂線偏差改正、標高差將水平方向歸算至橢球面，包括垂線偏差改正、標高差改正及截面差改正，習慣上稱此三項為改正及截面差改正，習慣上稱此三項為三差改正。三差改正。37371)cossin(ctgZAAmmu 1)cossin(tgAAmm垂線偏差改正的計算公式垂線偏差改正的計算公式 u1）垂線

22、偏差改正）垂線偏差改正 把以垂線為依據的地面觀測的水平方向值歸算到以法線把以垂線為依據的地面觀測的水平方向值歸算到以法線為依據的方向值而應加的改正數稱為為依據的方向值而應加的改正數稱為垂線偏差改正垂線偏差改正。3838h標高差改正：由照準點高度引起的改正標高差改正：由照準點高度引起的改正前面已得出結論：不在同一子午面或不前面已得出結論：不在同一子午面或不在同一平行圈上的兩點的法線是不共面在同一平行圈上的兩點的法線是不共面的。因此，當進行水平方向觀測時，如的。因此，當進行水平方向觀測時，如果照準點高出橢球面某一高度，則照準果照準點高出橢球面某一高度，則照準面就不能通過照準點的法線同橢球面的面就不

23、能通過照準點的法線同橢球面的交點，由此引起的方向偏差的改正稱標交點，由此引起的方向偏差的改正稱標高差改正，以高差改正，以 表示。表示。 h1222222sincos) 1 (2ABHe 22(1)/MaHH常2222221cos) 1 (2BHeK 112sinAKh 照準點大地緯度照準點大地緯度 測站點至照準點的大地方位角測站點至照準點的大地方位角 與照準點的緯度與照準點的緯度B B2 2對對應的子午圈曲率半徑應的子午圈曲率半徑 照準點的覘標高照準點的覘標高 標高差改正主要與照準點的標高差改正主要與照準點的高程有關。高程有關。 3939g3 3）截面差改正）截面差改正將法截弧方向化為大地線方

24、向應加的改正叫將法截弧方向化為大地線方向應加的改正叫截面差改正截面差改正 11221222sincos)2(12ABSeg 11(2)N1221222cos)2(12BSeK 122sinAKg 測站點大地緯度測站點大地緯度 與測站點的緯度與測站點的緯度B B1 1對應的對應的 卯酉圈曲率半徑卯酉圈曲率半徑 截面差改正主要與測站點至照準點截面差改正主要與測站點至照準點間的距離間的距離S S有關。有關。4040各等三角測量在歸算時對取位的要求：各等三角測量在歸算時對取位的要求： 一等需算至一等需算至0.0010.001； 二等為二等為0.010.01； 三等和四等為三等和四等為0.10.1。 在

25、一般情況下，一等三角測量應加三差改正；二等三角在一般情況下，一等三角測量應加三差改正；二等三角測量應加垂線偏差改正和標高改正，而不加截面差改正；三測量應加垂線偏差改正和標高改正，而不加截面差改正；三等和四等三角測量只有在等和四等三角測量只有在 或或H2000mH2000m時，才分時，才分別考慮加垂線偏差改正和標高差改正。別考慮加垂線偏差改正和標高差改正。 01 41412 2、將天文方位角歸化為大地方位角、將天文方位角歸化為大地方位角-起始方位角起始方位角（了解）（了解） ()sinuAL背景：背景：在布設國家天文大地網時，為了控制三角網中方位角傳算誤差的積累，要在布設國家天文大地網時，為了控

26、制三角網中方位角傳算誤差的積累，要求在一等三角鎖的兩端和中央，以及二等網的中間等處，都要在起始邊的兩個端點求在一等三角鎖的兩端和中央，以及二等網的中間等處，都要在起始邊的兩個端點上，用天文觀測的方法測定它們的天文經度、天文緯度和該邊的天文方位角上，用天文觀測的方法測定它們的天文經度、天文緯度和該邊的天文方位角( (包含測包含測站垂線的子午面與測站垂線和照準面所張成的垂直面的夾角站垂線的子午面與測站垂線和照準面所張成的垂直面的夾角) ) 。在特種工程測量控。在特種工程測量控制網中，有時也有這樣的要求。天文方位角是以測站的垂線為依據的，因此必須將制網中，有時也有這樣的要求。天文方位角是以測站的垂線

27、為依據的，因此必須將它歸算至橢球面以測站點相應的法線為依據的大地方位角它歸算至橢球面以測站點相應的法線為依據的大地方位角A A，這種歸算又稱起始方位，這種歸算又稱起始方位角的歸算。角的歸算。 測站點到照準點的大地方位角測站點到照準點的大地方位角測站點處相應方向的天文方位角測站點處相應方向的天文方位角測站點的天文經度測站點的天文經度測站點的大地經度測站點的大地經度測站點的天文緯度測站點的天文緯度垂線偏差改正數垂線偏差改正數 當照準點目標高度不大時，天頂距當照準點目標高度不大時，天頂距Z Z接近于接近于9090時，垂線偏差改正數可勿略時，垂線偏差改正數可勿略不計，因此上式可寫為：不計，因此上式可寫

28、為： ()sinAL 上式又稱為上式又稱為拉普拉斯方程式拉普拉斯方程式，大地方位角又叫拉普拉斯方位角，大地方位角又叫拉普拉斯方位角，在三角點上觀測天文經度、天文緯度時，該點叫拉普拉斯點。在三角點上觀測天文經度、天文緯度時，該點叫拉普拉斯點。 42423 3、觀測天頂距受垂線偏差影響的改正、觀測天頂距受垂線偏差影響的改正（了解）（了解）AAzuzzsincos11 11 11 AAzuzzsincos22 22 22 AAusincos 垂線偏差在測線上的分量：垂線偏差在測線上的分量：A為測站點至照準點的大地方位角。為測站點至照準點的大地方位角。 大地天頂距大地天頂距21ZZ 和的計算公式的計算

29、公式 利用上式公式計算出的大地天頂距利用上式公式計算出的大地天頂距Z Z可用于計算高差，此可用于計算高差，此高差稱為高差稱為大地高差。大地高差。三角高程測量的精度是有限的，若提高三角高程測量的精度是有限的，若提高其計算精度，必須設法克服大氣折光的影響，同時要在天頂其計算精度，必須設法克服大氣折光的影響，同時要在天頂觀測值中引入垂線偏差改正數。觀測值中引入垂線偏差改正數。 43437.7 將地面觀測的長度歸算到橢球面將地面觀測的長度歸算到橢球面（重點）（重點）1 1、基線尺量距的歸算、基線尺量距的歸算 )(22122121HHuuhuusu 1）垂線偏差對長度歸算的影響）垂線偏差對長度歸算的影響

30、 :在基線端點在基線端點1和和2處處垂線偏差在基線方垂線偏差在基線方向上的分量向上的分量 各個測段各個測段測量的高測量的高差總和差總和 基線端點基線端點1和和2處的大處的大地高地高 垂線偏差對長度歸算的影響垂線偏差對長度歸算的影響高程對長度歸算的影響高程對長度歸算的影響此項改正數值一般比較小，是否需要應結合測區及計算此項改正數值一般比較小，是否需要應結合測區及計算精度要求的實際情況進行具體分析。精度要求的實際情況進行具體分析。44442 2）高程對長度歸算的影響：）高程對長度歸算的影響：RHRHRSSmm1010)1(RHSSm基線兩端點平基線兩端點平均大地高程均大地高程 基線方向法截基線方向

31、法截線曲率半徑線曲率半徑 )1 (220RHRHSSmm將上式展開級數，取至二次項將上式展開級數，取至二次項 20002mmHHHSSSSSRR)(2)1 (122110HHuuRHSSm 45452 2、電磁波測距的歸算、電磁波測距的歸算 前提：前提：1) 在橢球面上兩點間大地線長度與相在橢球面上兩點間大地線長度與相應法截線長度之差是極微小的，故可忽略不計，應法截線長度之差是極微小的，故可忽略不計，這樣可將兩點間的法截線長度認為是該兩點間的這樣可將兩點間的法截線長度認為是該兩點間的大地線長度；大地線長度；2) 兩點間的法截線長度與半徑等兩點間的法截線長度與半徑等于其起始點曲率半徑的圓弧長相差

32、也很微小于其起始點曲率半徑的圓弧長相差也很微小(如如當當S=640KM時，之差等于時，之差等于0.3米；米；S=200KM時，之差等于時，之差等于0.005m)。由于工程。由于工程測量中邊長一般為幾公里，最長也不過十幾公里，測量中邊長一般為幾公里，最長也不過十幾公里，因而，這種差異又可忽略不計。因此所求的大地因而，這種差異又可忽略不計。因此所求的大地線長度可以認為是半徑線長度可以認為是半徑RA相應的圓弧長。相應的圓弧長。 232121224)1)(1 ()(1AAARDRHRHDHHDS46462322421AAmRDRHDDhDS由于控制點由于控制點之高差引起之高差引起的傾斜改正的傾斜改正的

33、主項，經的主項，經過此項改正，過此項改正，測線已變成測線已變成平距。平距。由于平均測由于平均測線高出參考線高出參考橢球面而引橢球面而引起的投影改起的投影改正，經過此正，經過此項改正后，項改正后，測線已變為測線已變為弦線。弦線。是由弦長改是由弦長改化為弧長的化為弧長的改正項。改正項。)1)(1 ()(121212AARHRHDHHDd簡化后：簡化后：47477.8 橢球面上三角形的解算橢球面上三角形的解算（重點）（重點）1、用勒讓德爾定理解算球面三角形、用勒讓德爾定理解算球面三角形 假設：假設：半徑為半徑為140KM范圍內的橢球面可當作球面上的一范圍內的橢球面可當作球面上的一部分看待。計算表明：當三角形