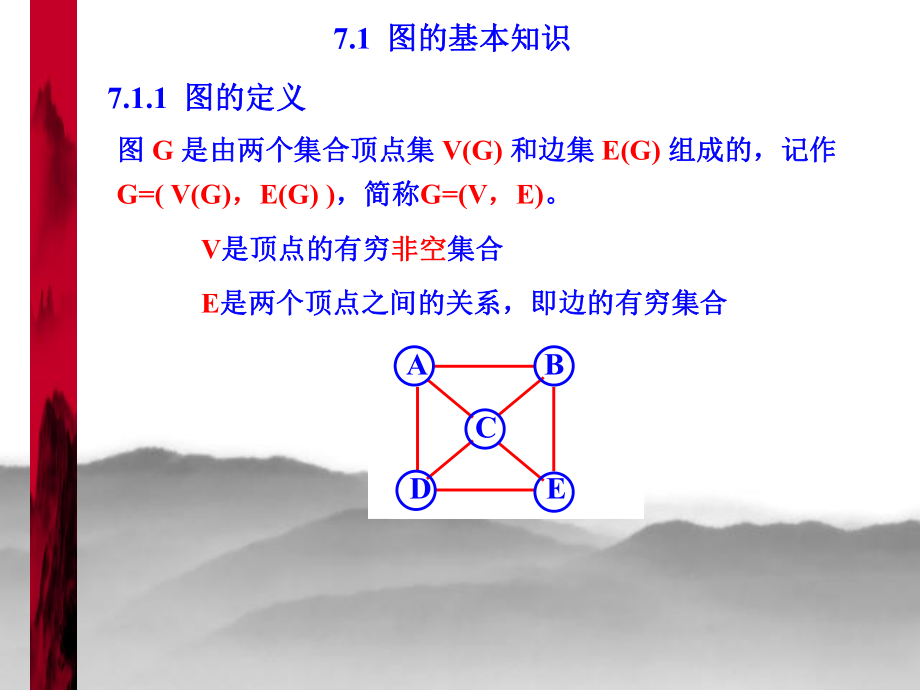
1、數(shù)據(jù)結(jié)構(gòu)（數(shù)據(jù)結(jié)構(gòu)（Java版）版）|第第1章章 緒論緒論|第第2章章 線性表線性表|第第3章章 串串|第第4章章 棧與隊列棧與隊列|第第5章章 數(shù)組和廣義表數(shù)組和廣義表|第第6章章 樹和二叉樹樹和二叉樹第第7章章 圖圖|第第8章章 查找查找|第第9章章 排序排序第七章第七章 圖圖圖是一種較線性表和樹更為復(fù)雜的數(shù)據(jù)結(jié)構(gòu)圖是一種較線性表和樹更為復(fù)雜的數(shù)據(jù)結(jié)構(gòu)。線性表線性表: 線性結(jié)構(gòu)（前驅(qū)、后繼）線性結(jié)構(gòu)（前驅(qū)、后繼）樹樹: 層次結(jié)構(gòu)（父子）層次結(jié)構(gòu)（父子）圖圖: 任意兩個數(shù)據(jù)元素之間都可能相關(guān)（鄰接）任意兩個數(shù)據(jù)元素之間都可能相關(guān)（鄰接） ABCDE7.1 圖的基本知識圖的基本知識圖圖 G 是

2、由兩個集合頂點集是由兩個集合頂點集 V(G) 和邊集和邊集 E(G) 組成的，記作組成的，記作G=( V(G)，E(G) )，簡稱，簡稱G=(V，E)。ABCDEABCDEV是頂點的有窮是頂點的有窮非空非空集合集合 ABCDEE是兩個頂點之間的關(guān)系，即邊的有窮集合是兩個頂點之間的關(guān)系，即邊的有窮集合 7.1.1 圖的定義圖的定義無向圖和有向圖無向圖和有向圖 1. 無向圖無向圖: 邊是頂點的無序?qū)Γ催厸]有方向性。邊是頂點的無序?qū)Γ催厸]有方向性。v1v2v3v5v4V = v1 , v2 , v3 , v4 , v5 E = ( v1 , v2 ) , ( v1 , v4 ) , ( v2 ,

3、 v3 ) , ( v2 , v5 ) , ( v3 , v4 ) , ( v3 , v5 ) ( v1 , v2 )表示頂點表示頂點 v1 和和 v2 之間的邊之間的邊( v1 , v2 ) = ( v2 , v1 )2. 有向圖有向圖: 其邊是頂點的有序?qū)Γ催呌蟹较蛐浴Ｆ溥吺琼旤c的有序?qū)Γ催呌蟹较蛐浴1v2v4v3V = v1 , v2 , v3 , v4 E = , , , 通常有向圖的邊稱為通常有向圖的邊稱為弧弧，表示頂點表示頂點 v1 到到 v2 的弧。的弧。稱稱 v1 為為弧尾弧尾，稱，稱 v2 為為弧頭弧頭。 有有 n(n- -1) 條邊的無向圖稱為條邊的無向圖稱為完全圖完

4、全圖。 12v1v2v4v3有有 n(n-1) 條弧的有向圖稱為條弧的有向圖稱為有向完全圖有向完全圖。 v1v2v33. 完全圖、有向完全圖完全圖、有向完全圖4. 帶權(quán)無向圖帶權(quán)無向圖(無向網(wǎng)無向網(wǎng)) 和和 帶權(quán)有向圖帶權(quán)有向圖(有向網(wǎng)有向網(wǎng))有時對圖的邊或弧賦予相關(guān)的數(shù)值，這種與圖的邊或弧相有時對圖的邊或弧賦予相關(guān)的數(shù)值，這種與圖的邊或弧相關(guān)的數(shù)值叫做關(guān)的數(shù)值叫做權(quán)權(quán)。 帶權(quán)的有向圖稱為帶權(quán)的有向圖稱為有向網(wǎng)有向網(wǎng)。帶權(quán)的無向圖稱為帶權(quán)的無向圖稱為無向網(wǎng)無向網(wǎng)。ABCDE53821497距距離離耗耗費費這種帶權(quán)的圖通常稱為這種帶權(quán)的圖通常稱為網(wǎng)網(wǎng)。 5. 鄰接與關(guān)聯(lián)鄰接與關(guān)聯(lián)對于無向圖對于無

5、向圖 G=(V, E)，如果，如果邊邊 (v, v) E，則稱頂點，則稱頂點 v 和和 v 互為互為鄰接點，即鄰接點，即 v 和和 v 相相鄰接鄰接。 邊邊 (v, v) 依附于頂點依附于頂點 v 和和 v ，或者說，或者說 (v, v) 與頂點與頂點 v 和和 v 相相關(guān)聯(lián)關(guān)聯(lián)。 對于有向圖對于有向圖 G=(V, E) ，如果，如果弧弧 E，則稱頂點，則稱頂點 v 鄰接到鄰接到頂頂點點 v，頂點，頂點 v 鄰接自鄰接自頂點頂點 v 。 vvvv弧弧 和頂點和頂點 v, v 相相關(guān)聯(lián)關(guān)聯(lián)。7.1.2 結(jié)點的度結(jié)點的度對于無向圖，對于無向圖，結(jié)點結(jié)點 v 的度的度是和是和 v 相關(guān)聯(lián)的邊的數(shù)目，

6、記做相關(guān)聯(lián)的邊的數(shù)目，記做TD(v)。 v1v2v3v5v4頂點頂點 v3 的度為的度為 31. 度、入度、出度度、入度、出度對于有向圖，對于有向圖，頂點頂點 v 的的度度 TD(V) 分為兩部分分為兩部分出度出度、入度入度。 以結(jié)點以結(jié)點 v 為為終點終點的弧的數(shù)目稱為的弧的數(shù)目稱為 v 的的入度入度，記為，記為ID(v) ；以結(jié)點以結(jié)點 v 為為起點起點的弧的數(shù)目稱為的弧的數(shù)目稱為 v 的的出度出度，記為，記為OD(v)； 頂點頂點 v 的度的度為為 TD(v) = ID(v) + OD(v)。 v1v2v4v3頂點頂點 v1 的出度為的出度為 2頂點頂點 v1 的入度為的入度為 1頂點頂

7、點 v1 的度為的度為 3性質(zhì)性質(zhì): 對于一個圖對于一個圖(無向圖、有向圖無向圖、有向圖)，如果結(jié)點，如果結(jié)點 vi 的度為的度為TD(vi)，那么具有那么具有 n 個頂點、個頂點、e 條邊或弧的圖，必滿足如下關(guān)系條邊或弧的圖，必滿足如下關(guān)系e = TD(vi)12i = 1n無向圖、有向圖的邊或弧均計算兩遍。無向圖、有向圖的邊或弧均計算兩遍。v1v2v3v5v4v1v2v4v32. 度與邊的關(guān)系度與邊的關(guān)系當(dāng)當(dāng)G為有向圖時，上式可寫為：為有向圖時，上式可寫為： ID(vi)=i = 1ni = 1n OD(vi)=e TD(vi)=i = 1ni = 1nOD(vi)=2ei = 1n ID

8、(vi)+7.1.3 子圖子圖假設(shè)有兩個圖假設(shè)有兩個圖 G=(V, E) 和和 G=(V, E) ，如果，如果 V V，且且 E E，并且，并且EE中的邊所關(guān)聯(lián)的結(jié)點都在中的邊所關(guān)聯(lián)的結(jié)點都在VV中，則中，則稱稱 G 為為 G 的的子圖子圖。 v1v2v4v3求子圖求子圖v1v1v3v1v4v3v1v2v4v3v1v2v4v3v1v2v3v5v4子圖有子圖有v1v2v3v5v1v2v5v4v1v2v3v5v47.1.4 路徑、回路及連通性路徑、回路及連通性無向圖無向圖 G 中若存在一條有窮非空序列中若存在一條有窮非空序列 w = v0 e1 v1 e2 v2 ek vk ，其，其中中 vi 和

9、和 ei 分別為頂點和邊，則稱分別為頂點和邊，則稱 w 是從頂點是從頂點 v0 到到 vk 的一條的一條路徑路徑。頂點頂點 v0 和和 vk 分別稱為路徑分別稱為路徑 w 的的起點起點和和終點終點。路徑的長度路徑的長度是路徑上的是路徑上的邊的數(shù)目邊的數(shù)目。w 的長度為的長度為 kv0v1v2vk- -1vk. . .e1e2ek起點和終點相同且長度大于起點和終點相同且長度大于1的簡單路徑稱為的簡單路徑稱為回路回路。如果在一條路徑中，除起點和終點外，其他結(jié)點都不相同，則此路如果在一條路徑中，除起點和終點外，其他結(jié)點都不相同，則此路徑稱為徑稱為簡單路徑簡單路徑。1. 路徑、路徑長度、回路路徑、路徑

10、長度、回路 帶權(quán)圖中，從起點到終點的路徑上各條邊的權(quán)值之和稱為這條帶權(quán)圖中，從起點到終點的路徑上各條邊的權(quán)值之和稱為這條路徑的路徑長度。路徑的路徑長度。v1v4v529v2v365387 從結(jié)點從結(jié)點v1到到v5的一條路徑（的一條路徑（v1，v4，v5）的路徑長度是）的路徑長度是2+9=11。 一個有向圖一個有向圖G中，若存在一個結(jié)點中，若存在一個結(jié)點v0，從，從v0有路徑可以到達圖有路徑可以到達圖G中其他所有結(jié)點，則稱此有向圖為中其他所有結(jié)點，則稱此有向圖為有根的圖有根的圖，稱，稱v0為圖為圖G的的根根。2. 有根的圖和圖的根有根的圖和圖的根3. 連通圖連通圖無向圖無向圖G，如果從頂點，如果

11、從頂點 v 到頂點到頂點 v 有路徑，則稱有路徑，則稱 v 和和 v 是是連通連通的。的。 如果對于如果對于無向圖無向圖 G 中中任意任意兩個頂點兩個頂點 vi , vj V, vi 和和 vj 都是都是連通連通的，的，則稱則稱 G 是是連通圖連通圖。 v1v2v3v5v4是否為連通圖是否為連通圖連通分量連通分量指的是無向圖中的指的是無向圖中的極大連通子圖極大連通子圖。 ABCLHDEFGH非連通圖非連通圖連通分量為連通分量為ABCLHDEFGH：將圖中：將圖中, ,任何不在連通子圖中的頂點任何不在連通子圖中的頂點, ,加到子圖中后，子圖就加到子圖中后，子圖就。連通圖的連通圖的連通分量是其自身

12、連通分量是其自身而非連通圖而非連通圖可以有多個可以有多個有向圖有向圖G，如果從頂點，如果從頂點 v 到頂點到頂點 v 有路徑有路徑 或或 從頂點從頂點 v 到頂點到頂點 v 有有路徑，則稱路徑，則稱 v 和和 v 是是連通連通的。的。 在在有向圖有向圖 G 中，如果對于每一對中，如果對于每一對 vi, vj V，vivj ，從，從 vi 到到 vj 和和 從從 vj 到到 vi 都都存在路徑，則稱存在路徑，則稱 G 是是強連通圖強連通圖。 v1v2v4v3是否為強連通圖是否為強連通圖4. 強連通圖強連通圖有向圖中的有向圖中的強連通的最大子圖強連通的最大子圖稱作有向圖的稱作有向圖的強連通分量強連

13、通分量。 v1v2v4v3非強連通圖非強連通圖強連通分量強連通分量v2v1v4v3注意注意強連通圖的強連通圖的強連通分量是其自身強連通分量是其自身而非強連通圖而非強連通圖可以有多個可以有多個7.1.5 生成樹生成樹一個連通圖的一個連通圖的是一個極小連通子圖。是一個極小連通子圖。:在極小連通子圖上在極小連通子圖上,任一條邊子圖就任一條邊子圖就,若再若再一條邊一條邊,必定構(gòu)成一個必定構(gòu)成一個。:所有所有n個頂點個頂點;有有n-1條邊條邊;圖是連通的。圖是連通的。V1V2V3V4V5V1V2V3V4V5V1V2V3V4V5圖的圖的生成樹生成樹對非連通圖，則稱由各個連通分量的生成樹的集合為對非連通圖，

14、則稱由各個連通分量的生成樹的集合為此非連通圖的此非連通圖的。性質(zhì)性質(zhì): 一個有一個有n個頂點的連通圖的個頂點的連通圖的生成樹生成樹有且僅有有且僅有n- -1條邊。條邊。1. 如果一棵生成樹有如果一棵生成樹有 n 個頂點和小于個頂點和小于 n- -1 條邊，則為條邊，則為非連通圖非連通圖。2. 如果一棵生成樹有如果一棵生成樹有 n 個頂點和多于個頂點和多于 n- -1 條邊，則一定有條邊，則一定有環(huán)環(huán)。構(gòu)成一棵構(gòu)成一棵 n 頂點生成樹需要頂點生成樹需要 n- -1 條邊，條邊，少于少于 n- -1 ，則必有邊斷開，不再連通。，則必有邊斷開，不再連通。構(gòu)成一棵構(gòu)成一棵 n 頂點生成樹需要頂點生成樹

15、需要 n- -1 條邊，條邊，若再添加一條邊，必會使得與它關(guān)聯(lián)的那兩個頂點之間有了若再添加一條邊，必會使得與它關(guān)聯(lián)的那兩個頂點之間有了第二條路徑。第二條路徑。ABCLHJ性質(zhì)性質(zhì): 一個連通圖的生成樹并不唯一一個連通圖的生成樹并不唯一ABCLHJABCLHJABCLHJ生成樹生成樹ABCLHJ刪除刪除環(huán)環(huán)中的任一條邊中的任一條邊7.2 圖的存儲結(jié)構(gòu)圖的存儲結(jié)構(gòu)順序存儲順序存儲鄰接矩陣鄰接矩陣鏈?zhǔn)酱鎯︽準(zhǔn)酱鎯︵徑颖磬徑颖砣绾伪磉_頂點之間如何表達頂點之間存在的關(guān)系存在的關(guān)系?7.2.1 鄰接矩陣鄰接矩陣設(shè)圖設(shè)圖 G = ( V ，E ) 具有具有 n(n1) 個個頂點頂點 v1 , v2 , ,

16、vn 和和 m 條條邊邊或或弧弧 e1 , e2 , , em ，則，則 G 的鄰接矩陣是的鄰接矩陣是 nn 階矩陣，記為階矩陣，記為 A(G) 。其每一個元素其每一個元素 aij 定義為定義為:鄰接矩陣存放鄰接矩陣存放 n 個個頂點頂點信息和信息和 n2 條條邊邊或或弧弧信息。信息。aij = 01頂點頂點 vi 與與 vj 不相鄰接不相鄰接頂點頂點 vi 與與 vj 相鄰接相鄰接v1v2v4v3例，有向圖例，有向圖 GA(G) = 1 2 3 412340 1 1 00 0 0 00 0 0 11 0 0 0v1v2v3v5v4例無向圖例無向圖 G0 1 0 1 01 0 1 0 10 1

17、 0 1 11 0 1 0 00 1 1 0 0A(G) = 1 2 3 4 512345優(yōu)點優(yōu)點:1. 容易判斷任意兩個頂點之間是否有容易判斷任意兩個頂點之間是否有邊邊或或弧弧。2. 容易求取各個頂點的容易求取各個頂點的度度。鄰接矩陣存儲的圖類鄰接矩陣存儲的圖類public class Graph1 /以鄰接矩陣存儲的圖類以鄰接矩陣存儲的圖類 protected int n； /圖的結(jié)點個數(shù)圖的結(jié)點個數(shù) protected int mat； /二維數(shù)組存儲圖的鄰接矩陣二維數(shù)組存儲圖的鄰接矩陣鄰接矩陣的特點鄰接矩陣的特點1)判斷判斷ViVj間是否有邊間是否有邊(弧弧),只需檢查只需檢查Aij的

18、值是否非的值是否非0。2)很容易計算頂點的度。很容易計算頂點的度。：頂點：頂點Vi 的度為第的度為第i行行(或第或第j列列)的非零元素個數(shù)。的非零元素個數(shù)。: 第第的元素之和是頂點的元素之和是頂點 的的; 第第的元素之和是頂點的元素之和是頂點的的。V0V1V2V3V40 1 0 1 01 0 1 0 10 1 0 1 11 0 1 0 00 1 1 0 0V0V1V2V30 1 1 00 0 0 00 0 0 11 0 0 0例例:0行的行的 元素元素:0, =1表示表示:弧存在弧存在例例:2列的列的 元素元素: , 2=1表示表示:弧存在弧存在無向圖，頂點無向圖，頂點 vi 的的度度是鄰接矩

19、陣中第是鄰接矩陣中第 i 行行或或第第 i 列的元素之和。列的元素之和。例例 G1中，中，v1 的度為的度為 2 ，v2 的度為的度為 3 。v1v2v3v5v4例無向圖例無向圖 G0 1 0 1 01 0 1 0 10 1 0 1 11 0 1 0 00 1 1 0 0A(G) = 1 2 3 4 512345v1v2v4v3例有向圖例有向圖 GA(G) = 1 2 3 412340 1 1 00 0 0 00 0 0 11 0 0 0有向圖，頂點有向圖，頂點 vi 的的出度出度是鄰接矩陣中第是鄰接矩陣中第 i 行行的元素之和。的元素之和。頂點頂點 vi 的的入度入度是鄰接矩陣中第是鄰接矩陣

20、中第 i 列列的元素之和。的元素之和。例例 v1 的度為的度為 2+1=3。無向圖的鄰接矩陣都是無向圖的鄰接矩陣都是對稱矩陣對稱矩陣。有向圖的鄰接矩陣一般有向圖的鄰接矩陣一般不對稱不對稱。1 2 3 412340 1 1 00 0 0 00 0 0 11 0 0 00 1 0 1 01 0 1 0 10 1 0 1 11 0 1 0 00 1 1 0 01 2 3 4 512345無向圖無向圖有向圖有向圖v1v2v3v5v4v1v2v4v3無向圖可以采用無向圖可以采用壓縮存儲方式壓縮存儲方式帶權(quán)圖帶權(quán)圖(網(wǎng)網(wǎng)) 的鄰接矩陣的鄰接矩陣v1v2v3v5v4v65487935651 0 5 7 0

21、4 8 0 9 5 0 6 5 0 A = 1 2 3 4 5 6123456 3 1 0aij = wij若若vi vj，頂點，頂點 vi 與與 vj 相鄰接相鄰接若若vi vj，頂點，頂點 vi 與與 vj 不相鄰接不相鄰接0若若vi= vj7.2.2 鄰接表鄰接表對圖中每一個頂點建立一個單鏈表，指示與該頂點對圖中每一個頂點建立一個單鏈表，指示與該頂點鄰接的鄰接的頂點頂點和和關(guān)關(guān)聯(lián)的聯(lián)的邊邊或或弧弧。data next邊結(jié)點邊結(jié)點datanext頂點結(jié)點頂點結(jié)點data : 結(jié)點數(shù)據(jù)元素信息結(jié)點數(shù)據(jù)元素信息next : 與該結(jié)點關(guān)聯(lián)的另一條邊與該結(jié)點關(guān)聯(lián)的另一條邊data : 頂點的信息頂

22、點的信息next : 第一條關(guān)聯(lián)邊結(jié)點第一條關(guān)聯(lián)邊結(jié)點v1v2v3v5v4e1e2e3e4e5e601234v1v2v3v4v5v4v2v5v3v1v5v4v2v3v1v3v2聲明鄰接表存儲的圖類聲明鄰接表存儲的圖類import ds_java.OnelinkNode; /單向鏈表的結(jié)點類單向鏈表的結(jié)點類public class Graph2 /以鄰接表存儲的圖類以鄰接表存儲的圖類 private OnelinkNode table； /圖的鄰接表圖的鄰接表v1v2v3v5v4無向圖無向圖 Ge1e2e3e4e5e601234v1v2v3v4v5如何獲取頂點的度？如何獲取頂點的度？頂點頂點 v

23、i 的度為第的度為第 i 條鏈中的結(jié)點數(shù)。條鏈中的結(jié)點數(shù)。需要多少存儲空間？（需要多少存儲空間？（n個結(jié)點個結(jié)點m條邊的無向圖）條邊的無向圖）n + 2mv4v2v5v3v1v5v4v2v3v1v3v2無向圖的鄰接表的特點無向圖的鄰接表的特點: 頂點頂點v的的:等于等于v對應(yīng)對應(yīng); 判定兩頂點判定兩頂點v,w 是否是否:看看v對應(yīng)鄰接鏈表中對應(yīng)鄰接鏈表中; 所有鄰接鏈表所有鄰接鏈表;1.在在G中中:要要插入、刪除結(jié)點；插入、刪除結(jié)點；V0V1V2V3V40123431 420 431 20 21 V0V1V2V3V4圖圖G1v1v2v4v3有向圖有向圖 Ge1e2e3e4如何獲取頂點的如何獲取

24、頂點的度度？頂點頂點 vi 的的出度出度為為鄰接表鄰接表第第 i 條鏈中的結(jié)點數(shù)。條鏈中的結(jié)點數(shù)。為了方便求頂點的為了方便求頂點的入度入度，引入引入逆鄰接表逆鄰接表需要多少存儲空間？（只保需要多少存儲空間？（只保留入邊表和出邊表之一）留入邊表和出邊表之一）n + m0123v1v2v3v4頂點頂點 vi 的的入度入度為為逆鄰接表逆鄰接表第第 i 條鏈中的結(jié)點數(shù)。條鏈中的結(jié)點數(shù)。0123v1v2v3v4v3v2v4v1v4v1v1v3鄰接矩陣與鄰接表鄰接矩陣與鄰接表存儲空間存儲空間求頂點的度求頂點的度求頂點的鄰接頂點求頂點的鄰接頂點判斷兩個頂點是否關(guān)聯(lián)判斷兩個頂點是否關(guān)聯(lián)0 1 0 1 01 0

25、 1 0 10 1 0 1 11 0 1 0 00 1 1 0 01 2 3 4 51234501234v1v2v3v4v5v4v2v5v3v1v5v4v2v3v1v3v27.3 圖的遍歷圖的遍歷與樹的遍歷類似，如果從圖中某一頂點出發(fā)，以某種次序順序地與樹的遍歷類似，如果從圖中某一頂點出發(fā)，以某種次序順序地訪問圖中訪問圖中所有頂點所有頂點，且使每一個頂點，且使每一個頂點僅僅被訪問一次，這一過程稱被訪問一次，這一過程稱為為圖的遍歷圖的遍歷。圖的遍歷算法是求解圖的遍歷算法是求解圖的連通性問題圖的連通性問題、生成樹生成樹、和、和拓撲排序拓撲排序等等算法的基礎(chǔ)。算法的基礎(chǔ)。通常有兩條遍歷圖的路徑通常有

26、兩條遍歷圖的路徑: 深度優(yōu)先搜索遍歷深度優(yōu)先搜索遍歷、廣度優(yōu)先搜廣度優(yōu)先搜索遍歷索遍歷。7.3.1 深度優(yōu)先遍歷深度優(yōu)先遍歷深度優(yōu)先搜索（深度優(yōu)先搜索（DFS）遍歷是類似于樹的）遍歷是類似于樹的先序遍歷先序遍歷的一種方法。的一種方法。v1v2v3v5v4v6v7v8圖可分為三部分圖可分為三部分:基結(jié)點基結(jié)點第一個第一個鄰接結(jié)點鄰接結(jié)點所能導(dǎo)出的所能導(dǎo)出的子圖子圖其它其它鄰接頂點所鄰接頂點所能導(dǎo)出的能導(dǎo)出的子圖子圖1 深度優(yōu)先遍歷算法描述深度優(yōu)先遍歷算法描述從圖中選定的一個結(jié)點從圖中選定的一個結(jié)點v0出發(fā)，訪問出發(fā)，訪問v0。 查找與查找與v0有邊相連且未被訪問過的另一個結(jié)點有邊相連且未被訪問過

27、的另一個結(jié)點vj。 若有若有vj，從，從vj出發(fā)繼續(xù)進行深度優(yōu)先搜索遍歷。出發(fā)繼續(xù)進行深度優(yōu)先搜索遍歷。 若找不到若找不到vj，說明從，說明從v0開始能夠到達的所有結(jié)點都已被訪問開始能夠到達的所有結(jié)點都已被訪問過，遍歷結(jié)束。過，遍歷結(jié)束。v1v2v3v5v4v6v7v8過程分析過程分析v1v2v3v4v6v8v5v7深度優(yōu)先搜索順序深度優(yōu)先搜索順序: v1v2v4v8v5v3v6v72 以鄰接矩陣存儲的圖的深度優(yōu)先遍歷算法實現(xiàn)以鄰接矩陣存儲的圖的深度優(yōu)先遍歷算法實現(xiàn) 在以鄰接矩陣存儲的圖在以鄰接矩陣存儲的圖Graph1類中，增加一個一維數(shù)組成員類中，增加一個一維數(shù)組成員變量變量visited和

28、一個成員方法和一個成員方法depthfs()。 visited用于標(biāo)志圖中結(jié)點是否已被訪問。每個數(shù)組元素對應(yīng)用于標(biāo)志圖中結(jié)點是否已被訪問。每個數(shù)組元素對應(yīng)圖的一個結(jié)點，若一個結(jié)點已被訪問，則相應(yīng)的數(shù)組元素被置圖的一個結(jié)點，若一個結(jié)點已被訪問，則相應(yīng)的數(shù)組元素被置為為1，否則為，否則為0。構(gòu)造方法中創(chuàng)建。構(gòu)造方法中創(chuàng)建visited數(shù)組，其元素值全為數(shù)組，其元素值全為0，表示初始狀態(tài)是圖中所有結(jié)點均未被訪問過。表示初始狀態(tài)是圖中所有結(jié)點均未被訪問過。 depthfs()方法實現(xiàn)圖的深度優(yōu)先遍歷算法。方法實現(xiàn)圖的深度優(yōu)先遍歷算法。2以鄰接矩陣存儲的圖的深度優(yōu)先遍歷算法實現(xiàn)以鄰接矩陣存儲的圖的深度優(yōu)

29、先遍歷算法實現(xiàn)package ds_java;public class Graph1 /以鄰接矩陣存儲的圖類 protected int n; /圖的結(jié)點個數(shù) protected int mat; /二維數(shù)組存儲圖的鄰接矩陣 protected int visited; /訪問標(biāo)記數(shù)組 public Graph1(int m1) n=m1.length; mat=new intnn; System.arraycopy(m1,0,mat,0,n); /System類方法，復(fù)制數(shù)組 visited=new int n; public Graph1()【例【例7.1】 以鄰接矩陣表示的圖的深度優(yōu)先遍

30、歷算法測試。以鄰接矩陣表示的圖的深度優(yōu)先遍歷算法測試。import ds_java.Graph1;public class Graph1_ex /圖類的測試圖類的測試 public static void main(String args) int mat1=0,1,0,1, /無向圖無向圖G6的鄰接矩陣的鄰接矩陣 1,0,1,1, 0,1,0,1, 1,1,1,0; Graph1 g1=new Graph1(mat1); g1.depthFirstSearch(); 對于無向圖對于無向圖G6，程序運行結(jié)果如下：，程序運行結(jié)果如下：深度優(yōu)先遍歷深度優(yōu)先遍歷Depth first search：

31、 v1 - v2 - v3 - v4 - v2 - v1 - v4 - v3 - v3 - v2 - v1 - v4 - v4 - v1 - v2 - v3 - 在一個含有在一個含有n個結(jié)點和個結(jié)點和e條邊的圖上進行深度優(yōu)先遍歷，對每個條邊的圖上進行深度優(yōu)先遍歷，對每個結(jié)點，結(jié)點，depthfs()方法至多被調(diào)用一次。因為一旦在一個結(jié)點上調(diào)用方法至多被調(diào)用一次。因為一旦在一個結(jié)點上調(diào)用depthfs()方法，便標(biāo)志該結(jié)點方法，便標(biāo)志該結(jié)點“已被訪問已被訪問”，此后便不再對該結(jié)點，此后便不再對該結(jié)點調(diào)用調(diào)用depthfs()方法。方法。3 以鄰接表存儲的圖的深度優(yōu)先遍歷算法實現(xiàn)以鄰接表存儲的圖的

32、深度優(yōu)先遍歷算法實現(xiàn) 在以鄰接表存儲的圖在以鄰接表存儲的圖Graph2類中，同樣需要成員變量類中，同樣需要成員變量visited數(shù)組和數(shù)組和n，所以，所以Graph2設(shè)計為繼承設(shè)計為繼承Graph1類。類。 構(gòu)造方法中創(chuàng)建具有構(gòu)造方法中創(chuàng)建具有n+1個元素的個元素的table數(shù)組，并將鄰接矩數(shù)組，并將鄰接矩陣陣mat中表示的邊轉(zhuǎn)換成鄰接表中表示的邊轉(zhuǎn)換成鄰接表table中的出邊表。其中，中的出邊表。其中，table0元素不用，使得結(jié)點序號元素不用，使得結(jié)點序號i與與table中的下標(biāo)一致。中的下標(biāo)一致。 output()方法輸出鄰接表方法輸出鄰接表table及其出邊表的各個結(jié)點數(shù)據(jù)元及其出邊表

33、的各個結(jié)點數(shù)據(jù)元素值。素值。depthfs()方法覆蓋超類方法覆蓋超類Graph1中的同名方法。中的同名方法。3以鄰接表存儲的圖的深度優(yōu)先遍歷算法實現(xiàn)以鄰接表存儲的圖的深度優(yōu)先遍歷算法實現(xiàn)import ds_java.OnelinkNode; /單向鏈表的結(jié)點類public class Graph2 extends Graph1 /以鄰接表存儲的圖類 private OnelinkNode table; /圖的鄰接表 public Graph2(int mat) /以鄰接矩陣建立圖的鄰接表 n=mat.length; /繼承Graph1類的成員 table=new OnelinkNoden+1

34、; /建立結(jié)點表，多一個元素 OnelinkNode p=null,q; int i,j; for(i=1;i v2 nulltable2= v2 - v3 - v4 nulltable3= v3 nulltable4= v4 - v1 - v3 null深度優(yōu)先遍歷深度優(yōu)先遍歷Depth first search: v1 - v2 - v3 - v4 - v2 - v3 - v4 - v1 - v3 - v4 - v1 - v2 - v3 -1234567823 28 28 38 38 167 4567 145 【例題】用鄰接表實現(xiàn)深度優(yōu)先搜索【例題】用鄰接表實現(xiàn)深度優(yōu)先搜索例例:已知無向圖

35、的鄰接表如下已知無向圖的鄰接表如下,寫出從頂點寫出從頂點8出發(fā)的出發(fā)的DFS算法的頂點序列。算法的頂點序列。頂點序列頂點序列:DFSAL(8)DFSAL(4)DFSAL(2)DFSAL(1)DFSAL(3)DFSAL(6)84213756DFSAL(7)DFSAL(5)7.3.2 廣度優(yōu)先遍歷廣度優(yōu)先遍歷廣度優(yōu)先搜索（廣度優(yōu)先搜索（BFS）遍歷是類似于樹的）遍歷是類似于樹的層次遍歷層次遍歷的一種方法。的一種方法。v1v2v3v5v4v6v7v8只有父輩結(jié)點只有父輩結(jié)點被訪問后才會被訪問后才會訪問子孫結(jié)點！訪問子孫結(jié)點！把圖人為的分層，把圖人為的分層，按層遍歷。按層遍歷。1 廣度優(yōu)先遍歷算法描述

36、廣度優(yōu)先遍歷算法描述從圖中選定的一個結(jié)點從圖中選定的一個結(jié)點v0作為出發(fā)點，訪問作為出發(fā)點，訪問v0。 將訪問過的結(jié)點將訪問過的結(jié)點v0入隊。入隊。 當(dāng)隊列不空時，進入循環(huán)：當(dāng)隊列不空時，進入循環(huán)： 當(dāng)隊列空時，循環(huán)結(jié)束，說明從當(dāng)隊列空時，循環(huán)結(jié)束，說明從v0開始能夠到達的所有結(jié)開始能夠到達的所有結(jié)點都已被訪問過。點都已被訪問過。 廣度優(yōu)先搜索遍歷類似于樹的層次遍歷。其中必須設(shè)立一個廣度優(yōu)先搜索遍歷類似于樹的層次遍歷。其中必須設(shè)立一個隊列來保存訪問過的結(jié)點，算法描述如下：隊列來保存訪問過的結(jié)點，算法描述如下：u 有結(jié)點有結(jié)點vi出隊。出隊。u 訪問與訪問與vi有邊相連的且未被訪問過的所有結(jié)點有

37、邊相連的且未被訪問過的所有結(jié)點vj。u 訪問過的結(jié)點訪問過的結(jié)點vj入隊。入隊。v1v2v3v5v4v6v7v8過程分析過程分析廣度優(yōu)先搜索順序廣度優(yōu)先搜索順序: v1v2v3v4v5v6v7v8v1v2v3v4v5v6v7v8用隊列實現(xiàn)用隊列實現(xiàn)“廣度優(yōu)先搜索廣度優(yōu)先搜索”的圖示的圖示(1) ,將將vi 作為當(dāng)前頂點作為當(dāng)前頂點;(2)訪問當(dāng)前頂點的訪問當(dāng)前頂點的,并并將這些將這些鄰接結(jié)點作當(dāng)前頂點鄰接結(jié)點作當(dāng)前頂點;(3)重復(fù)步驟重復(fù)步驟(2) 直到圖中直到圖中都被訪問。都被訪問。隊列的作用隊列的作用:頂點被訪問后入隊頂點被訪問后入隊;隊頭出隊訪問其鄰接點。隊頭出隊訪問其鄰接點。隊列隊列Q

38、V0V1V2V3V4V5V6V7起始頂點起始頂點V0V1V2V7V3V4V5V6訪問序列訪問序列:出隊頂點出隊頂點:V0V0V1V2V1V3V4V2V5V6V3V7V4V5V6V72以鄰接矩陣存儲的圖的廣度優(yōu)先遍歷算法實現(xiàn)以鄰接矩陣存儲的圖的廣度優(yōu)先遍歷算法實現(xiàn)import ds_java.Queue2; /鏈?zhǔn)疥犃校仡愋蜑閕nt public void breadthFirstSearch() /圖的廣度優(yōu)先遍歷 /k為起始結(jié)點序號 System.out.println(廣度優(yōu)先遍歷Breadth first search:); for(int k=1;kv2-v4-v3- v2-v1-

39、v3-v4- v3-v2-v4-v1- v4-v1-v2-v3-3以鄰接表存儲的圖的廣度優(yōu)先遍歷算法實現(xiàn)以鄰接表存儲的圖的廣度優(yōu)先遍歷算法實現(xiàn)import ds_java.Queue2; /鏈?zhǔn)疥犃校仡愋蜑閕nt public void breadthfs(int k) /圖的廣度優(yōu)先遍歷 /k為起始結(jié)點序號 int i,j=0; Queue2 q2=new Queue2(); /設(shè)置空隊列 OnelinkNode p; i=k; System.out.print( v+k+ -); /訪問起始結(jié)點 visitedi=1; /設(shè)置訪問標(biāo)記 q2.enqueue(i); /訪問過的結(jié)點入隊

40、while(!q2.isEmpty() /隊列不空時 i=q2.dequeue(); /出隊 if(tablei!=null) /查找有邊相連的另一結(jié)點 對于有向圖對于有向圖G7，程序運行的結(jié)果如下：，程序運行的結(jié)果如下：廣度優(yōu)先遍歷廣度優(yōu)先遍歷Breadth first search: v1 -v2-v3-v4- v2 -v3-v4-v1- v3 - v4 -v1-v3-v2-書面作業(yè)書面作業(yè):分別應(yīng)用分別應(yīng)用 DFS, BFS 實現(xiàn)遍歷實現(xiàn)遍歷 要求盡量按頂點序號順序搜索要求盡量按頂點序號順序搜索2154310861214715131191617181920上機作業(yè)上機作業(yè): 建立一個圖結(jié)

41、構(gòu)，應(yīng)用建立一個圖結(jié)構(gòu)，應(yīng)用DFS或或BFS進行遍歷。進行遍歷。7.4 最小代價生成樹最小代價生成樹7.4.1 樹與圖樹與圖 連通的無回路的無向圖稱為無向樹，簡稱樹。諸連通分連通的無回路的無向圖稱為無向樹，簡稱樹。諸連通分量均為樹的圖稱為森林，樹是森林。量均為樹的圖稱為森林，樹是森林。 由于樹中無回路，因此樹中必定無自身環(huán)也無重邊。若由于樹中無回路，因此樹中必定無自身環(huán)也無重邊。若去掉樹中的任意一條邊，則樹變?yōu)榉沁B通圖；若給樹加上一去掉樹中的任意一條邊，則樹變?yōu)榉沁B通圖；若給樹加上一條邊，則形成圖中的一條回路。條邊，則形成圖中的一條回路。7.4.2 生成樹生成樹1. 生成樹的定義生成樹的定義

42、如果圖如果圖T是無向圖是無向圖G的生成子圖，且的生成子圖，且T是樹，則圖是樹，則圖T稱為圖稱為圖G的的生生成樹成樹。圖。圖G的生成樹的生成樹T包含包含G中的所有結(jié)點和盡可能少的邊。中的所有結(jié)點和盡可能少的邊。 設(shè)圖設(shè)圖G=(V,E)是一個連通的無向圖，從是一個連通的無向圖，從G中的任意一個結(jié)點中的任意一個結(jié)點v0出出發(fā)進行一次遍歷所經(jīng)過的邊的集合為發(fā)進行一次遍歷所經(jīng)過的邊的集合為TE，則，則T=(V,TE)是是G的一個的一個連通子圖，即得到連通子圖，即得到G的一棵生成樹。的一棵生成樹。7.4.2 生成樹生成樹利用利用 DFS 或或 BFS 獲取獲取生成樹生成樹例，例，DFSv1v2v3v5v4

43、v6v7v8v1v2v3v4v6v8v5v7DFS生成樹生成樹例，例，BFSv1v2v3v5v4v6v7v8BFS生成樹生成樹v1v2v3v4v5v6v7v87.4.3 最小代價生成樹最小代價生成樹一個無向圖可以對應(yīng)多個生成樹。一個無向圖可以對應(yīng)多個生成樹。一個帶權(quán)無向圖一個帶權(quán)無向圖(無向網(wǎng)無向網(wǎng))同樣可以對應(yīng)多個生成樹。同樣可以對應(yīng)多個生成樹。一棵一棵生成樹的代價生成樹的代價定義為樹上各邊的權(quán)值總和。定義為樹上各邊的權(quán)值總和。如何求取如何求取最小生成樹最小生成樹？代價最小的生成樹稱為代價最小的生成樹稱為最小生成樹最小生成樹。實際價值？實際價值？v1v2v3v5v4v61556536642v

44、1v2v3v5v4v615342生成樹生成樹v1v2v3v5v4v653642欲在欲在n n個城市間建立通信網(wǎng)，則個城市間建立通信網(wǎng)，則n n個城市應(yīng)鋪個城市應(yīng)鋪n-1n-1條線路；但因為每條線路條線路；但因為每條線路都會有對應(yīng)的經(jīng)濟成本，而都會有對應(yīng)的經(jīng)濟成本，而n n個城市可能有個城市可能有n(n-1)/2 n(n-1)/2 條線路，那么，條線路，那么，如何選擇如何選擇n1n1條線路使總費用最少？條線路使總費用最少？典型用途：典型用途：先建立數(shù)學(xué)模型：先建立數(shù)學(xué)模型：頂點頂點表示城市，有表示城市，有n n個；個；邊邊表示線路，有表示線路，有n1n1條；條；邊的權(quán)值邊的權(quán)值表示線路的經(jīng)濟代價

45、；表示線路的經(jīng)濟代價；連通網(wǎng)連通網(wǎng)表示表示n n個城市間的通信網(wǎng)。個城市間的通信網(wǎng)。顯然此連通網(wǎng)是一顯然此連通網(wǎng)是一棵棵生成樹！生成樹！問題抽象：問題抽象： n n個頂點的生成樹很多，需要從中選一棵個頂點的生成樹很多，需要從中選一棵代價最小代價最小的生成樹，的生成樹，即該樹即該樹各邊的代價之和各邊的代價之和最小。此樹便稱為最小生成樹最小。此樹便稱為最小生成樹MSTMST。7.4.3 最小代價生成樹最小代價生成樹 按照生成樹的定義，按照生成樹的定義，n個結(jié)點的連通圖的生成樹有個結(jié)點的連通圖的生成樹有n個結(jié)點個結(jié)點n-1條邊。因此，構(gòu)造最小生成樹的準(zhǔn)則有條邊。因此，構(gòu)造最小生成樹的準(zhǔn)則有3條：條：

46、 必須只使用該圖中的邊來構(gòu)造最小生成樹。必須只使用該圖中的邊來構(gòu)造最小生成樹。 必須使用且僅使用必須使用且僅使用n-1條邊來連接圖中的條邊來連接圖中的n個結(jié)點。個結(jié)點。不能使用產(chǎn)生回路的邊。不能使用產(chǎn)生回路的邊。7.4.3 最小代價生成樹最小代價生成樹 設(shè)連通帶權(quán)圖設(shè)連通帶權(quán)圖G=(V,E)有有n個結(jié)點和個結(jié)點和m條邊。最初先構(gòu)造一個包條邊。最初先構(gòu)造一個包括全部括全部n個結(jié)點和個結(jié)點和0條邊的森林條邊的森林T=T1,T2,TN，以后每一步向，以后每一步向T中中加入一條邊，它應(yīng)當(dāng)是一端在加入一條邊，它應(yīng)當(dāng)是一端在T的某一棵樹的某一棵樹Ti上、而另一端不在上、而另一端不在Ti上的所有邊中具有最小

47、權(quán)值的邊。由于邊的加入，使上的所有邊中具有最小權(quán)值的邊。由于邊的加入，使T中的某兩中的某兩棵樹合并為一棵，樹的棵數(shù)減棵樹合并為一棵，樹的棵數(shù)減1。經(jīng)過。經(jīng)過n-1步，最終得到一棵有步，最終得到一棵有n-1條邊的最小代價生成樹。條邊的最小代價生成樹。求求MSTMST有多種算法，但最常用的是以下兩種：有多種算法，但最常用的是以下兩種：vKruskalKruskal（克魯斯卡爾）算法（克魯斯卡爾）算法vPrimPrim（普里姆）算法（普里姆）算法 KruskalKruskal算法特點：算法特點：將邊歸并將邊歸并，適于求邊，適于求邊稀疏的網(wǎng)稀疏的網(wǎng)的最小生成樹。的最小生成樹。PrimPrim算法特點算

48、法特點: : 將頂點歸并將頂點歸并，與邊數(shù)無關(guān)，適于，與邊數(shù)無關(guān)，適于邊稠密的網(wǎng)邊稠密的網(wǎng)。對邊操作對邊操作對頂點操作對頂點操作Kruskal 算法算法思想：思想：重復(fù)執(zhí)行重復(fù)執(zhí)行:N = ( V , E ) 是是 n 頂點的連通網(wǎng)，設(shè)頂點的連通網(wǎng)，設(shè) E 是連通網(wǎng)中邊的集合；是連通網(wǎng)中邊的集合； 選取選取 E 中權(quán)值最小的邊中權(quán)值最小的邊 ( u , v ) ，否，否，將邊將邊 ( u , v ) 納入納入 TE 中，并從中，并從 E 中刪除邊中刪除邊 ( u , v ) ；判斷邊判斷邊 ( u , v ) 與與 TE 中的邊是否構(gòu)成回路中的邊是否構(gòu)成回路 ？直至直至 E 為空為空 ；構(gòu)造最

49、小生成樹構(gòu)造最小生成樹 N = ( V , TE )，TE 是最小生成樹中邊的集合，是最小生成樹中邊的集合，初始初始 TE = ；u 和和 v 一定一定不在同一個不在同一個連通分量中連通分量中v1v2v3v5v4v61556536642例，例，v1v2v3v5v4v615342初始初始 TE = 當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v1 , v3 )當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v4 , v6 )當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v2 , v5 )當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v3 , v6 )當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v1 , v4 )當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v3 ,

50、 v4 )當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v2 , v3 )當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v1 , v2 )當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v3 , v5 )當(dāng)前權(quán)值最小邊當(dāng)前權(quán)值最小邊 ( v5 , v6 )Prim 算法算法思想：思想：重復(fù)執(zhí)行重復(fù)執(zhí)行:N = ( V , E ) 是具有是具有 n 個頂點的連通網(wǎng)，設(shè)個頂點的連通網(wǎng)，設(shè) U 是最小生成樹中頂點的是最小生成樹中頂點的集合，設(shè)集合，設(shè) TE 是最小生成樹中邊的集合；是最小生成樹中邊的集合； 初始，初始，U = u1 ，TE = ，在所有在所有 uU，vV- -U 的邊的邊 ( u , v ) 中尋找代價中尋找代價最小最小

51、的邊的邊( u , v ) ，并納入集合并納入集合 TE 中；中；同時將同時將 v 納入集合納入集合 U 中；中；直至直至 U = V 為止。為止。集合集合 TE 中必有中必有 n- -1 條邊。條邊。 v1v2v3v5v4v61556536642例，例，v1v31v25v53v64v42初始初始: U = v1 ，V- -U = v2 , v3 , v4 , v5 , v6 TE = U = v1 , v3 ，V- -U = v2 , v4 , v5 , v6 U = v1 , v3 , v6 ，V- -U = v2 , v4 , v5 重點重點: 邊一定存在于邊一定存在于 U 與與 V-

52、-U 之間。之間。U = v1 , v3 , v4 , v6 ，V- -U = v2 , v5 U = v1 , v2 , v3 , v4 , v6 ，V- -U = v5 U = v1 , v2 , v3 , v4 , v5 , v6 ，V- -U = 算法算法:初始化，初始化，U = v1 ，TE = ；尋求權(quán)值最小邊尋求權(quán)值最小邊 ( u , v )，滿足，滿足 uU & vV- -U；/循環(huán)循環(huán)TE = TE + ；U = U + v ；記錄記錄 v1 到其它各頂點的權(quán)值；到其它各頂點的權(quán)值； /循環(huán)循環(huán)記錄新頂點記錄新頂點 v 到其它各頂點的權(quán)值；到其它各頂點的權(quán)值； /循環(huán)

53、循環(huán)while ( U != V ) return OK ;2. 構(gòu)造最小生成樹構(gòu)造最小生成樹 要求：寫中間過程要求：寫中間過程1245631651062111143318197.5 最短路徑最短路徑蘭州蘭州太原太原北京北京濟南濟南徐州徐州鄭州鄭州西安西安旅客希望停靠站越少越好，則應(yīng)選擇旅客希望停靠站越少越好，則應(yīng)選擇濟南濟南北京北京太原太原蘭州蘭州旅客考慮的是旅程越短越好，則應(yīng)選擇旅客考慮的是旅程越短越好，則應(yīng)選擇1120920720210540340640190濟南濟南徐州徐州鄭州鄭州西安西安蘭州蘭州7.5 7.5 最短路徑最短路徑典型用途：典型用途：交通問題。如：城市交通問題。如：城市A

54、 A到城市到城市B B有多條線路，但每條線路的交有多條線路，但每條線路的交通費（或所需時間）不同，那么，通費（或所需時間）不同，那么，如何選擇一條線路，使總費用（或總?cè)绾芜x擇一條線路，使總費用（或總時間）最少？時間）最少？問題抽象：問題抽象：在在帶權(quán)有向圖帶權(quán)有向圖中中A A點（源點）到達點（源點）到達B B點（終點）的多條路徑中，點（終點）的多條路徑中，尋找一條尋找一條各邊權(quán)值之和最小各邊權(quán)值之和最小的路徑，即最短路徑。的路徑，即最短路徑。（注：最短路徑與最小生成樹不同，路徑上不一定包含（注：最短路徑與最小生成樹不同，路徑上不一定包含n n個頂點）個頂點）兩種常見的最短路徑問題：兩種常見的最

55、短路徑問題：一、一、 單源最短路徑單源最短路徑用用Dijkstra（迪杰斯特拉）（迪杰斯特拉）算法算法二、所有頂點間的最短路徑二、所有頂點間的最短路徑用用Floyd（弗洛伊德）算法（弗洛伊德）算法一頂點到其一頂點到其余各頂點余各頂點任意兩頂任意兩頂點之間點之間7.5.1 從單個源點到其余各頂點的最短路徑算法從單個源點到其余各頂點的最短路徑算法 Dijkstra 算法算法思想思想: 利用已得到的頂點的最短路徑來計算其它頂點的最短路徑。利用已得到的頂點的最短路徑來計算其它頂點的最短路徑。貪心算法貪心算法: 利用局部最優(yōu)來計算全局最優(yōu)。利用局部最優(yōu)來計算全局最優(yōu)。例，例，v5v0v1v4v36010

56、05v21030201050求從求從 v0 到其余各頂點的最短路徑。到其余各頂點的最短路徑。1. 初始，初始，Di 的值為的值為 v0 到到 vi 的弧的權(quán)值的弧的權(quán)值Di 表示表示 v0 到到 vi 的最短路徑的長度的最短路徑的長度顯然，顯然，Di 中的最小值中的最小值 D2 便是便是 v0到到 v2 的最短路徑的長度，的最短路徑的長度，Path2=( v0 , v2 )Pathi表示表示v0 到到 vi 的最短路徑上的頂點的最短路徑上的頂點V1 V2 V3 V4 V5V0Di10301002. 如何尋找下一條最短路徑？如何尋找下一條最短路徑？例，例，v5v0v1v4v3601005v210

57、30201050設(shè)下一條最短路徑的終點是設(shè)下一條最短路徑的終點是 vj ，則，則這條最短路徑或者是這條最短路徑或者是 ( v0 , vj ) 、或、或者是者是 v0 經(jīng)過經(jīng)過 v2 到達到達 vj 的路徑的路徑 ；其中取其中取 Di(D2除外除外) 中的最小值得中的最小值得到到 v4，Path4=( v0 , v4 ) 。3. 如何尋找下一條最短路徑？如何尋找下一條最短路徑？V1 V2 V3 V4 V5V0Di106030100算法描述算法描述假設(shè)用假設(shè)用帶權(quán)的鄰接矩陣帶權(quán)的鄰接矩陣 arcsij 來表示帶權(quán)有向圖。來表示帶權(quán)有向圖。初始，初始，Di 存放存放 v0 到到 vi 各頂點的弧的權(quán)

58、值，各頂點的弧的權(quán)值，Di=arcs0i ，S=；利用公式利用公式 Dj = Min Di | | viV- -S 得到一條新的從得到一條新的從 v0 出發(fā)出發(fā)的最短路徑及新的終點的最短路徑及新的終點 vj ，令，令 S = S + vj ；利用利用 vj 修改從修改從 v0 出發(fā)到集合出發(fā)到集合 V- -S 中任一頂點中任一頂點 vk 可達的路徑的長度可達的路徑的長度 ；Dj + arcsjk 與與 Dk算法時間復(fù)雜度算法時間復(fù)雜度: O(n2)利用已得到的頂點的最短路徑來修改得到其它頂點的更短路徑。利用已得到的頂點的最短路徑來修改得到其它頂點的更短路徑。重復(fù)執(zhí)行重復(fù)執(zhí)行 n- -1 遍，每

59、遍求出一條新的最短路徑遍，每遍求出一條新的最短路徑例，例，v5v0v1v4v3601005v21030201050帶權(quán)鄰接矩陣帶權(quán)鄰接矩陣 10 30 1000 1 2 3 4 5 5 50 10 20 60 012345v21030100v0v2v2106030100v0v4v430v2 , v450 90v0v4v3v350v2 , v4 , v3 60v0v4v3v5v560v2 , v4 , v3 , v5 v1v1v2v3v4v5最短路徑最短路徑新頂點新頂點S頂點頂點路徑長度路徑長度每次修改都用每次修改都用的是最新加入的是最新加入集合集合 S 的頂點的頂點7.5.2 每一對頂點之間的

60、最短路徑算法每一對頂點之間的最短路徑算法 Floyd 算法算法算法算法1: 每次以一個頂點為源頭，重復(fù)執(zhí)行每次以一個頂點為源頭，重復(fù)執(zhí)行 Dijkstra 算法算法 n 遍，便遍，便可得到每一對頂點之間的最短路徑。可得到每一對頂點之間的最短路徑。算法時間復(fù)雜度算法時間復(fù)雜度: O(n3)算法算法2: Floyd 算法算法算法時間復(fù)雜度算法時間復(fù)雜度: O(n3)Floyd 算法思想算法思想初始初始，從圖的，從圖的帶權(quán)鄰接矩陣帶權(quán)鄰接矩陣 D(- -1) 出發(fā)，作為頂點出發(fā)，作為頂點 vi 到到 vj 的最短路徑。的最短路徑。0. 考慮經(jīng)過考慮經(jīng)過 v0 是否會存在更短的路徑，即是否會存在更短的路徑，即