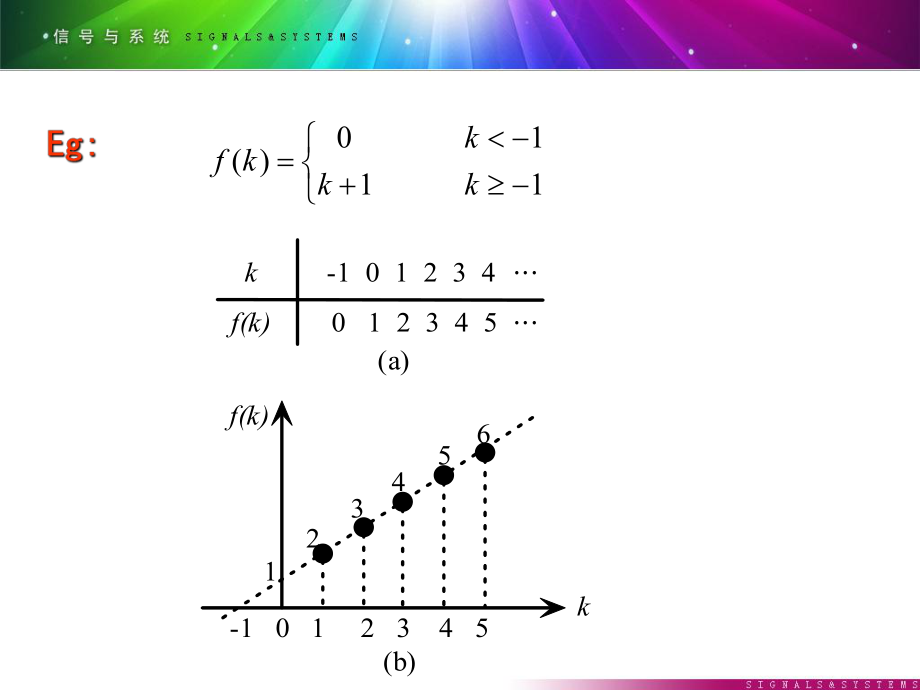
1、1、定義：如果信號僅在一些離散的瞬間具有確定的數值，則稱之為離散時間信號。一般用f(kT)表示，其中k=0,1,2,；T為離散間隔。把這種按一定規則有秩序排列的一系列數值稱為序列，簡記為f(k)。常用序列f(k)表示。 也可以用數據表格形式給出，或以圖形方式表。 1110)(kkkkf k -1 0 1 2 3 4f(k)0 1 2 3 4 5kf(k)123456-1 0 1 2 3 4 5(a)(b)圖 7 - 1（1）相加 ：f(k)=f1(k)+f2(k) （2） 相乘 ： f(k)=f1(k)f2(k) （3）數乘 ：（4）累加和： （1）移位 m為大于零的整數。為大于零的整數。 k

2、f(k)1.50.5-1 0 1 2 3 4 50.51(a)ky(k)=f(k-2)1.50.5 1 2 3 4 5110.5-1 0(b)ky(k)=f(k+2)1.50.5-3 -2 -1 0 1 2110.5-5 -4(c)圖 7 - 3（3）倒相 （4）展縮 需要注意的是需要注意的是，對f(k)進行展縮變換后所得序列y(k)可能會出現k為非整數情況，在此情況下舍去這些非整數的k及其值。 例6.1.1：若x(n)的波形如圖所示，求x(2n) x(n/2)的波形。 還應指出，對于離散信號壓縮后再展寬不能恢復原序列。（5）差分 （a）f(k)的后向差分，記 (b) f(k)的前向差分，記1

3、.單位序列k1(k)圖 7 - 5-1 0 1)()0()()(kfkkf性質：)()()()(mkmfmkkf)()()()(mkmfmkkfk1U(k)圖 7 - 6-1 0 1 2 3 4其他 010 1)(NkkGNk1GN(k)圖 7 - 7-1 0 1 2 3N-1 N4.單邊實指數序列 000)(kkakfk (a為實數) (7-13)k1f(k)=akU(k)|a|1-1 0 1 2 3 4 5k1f(k)=akU(k)|a|1-1 0 1 2 3 4 5(a)(b)圖 7 - 85.正弦序列f(k)E k0 1 23 4 5圖 7 - 9Eg:若離散信號f(k)滿足 則f(k

4、)為周期離散時間信號，其重復周期T=N，重復角頻率為 （1）齊次性、疊加性和線性 當系統 Taf(k)=aTf(k) 則稱系統滿足齊次性。 當系統則稱系統滿足疊加性 當系統同時滿足齊次性和疊加性時，則稱該系統滿足線性 （2）線性離散時間系統 若離散時間系統的響應可分解為零輸入響應和零狀態響應(可分解性)； 且零輸入響應和零狀態響應分別滿足齊次性和疊加性(零輸入線性、零狀態線性)，則稱該系統為線性離散時間系統。 （3）時變與時不變離散時間系統 若 )()(kfTky例6.1.2 若已知k0時三個系統的響應分別為：(1) y(k)=kf(k)； (2) y(k)=|f(k)|；(3) y(k)=2

5、f(k)+3f(k-1)。試判斷這三個系統各為哪類系統。 解解: : (1) 因激勵與響應之間滿足齊次性和疊加性，即但激勵與響應之間不滿足時不變性，即)()()(kykkfkfT )()()()(kaykfaTkakfkafT)()()()()()(212121kykykkfkkfkfkfT)()()()()(mkfmkmkymkkfmkfT故該系統為線性時變離散時間系統(2) 該系統激勵與響應之間不滿足齊次性，不滿足疊加性。激勵和響應之間滿足時不變性，故此系統為非線性時不變系統。 )()()(kaykfTakafT)()()()()()()()(21212121kfkfkykykfkfkfk

6、fT)()()(mkfmkfTmky(3) 由給出的輸入輸出關系可知此系統是一個線性時不變離散時間系統。 解解 :設系統零輸入響應為yx(k)，零狀態響應為yf(k)，則根據線性時不變系統的特性，響應 )()()(kykykyfxkkfxkykfky)3(10)2(12)(2)(2)(例6.1.5：電阻梯形網絡Ev0v1v2vNvN-1v0=E,vN=0,試寫出節點電壓的差分方程。試寫出節點電壓的差分方程。RRRRvN-2RRRR121) 1()()()() 1(RkukuRkuRkuku整理后可得： 0) 1()()2() 1(21kukuRRku或：0)2k(u)1k(u )RR2()k(

7、u21 (b) 加法器(a) 延時器五、 離散時間系統的模擬1、基本運算單元xn xn+ynynE1xnxn-1xnxn-1D D(c) 數乘器axn axnaxn axnaxn axn解解: : 根據系統差分方程，可得1017819176)(232EEEEEEH或 ：32132110178119176)(EEEEEEEH2、系統模擬1/E19f(k)圖 7 - 181/E1/E-8-17-10176y(k)稱之為齊次差分方程 )() 3(2)2()(kukykky(k)1/E1f(k)圖 7 - 191/E1/E2-2241/E-1nknC(常數)特解形式特解形式自由項自由項B （常數）21

8、0121.kkkkCCnC nCnC nnCe()jnAeA為 復 數01CCnjne()ne為實數an(a不是特征根)nC210121()rrnrrCC nC nCnC naan(a是r重特征根)sin(cos)nn或12cossinCnCn2非齊次差分方程0,)2(31)2() 1(32)(kkykkk 對于線性時不變離散時間系統，若激勵為單位序列(k)時，其系統的零狀態響應h(k)稱為單位序列響應。 一、迭代法：是一種遞推法，一個不斷迭代過程，稱之為迭代法 0 0)()() 1()(0kkykfkyaky對于一階系統)()(kkf)() 1()(0kkhakh0)(kh0k)()(khk

9、y令) 1()()(0khakkh)()()(0kUakhk二、等效初值法 當k0時，系統等效為一個零輸入系統。求系統單位序列響應轉化為求系統等效零輸入響應。 例例6.3.1 6.3.1 某離散時間系統如圖所示。求系統單位序列響應。1/Ef(k)圖 7 - 201/E11/2y(k)解：解： 由圖可得系統的差分方程為 )()2(21) 1()(kfkykyky)()(kkf)()2(21) 1()(kkhkhkh0)(kh0k由迭代法可知等效初始值為 當k1時，有0212對應的特征方程為KKCCkh2211)(單位序列響應的形式與零輸入響應形式相同6.4 6.4 卷積和卷積和一、離散系統的時域

10、分解0)()()(iikifkfkf(k) 62 1 2 3 4 5 6 7442-1 0圖 7 - 21)5(2)4(4)3(6)2(4) 1(2)(kkkkkkf1、交換律、結合律和分配律（1）交換律卷積和的性質：12122121 mmx nx nx m x nmx m x nmx nx n12122121 mmx nx nx m x nmx m x nmx nx n二、 卷積和 設兩個離散時間信號為f1(k)和f2(k) ，定義f1(k)與f2(k)的卷積和運算為 （2）結合律 123123 x nx n x nx n x nx n（3）分配律 1231213 x nx nx nx n

11、x nx n x n2 2、移位性質、移位性質12112212 y nx nx nx n nx n ny n nn若則3、其它性質00 xnn nxn n xnnxn nmmxn unxmun mxm4、卷積和的計算： my nx m h nm（1）圖解法反褶、平移、相乘、求和四個步驟：例例6.4.26.4.2 描述離散時間系統的差分方程為 已知y(-1)=1,求系統全響應y(k)。 )(05. 0) 1(9 . 0)(kUkyky解:(1) 求零輸入響應yx(k)。 1) 1(0) 1(9 . 0)(xxxykykykxCky)9 . 0()(得C=0.9,故 1)9 . 0()(kxky(2) 求單位序列響應。 0 0)()(05. 0) 1(9 . 0)(kkhkkhkh利用等效初值法，可求得 )()9 . 0(05. 0)(kUkhk(3) 求激勵時零狀態響應。 )(