1、弧長和扇形面積教學設計 張地營子鄉學校 2013-11-19弧長與扇形的面積教學設計 授課內容：弧長與扇形的面積 節次：24.4.1，第1課時一、教學任務分析教學目標知識技能認識扇形，會計算弧長和扇形的面積，通過弧長和扇形面積的發現與推導，培養學生運用已有知識探究問題獲新知識的能力。數學思考通過思考問題，培養學生動腦的好習慣解決問題師生互動，共同解決問題情感態度通過弧長和扇形面積的發現與推導，培養學生運用已有知識探究問題獲得新知的能力。重點弧長和扇形面積公式，準確計算弧長和扇形的面積。難點運用弧長和扇形的面積公式計算比較復雜圖形的面積。 二、教學流程安排活動流程圖活動內容和目的創設情景思考問題

2、試一試例題講解課堂小結布置作業思考問題后試一試，再講，再做，讓學生逐步掌握對所學知識的應用三、教學過程設計問題與情境師生行為設計意圖制造彎形管道時，經常要先按中心線計算“展直長度”再下料，這就涉及到計算弧長的問題學生分組討論、思考創設情境，引出問題思考1:（1）半徑為R的圓,周長是多少？（2）圓的周長可以看作是多少度的圓心角所對的弧？（3）1°圓心角所對弧長是多少？ 若設O半徑為R， n°的圓心角所對的弧長為L ，則 師生互動，共同解決問題出示思考問題，讓學生養成思考問題的習慣（4）140°圓心角所對的弧長是多少？師生互動，共同解決問題出示思考問題，培養學生運用知

3、識解決問題的能力。例1、 已知圓弧的半徑為50厘米，圓心角為60°，求此圓弧的長度。例2、制造彎形管道時，要先按中心線計算“展直長度”，再下料，試計算圖所示管道的展直長度L(單位：mm，精確到1mm)教師分析方法，學生自己整理并寫出解題過程通過講解例題，使學生進一步提高學生運用知識分析問題、解決問題的能力。扇形定義：由組成圓心角的兩條半徑和圓心角所對的弧所圍成的圖形叫扇形思考2:（1）半徑為R的圓,面積是多少？（2）圓面可以看作是多少度的圓心角所對的扇形？（3）1°圓心角所對扇形面積是多少？ 若設O半徑為R， n°的圓心角所對的扇形面積為S，則 師生共同解決給學生

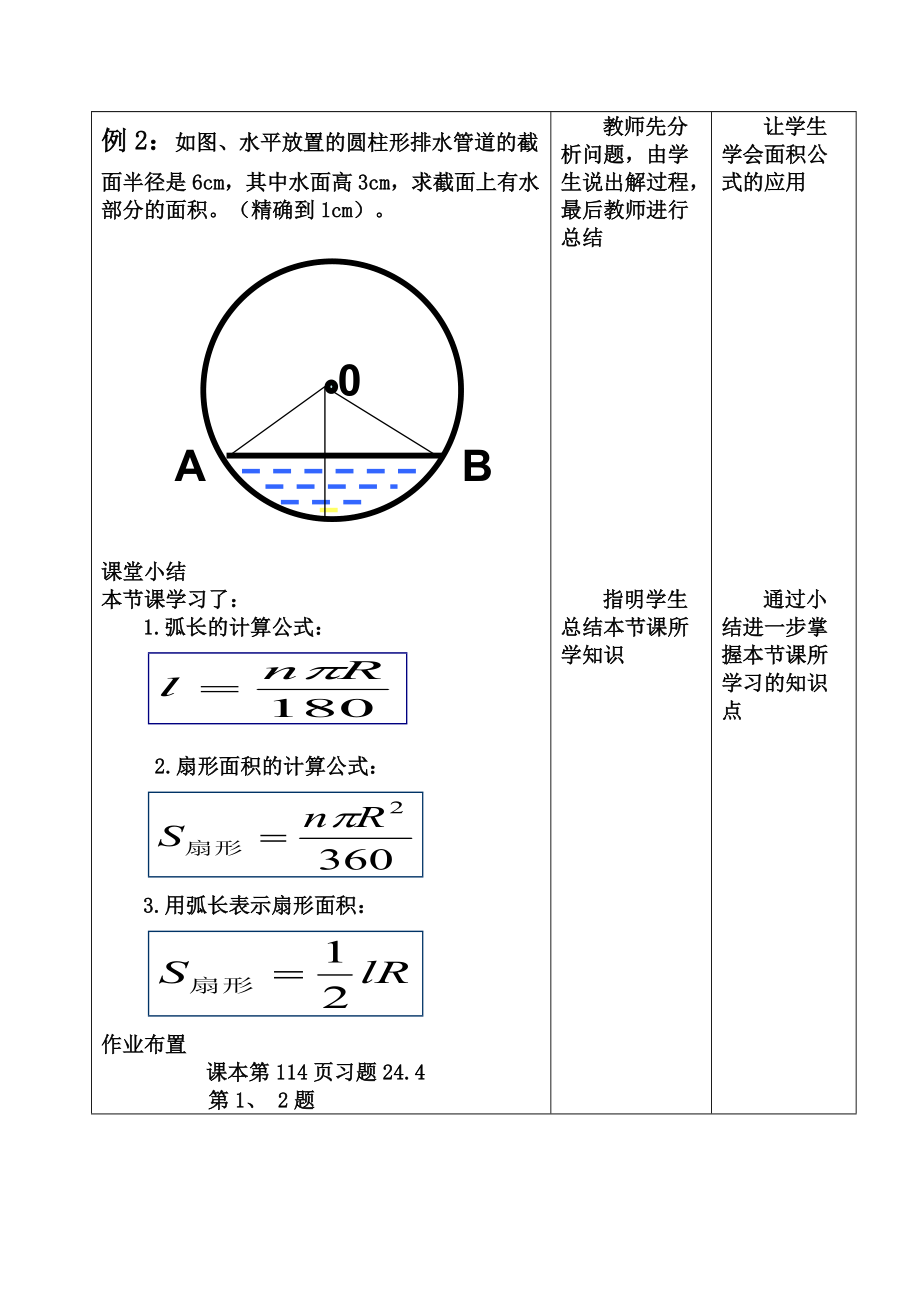
4、一個思考的機會探索弧長與扇形面積的關系比較扇形面積(S)公式和弧長(l)公式,你能用弧長來表示扇形的面積嗎?想一想：扇形的面積公式與什么公式類似？ 做一做：1、已知扇形的圓心角為120°，半徑為2，則這個扇形的面積S扇形= .2、已知半徑為4的扇形，面積為 ，則它的圓心角的度數為_ 3、已知扇形的弧長為10 半徑為4，則這個扇形的面積為_例2：如圖、水平放置的圓柱形排水管道的截面半徑是6cm，其中水面高3cm，求截面上有水部分的面積。（精確到1cm）。 0BA 課堂小結本節課學習了：1.弧長的計算公式： 2.扇形面積的計算公式： 3.用弧長表示扇形面積： 作業布置課本第114頁習題24.4 第1、 2題小組討論，教師引導，得出用弧長和半徑求扇形面積度方法分組練習，交換檢查出錯原因，并進行糾正教師先分析問題，由學生說出解過程，最后教師進行總結指明學生總結本節課所學知識發展學生創新思維的能力讓學