1、 1 1 直線的投影直線的投影 3 3 兩直線的相對位置兩直線的相對位置 4 4 一邊平行于投影面的直角一邊平行于投影面的直角的投影的投影目錄 2 2 直線上的點直線上的點aabbb ba aV VWWHHZ ZX XO OY YV VZ ZX XY YO OWWHHA AB Bbbaaa ab bb ba aHHWWV VO OZ ZY YX X1. ab1. ab積聚為一點積聚為一點. .3. a3. ab b=ab=AB.=ab=AB.1. a1. ab b積聚為一點積聚為一點. .3. ab=ab=AB.3. ab=ab=AB.1. ab1. ab積聚為一點積聚為一點. .3. ab=

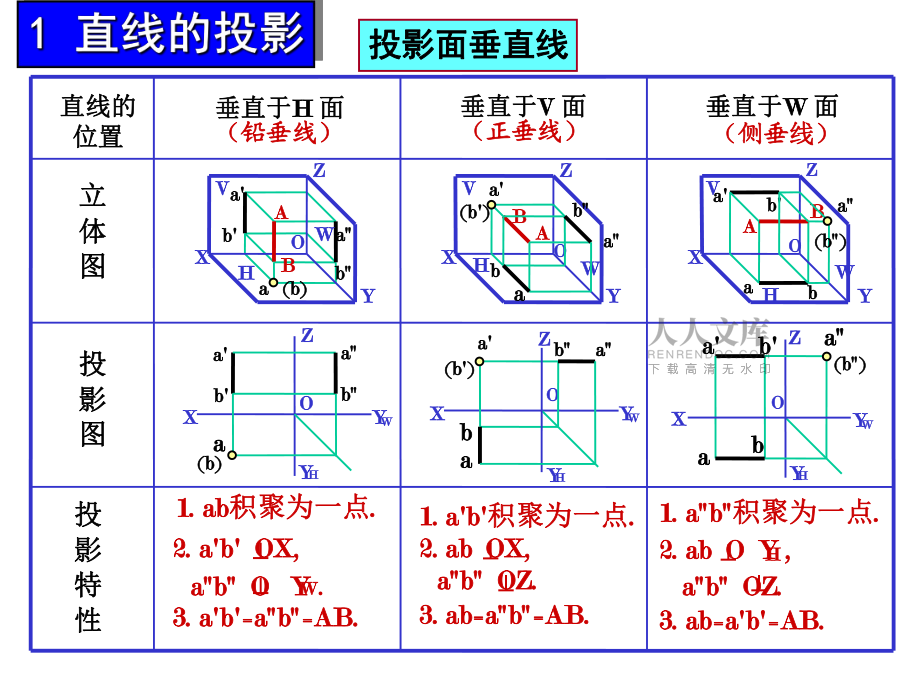
2、a3. ab=ab b=AB.=AB.投影面垂直線投影面垂直線立立 體體 圖圖投投 影影 圖圖投投 影影 特特 性性直線的直線的 位置位置垂直于垂直于H H 面面（鉛垂線鉛垂線）垂直于垂直于V V 面面（正垂線正垂線） 垂直于垂直于W W 面面 （側垂側垂線）線）Y YHHZ Zb bX Xa aY YO Oa a(b)(b)WWaabbA AB B2. ab OX,2. ab OX, ab OZ.ab OZ.HH2. ab O Y ,2. ab O Y , ab OZ.ab OZ.WW2. a2. ab b OX, OX, ab O Yab O Y .A AB BY YZ ZO OX Xa

3、a(b(b) )b ba aaabbHHY YWWa a (b)(b)a a(b(b) )Y YHHO O(b)(b)aaX Xb ba ab ba aZ ZY YWW(b)(b)aa投影面垂直線a ab b投影面平行線投影面平行線1. ab=AB;1. ab=AB;a ab b OZ. OZ.2. ab OY ,2. ab OY , H H1. a1. ab b=AB;=AB;2. ab OX,2. ab OX, ab OZ.ab OZ.1. ab=AB1. ab=AB; ;2. a2. ab b OX OX ab OYab OYWW . .O OZ ZY YHHb baaa aa ab b

4、X XY YWWbbX XY YWWa ab ba ab baabbZ ZY YHHO O立立 體體 圖圖投投 影影 圖圖投投 影影 特特 性性直線的直線的 位置位置平行于平行于H H 面面（水平線水平線）平行于平行于V V 面面（正平正平線）線） 平行于平行于W W 面面 （側平線側平線）Z ZV VY YX XO OHHWWbbaaa ab ba ab bZ ZV VX XY YO OHHWWa ab bb ba aA AB Ba ab bZ ZV VX XY YHHWWO Oa ab bbbaaA AB BaabbY YHHY YWWX Xb ba aaaa ab bZ ZO ObbA

5、AB B投影面平行線A AB BC CD DE E(F)(F) 例例 判斷形體中的輪廓線與投影面的相對位置判斷形體中的輪廓線與投影面的相對位置a ad db bc cd dbbc ce(f)e(f)b b(e (e) )c c(f (f) )a(e)a(e)d(f)d(f)a aEFEF是鉛垂線是鉛垂線CFCF是正垂線是正垂線DFDF是側垂線是側垂線CDCD是水平線是水平線ADAD是正平線是正平線BCBC是側平線是側平線例一般位置直線一般位置直線 1. 與三個投影面都傾斜的直線稱為與三個投影面都傾斜的直線稱為一般位置直線一般位置直線。 2. 投影特性：三個投影長度均小于實長，并傾斜于投影投影特

6、性：三個投影長度均小于實長，并傾斜于投影軸，且不反映與投影面的傾角。軸，且不反映與投影面的傾角。(直線與直線與H H面的傾角記為面的傾角記為 , ,與與V V面的傾角記為面的傾角記為 , ,與與W W面的傾角記為面的傾角記為 。) ) a ab bbbaaa ab bB BA Ao oZ ZX XY YV VWWHHHHY YZ ZX Xo oWWY Ya aa ab bb bbbaa一般線用用直角三角形法直角三角形法求求一般位置一般位置 直線直線的的實長實長 以以H H（V V、W W）投影）投影長為一直角邊，兩端點長為一直角邊，兩端點的的Z Z（Y Y、X X）坐標差為）坐標差為另一直角邊

7、，作一直角另一直角邊，作一直角三角形，則斜邊長為實三角形，則斜邊長為實長。長。a ab bbbaaa ab bB BA Ao oZ ZX XY YV VWWHHHHY YZ ZX Xo oWWY Y實 長a aa ab bb bbbaaH投影長實 長Y YY YX X X X實 長Z ZZ Z直角三角形的構成：直角三角形的構成：投影長、坐標差、傾角、投影長、坐標差、傾角、實長。實長。直角三角形法a a b b a ab b直線上的點直線上的點直線上的點直線上的點的投影，一定落在該直線的同面投影上。直線上的點的投影，一定落在該直線的同面投影上。o oZ ZX XY YV VWWHHA AB Ba

8、 ab bb ba ac c c c一直線上兩線段長度之比，等于它們的投影長度之比。一直線上兩線段長度之比，等于它們的投影長度之比。AC:CB=ac:cb=aAC:CB=ac:cb=ac c:c :c b bC Cc cc co oZ ZX XY YV VWWHH例：直線上取點直線上的點直線上的點 例例 在在AB線上求一點線上求一點C，使點，使點C與與V、H等距。等距。a ab ba ab bb ba ab bA AB Bbbaaa aaabbc cc c 作作V-HV-H平面的分角面（此面垂直于平面的分角面（此面垂直于W W面，積聚為一條面，積聚為一條4545線，面上所有的點均與線，面上所有

9、的點均與V V、H H等距），求出等距），求出ABAB的的W W投影與此投影與此4545線的交點即得。線的交點即得。c c4545c c分角面分角面與與H面面距離距離與與V面面距離距離c cc cC C 兩直線平行兩直線平行a a b bd dc cX XO Oa ab bd dc ca ab bd dc cD DA AC CB Ba ab bc cd dHHV VO OX X 空間平行兩直線，空間平行兩直線，其同面投影仍互相平其同面投影仍互相平行。行。 反之，若兩直線的反之，若兩直線的同面投影同面投影都都互相平行，互相平行，則這兩直線平行。則這兩直線平行。 判斷兩條一般線是否判斷兩條一般線是

10、否平行，要畫全它們的三面投平行，要畫全它們的三面投影。當且僅當，其三面投影影。當且僅當，其三面投影分別平行，才能判斷兩直線分別平行，才能判斷兩直線在空間處于平行狀態。否則，在空間處于平行狀態。否則，兩直線不平行。兩直線不平行。ABAB CDCDabab cdcd; ; a ab b c cd d e ef fe ee ef ff fm mm mn nn nmmnnX XO OY YY YZ ZWWHHEF EF MNMN? ?EFEF MNMN兩直線平行 兩直線相交兩直線相交相交兩直線，其同相交兩直線，其同面投影均相交，且面投影均相交，且交點的連線垂直于交點的連線垂直于投影軸。投影軸。反之，反

11、之，若兩直線的同面投若兩直線的同面投影均相交，影均相交，且交點的連線且交點的連線垂直于投影軸，則垂直于投影軸，則兩直線兩直線相交。相交。若兩直線中有一條為某一若兩直線中有一條為某一投影面的平行線，則應利投影面的平行線，則應利用第三投影來進行判斷。用第三投影來進行判斷。( (本例中本例中和和點不是交點，點不是交點，因此，因此，AB與與CD不相交。不相交。) )A AB Bb ba aa ab bc cd dc cd dX XO Oa ab ba ab bc cd dc cd dHHV VO OX XC CD DK Kk k k kk kk ka ab ba aaabbb bX XO OY YY

12、YZ ZWWHHc cd dc cd dc cdd AB與與CD不相交不相交兩直線相交兩直線交叉 兩直線交叉兩直線交叉既不平行、也不相交的兩直線稱為既不平行、也不相交的兩直線稱為交叉兩直線交叉兩直線。交叉二直線的同面投影可能平行，但不可能所有同面投交叉二直線的同面投影可能平行，但不可能所有同面投影都平行；其同面投影可能相交，但交點連線不垂直于影都平行；其同面投影可能相交，但交點連線不垂直于投影軸。投影軸。b ba aa ab bc cd dc cd dV VHHO OX XA AB BD DC CF FE Ee e(f)(f)g g(j (j) )G GJ J重影點 兩直線交叉兩直線交叉 比較

13、相鄰投影兩點的坐標大小，坐標大比較相鄰投影兩點的坐標大小，坐標大的可見，坐標小的不可見。的可見，坐標小的不可見。Y YG G Y YJ Jg g可見可見j j不可見不可見Z ZE E Z ZF Fe e可見可見f f不可見不可見g g(j (j) )c cd dd dc cb ba aa ab bO OX Xg gj je e(f)(f)e ef f重影點重影點重影點重影點重影點的可見性判斷重影點的可見性判斷：b ba aa ab bc cd dc cd dV VHHO OX XA AB BD DC CF FE Ee e(f)(f)g g(j (j) )G GJ J重影點重影點：分屬兩直線的兩

14、個點在某投影面上的重合投影叫重影點。：分屬兩直線的兩個點在某投影面上的重合投影叫重影點。 兩直線垂直兩直線垂直空間兩直線空間兩直線相交（或交叉）垂直相交（或交叉）垂直，當一直線（或兩直線）平，當一直線（或兩直線）平行于某投影面時，它們在該投影面上的投影才反映直角。行于某投影面時，它們在該投影面上的投影才反映直角。反之，反之，若兩直線在某投影面上的投影為直角，而且其中一條若兩直線在某投影面上的投影為直角，而且其中一條直線平行于該投影面，則這兩條直線在空間一定相互垂直。直線平行于該投影面，則這兩條直線在空間一定相互垂直。X XO OV VHHO OX Xc cC Cc ca ab ba ab bB

15、 BA Ac cc cb bb ba aa ac c1 1b b1 1( (c c1 1) )B B1 1C C1 1(b)(b)c c1 1b b1 1(c)(c)(b)(b)ABAB與與BCBC相交垂相交垂直直ABAB與與B B1 1C C1 1交叉垂交叉垂直直兩直線垂直例例 判斷下列各題的兩直線是否垂直（相交或交叉）。判斷下列各題的兩直線是否垂直（相交或交叉）。（相交不垂直）（相交不垂直）c cd dd dc cX XO Oa aa ab bb bO OX Xa ab ba ab bc cd dc cd da ab ba ab bd dc cc cd dX XO Oa ab ba ab bX XO Oc cd dc cd d（交叉垂直交叉垂直）（交叉垂直）（交叉垂直）（相交