1、前言前言第一節第一節 晶體結構的周期性晶體結構的周期性 第二節第二節 一些晶格的舉例一些晶格的舉例 第三節第三節 晶面、晶向和它們的標志晶面、晶向和它們的標志 第四節第四節 倒格子倒格子第五節第五節 晶體的對稱性晶體的對稱性一、布拉伐格子一、布拉伐格子二二 、原胞、原胞三、三、 晶胞晶胞( (單胞單胞) )一、布拉伐格子一、布拉伐格子表征了晶格的周期性表征了晶格的周期性理想晶體：可看成是由完全相同的理想晶體：可看成是由完全相同的基本基本結構單元結構單元 （）在空間作周期性無限排列構成）在空間作周期性無限排列構成單個原子單個原子或或離子離子或若干個或若干個原子的集團原子的集團：代表：代表基元中空

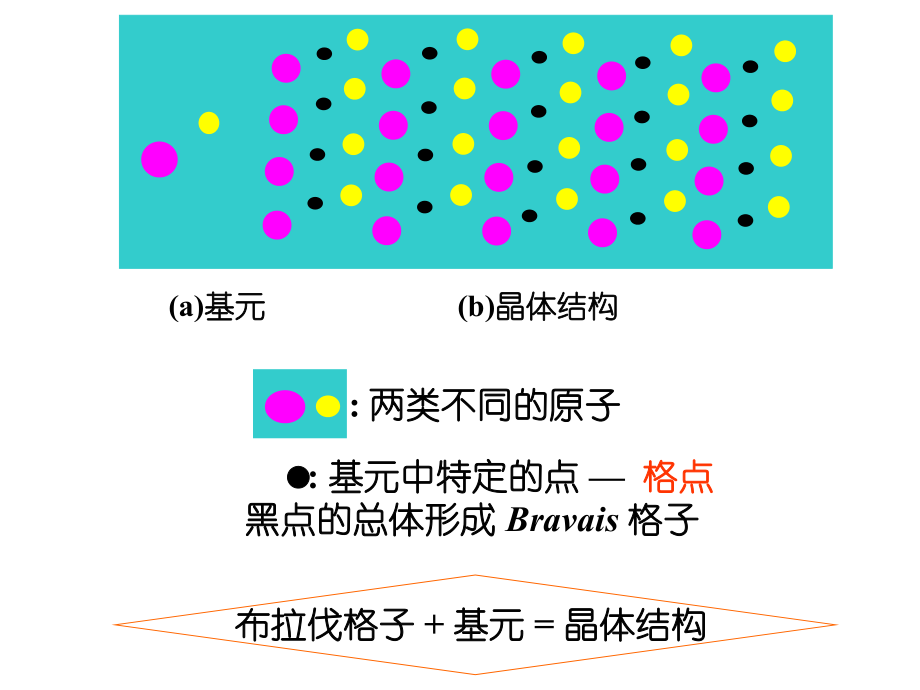
2、間位置基元中空間位置的點稱為的點稱為格點格點 一切格點是等價的一切格點是等價的每個格點的周圍每個格點的周圍環環 境相同境相同因為因為一切一切基元的基元的組成組成，位相位相和和取取 向向都相同都相同等價數學定義：等價數學定義： 中中取一切整數值取一切整數值所所確定的點確定的點 的集合稱為布拉伐格子。的集合稱為布拉伐格子。332211alalalRl用用一個點一個點 來代表基元中的空間位置（例如：基元的來代表基元中的空間位置（例如：基元的重心），這些呈周期性無限分布的幾何點的集合形重心），這些呈周期性無限分布的幾何點的集合形成成 的空間點陣的空間點陣(a)基元基元 (b)晶體結構晶體結構布拉伐格子

3、布拉伐格子 + 基元基元 = 晶體結構晶體結構: 兩類不同的原子兩類不同的原子: 基元中特定的點基元中特定的點 格點格點黑點的總體形成黑點的總體形成 Bravais 格子格子注意事項：注意事項：1）一個布拉伐格子基矢的取法不是唯一的）一個布拉伐格子基矢的取法不是唯一的：若在布拉伐格子中取格點為原點，它至其：若在布拉伐格子中取格點為原點，它至其 他格點的矢量他格點的矢量 稱為格矢量。可表示為稱為格矢量。可表示為 ，為為 一組一組332211alalalRl321,aaalR1234二維布拉伐格子幾種可能的基矢和原胞取法二維布拉伐格子幾種可能的基矢和原胞取法2）不同的基矢一般形成不同的布拉伐格子）

4、不同的基矢一般形成不同的布拉伐格子晶系晶系軸和角度軸和角度布拉伐格子布拉伐格子斜方斜方a b 90簡單斜方簡單斜方長方長方a b = 90簡單長方簡單長方中心長方中心長方正方正方a = b = 90簡單正方簡單正方六角六角a = b=120簡單六角簡單六角baababba簡簡單單三三斜斜簡簡單單單單斜斜底底心心單單斜斜簡簡單單正正交交底心底心正交正交面面心心正正交交體體心心正正交交簡單簡單四方四方簡簡單單菱菱方方體體心心四四方方簡單簡單六方六方簡簡單單立立方方體體心心立立方方面面心心立立方方二二 、原胞、原胞所有晶格的共同特點所有晶格的共同特點 具有具有周期性周期性（平移對稱性平移對稱性）1、

5、 定義：定義：一個晶格：一個晶格最小的周期性單元最小的周期性單元，也稱為，也稱為固體固體物理學物理學原原胞胞:指原胞的邊矢量，一般用指原胞的邊矢量，一般用 表示表示321,aaa用用原胞原胞和和基矢基矢來描述來描述描描述述方方式式位置坐標描述位置坐標描述2 2 、注意、注意： 三維晶格原胞三維晶格原胞( (以基矢以基矢 為為棱的平行六面體棱的平行六面體 是晶格體積的最小重復單元）是晶格體積的最小重復單元） 的體積的體積 為：為：321,aaa二維晶格原胞的面積二維晶格原胞的面積為：為：21aaS一維晶格原胞的長度一維晶格原胞的長度為最近鄰布拉伐格點的間距為最近鄰布拉伐格點的間距321.aaa原

6、胞的取法原胞的取法不是唯一不是唯一的（基矢取法的非唯一性）的（基矢取法的非唯一性）平行六面體形原胞平行六面體形原胞 固體物理學原胞固體物理學原胞，有時難反映有時難反映晶格的全部宏觀晶格的全部宏觀對稱性對稱性性質：每個原胞有性質：每個原胞有原子原子 所有原子完全所有原子完全“等價等價 ”舉例：具有體心立方晶格的舉例：具有體心立方晶格的堿金屬具有堿金屬具有面心立方結構面心立方結構的的 AuAu, , AgAg, ,CuCu 晶體晶體3 3、 晶格分類晶格分類CsCl 結構結構NaCl晶格結構的典型單元晶格結構的典型單元性質性質：每個原胞包含：每個原胞包含的原子的原子實際上實際上表示表示晶格包含兩種

7、或更多種等價的原子或離子晶格包含兩種或更多種等價的原子或離子結構結構：每一種等價原子形成一個簡單晶格每一種等價原子形成一個簡單晶格; ; 不同等價原子形成的簡單晶格是相同的不同等價原子形成的簡單晶格是相同的由若干個相同的由若干個相同的相對錯位套構而成相對錯位套構而成舉例：舉例：NaCl，CsCl包含兩種等價離子包含兩種等價離子所有原子都是一樣的所有原子都是一樣的六角密排晶格結構六角密排晶格結構 Be,Mg,Zn金剛石晶格結構金剛石晶格結構 C,Si,Ge六角密排晶格結構的典型單元六角密排晶格結構的典型單元ABca復式晶格的原胞：就是相應的復式晶格的原胞：就是相應的簡單晶格的原胞，簡單晶格的原胞

8、，在原胞中包在原胞中包含了每種等價原子各一個含了每種等價原子各一個。、位置坐標描述晶格周期性：、位置坐標描述晶格周期性：簡單晶格簡單晶格：每個原子的位置坐標：每個原子的位置坐標： 332211alalal321,aaa為晶格基矢為晶格基矢321,lll為一組整數為一組整數每個原子的位置坐標：每個原子的位置坐標：復式晶格復式晶格：332211alalalri,.,2 , 1 : 原胞內各種等價原子之間的相對位移原胞內各種等價原子之間的相對位移ar面心立方位置的原子面心立方位置的原子 B 表示為：表示為：332211alalal立方單元體內對角線上的原子立方單元體內對角線上的原子 A 表示為表示為

9、:332211alalal其中其中 為為 1/4 體對角線體對角線金剛石晶格結金剛石晶格結構的典型單元構的典型單元構成構成：由面心立方單元的：由面心立方單元的中心到頂角中心到頂角引引8條對角線，在其中條對角線，在其中互不相鄰的互不相鄰的4 4條對角線的中點條對角線的中點，各加一個原子，各加一個原子 得到金剛石晶格結構！得到金剛石晶格結構！特點特點：每個原子有：每個原子有4 4個最近鄰個最近鄰，它們正，它們正好在好在正四面體正四面體的頂角位置！的頂角位置！三、三、 晶胞晶胞( (單胞單胞) )：為反映晶格的對稱性，在結晶學中選擇：為反映晶格的對稱性，在結晶學中選擇較大較大 的周期單元的周期單元稱

10、為稱為晶體學原胞晶體學原胞：沿晶胞的三個棱所作的三個矢量，常：沿晶胞的三個棱所作的三個矢量，常 用用 表示。表示。cba,：指晶胞的邊長：指晶胞的邊長固體物理學原胞固體物理學原胞:最小重復單元最小重復單元只反映周期性只反映周期性 ()晶體學原胞晶體學原胞:反映反映周期性周期性和和對稱性對稱性 （) 非晶體非晶體中，質點雖然可以是近程有序的中，質點雖然可以是近程有序的(每一黑點為每一黑點為三個圓圈圍繞三個圓圈圍繞)，但不存在長程有序！，但不存在長程有序！非晶體非晶體液體和非晶體中的液體和非晶體中的短程序短程序：1.參考原子第一配位殼層的結構參考原子第一配位殼層的結構有序化，其范圍為有序化，其范圍

11、為0.35 0.4nm以內；以內；2.基于徑向分布函數上可以清晰基于徑向分布函數上可以清晰的分辨出第一峰與第二峰，有明的分辨出第一峰與第二峰，有明確的最近鄰和次近鄰配位層，其確的最近鄰和次近鄰配位層，其范圍一般為范圍一般為0.3 0.5nm學習內容學習內容：定義定義一、一、簡單立方晶格（簡單立方晶格（SC格子）格子） 二、面心立方晶格二、面心立方晶格 三、體心立方晶格三、體心立方晶格 四、六角密排晶格四、六角密排晶格 五、金剛石晶體結構五、金剛石晶體結構 六、氯化鈉結構六、氯化鈉結構七、氯化銫晶格七、氯化銫晶格了解幾個定義了解幾個定義：1 配位數配位數：原子的最近鄰（原子）數目：原子的最近鄰（

12、原子）數目2 致密度致密度：晶胞中原子所占體積與晶胞體積之比：晶胞中原子所占體積與晶胞體積之比注：配位數和致密度注：配位數和致密度 原子堆積成晶格時愈緊密原子堆積成晶格時愈緊密3 密排面密排面：原子球在一個平面內最緊密排列的方式：原子球在一個平面內最緊密排列的方式把密排面疊起來可以形成原子球最緊密堆積的晶格。把密排面疊起來可以形成原子球最緊密堆積的晶格。一、簡單立方晶格（一、簡單立方晶格（SCSC格子）格子）1 配位數配位數：每個原子的上下左右前后各有一個最近鄰：每個原子的上下左右前后各有一個最近鄰 原子原子 配位數為配位數為6 2 堆積方式堆積方式：最簡單的原子球規則排列形式：最簡單的原子球

13、規則排列形式 沒有沒有 實際的晶體具有此種結構實際的晶體具有此種結構 簡單立方晶簡單立方晶 格堆積方式格堆積方式簡單立方晶簡單立方晶格典型單元格典型單元4 晶格的三個基矢晶格的三個基矢：kaajaaiaa321a 為晶格常數為晶格常數3 原胞原胞： SC格子的立方單元是最小的周期性單元格子的立方單元是最小的周期性單元 選取其本身為原胞選取其本身為原胞簡單立方簡單立方晶格原胞晶格原胞1a2a3a二、面心立方晶格（二、面心立方晶格（face-centered cubic fcc）1 配位數配位數：每個原子在：每個原子在 上、下平面位置對角線上上、下平面位置對角線上 各有四個最近鄰原子各有四個最近鄰

14、原子 配位數為配位數為122 堆積方式堆積方式：ABC ABC ABC,是一種最緊是一種最緊 密密 的排列方式，常稱為立方密排晶格的排列方式，常稱為立方密排晶格3 原胞原胞: 由一個由一個立方體頂點立方體頂點到到三個近鄰的面心三個近鄰的面心引晶格引晶格 基矢，得到以這三個晶格基矢為邊的原胞基矢，得到以這三個晶格基矢為邊的原胞4 晶格的三個基矢晶格的三個基矢：ikaakjaajiaa2223215 原胞的體積原胞的體積：fccaaaa4143321原胞原胞fccaaaa4143321原胞原胞 fcc 格子的一個立方單元體積中含的原子數：格子的一個立方單元體積中含的原子數：4又又fccaaaa41

15、43321原胞原胞原胞中只包含一個原子原胞中只包含一個原子 因而為最小周期性單元因而為最小周期性單元注注： fcc 晶格方式是一種最緊密的排列方式晶格方式是一種最緊密的排列方式 立方密排晶格！立方密排晶格！fccaaaa4143321原胞原胞6 判斷此原胞為判斷此原胞為fcc格子的最小周期性單元格子的最小周期性單元面心立方晶格的堆積方式面心立方晶格的堆積方式面心立方晶格的典型單元和原子密排面面心立方晶格的典型單元和原子密排面1a2a3a面心立方晶格的原胞面心立方晶格的原胞1 配位數配位數:每個原子都可作為體心原子，分布在八個每個原子都可作為體心原子，分布在八個 結點上的原子都是其最近鄰結點上的

16、原子都是其最近鄰 原子原子 ,CN=82 堆積方式堆積方式：正方排列原子層之間的堆積方式表示正方排列原子層之間的堆積方式表示 為為 AB AB AB 原子球不是緊密靠原子球不是緊密靠 在一起在一起3 原胞原胞：由一個立方體由一個立方體頂點頂點到最近的到最近的三個體心三個體心得到晶得到晶 格基矢格基矢,以它們為棱形成的平行六面體構成以它們為棱形成的平行六面體構成 原胞原胞4 晶格的三個基矢晶格的三個基矢：kjiaakjiaakjiaa2223215. 原胞的體積原胞的體積：bccaaaaV2123321原胞原胞bccaaaa2123321原胞原胞bcc 的一個立方單元體積中，包含兩個原子的一個立

17、方單元體積中，包含兩個原子,此原胞中只含有一個原子此原胞中只含有一個原子 其為最小周期性單元其為最小周期性單元!bccaaaa2123321原胞原胞bccaaaaV2123321原胞原胞體心立方晶格的堆積方式體心立方晶格的堆積方式體心立方晶格的典型單元體心立方晶格的典型單元體心立方晶格的原胞體心立方晶格的原胞1a2a3a1 配位數配位數 ：理想情況：理想情況 所有相鄰原子之間的距離相所有相鄰原子之間的距離相 等等 軸比軸比 配位數配位數為為12 實際值在實際值在1.571.64之間波動之間波動 633.13/8/ac2 堆積方式堆積方式：AB AB AB，上、下兩個底面為，上、下兩個底面為A

18、層，中間的三個原子為層，中間的三個原子為 B 層層3 原胞原胞： 在密排面內，互成在密排面內，互成1201200 0角，角， 沿垂直沿垂直 密排面的方向構成的菱形柱體密排面的方向構成的菱形柱體 原胞原胞21,aa3a六角密排晶格的堆積方式六角密排晶格的堆積方式六角密排晶格結構的典型單元六角密排晶格結構的典型單元ABca六角密排晶格結構的原胞六角密排晶格結構的原胞1a2a3aA A層內原子的上、下各層內原子的上、下各3 3個最個最近鄰原子所分別形成的正三近鄰原子所分別形成的正三角形的空間取向，不同于角形的空間取向，不同于B B面內原子的上、下各面內原子的上、下各3 3個最個最近鄰原子所分別形成的

19、正三近鄰原子所分別形成的正三角形的空間取向！角形的空間取向！4 注意注意: A 層中的原子層中的原子 B 層中的原子層中的原子 復式晶格復式晶格A 層層B 層層由分別位于由分別位于A A層與層與B B層的簡單六角格子層的簡單六角格子沿沿OOOO方向穿套而成！方向穿套而成！六角密排晶格結構的典型單元六角密排晶格結構的典型單元ABca五、金剛石晶體結構五、金剛石晶體結構1 特點特點：每個原子有每個原子有4 個最近鄰，它們正個最近鄰，它們正 好在一個正四面體的頂角位置好在一個正四面體的頂角位置2 堆積方式堆積方式：立方單元體內對角線上的原子立方單元體內對角線上的原子 A 面心立方位置上的原子面心立方

20、位置上的原子 B3 注意注意：復式晶格的原胞復式晶格的原胞 = = 相應的簡單晶格的原胞相應的簡單晶格的原胞 原胞中包含每種等價原子各一個原胞中包含每種等價原子各一個4 原胞原胞：B B 原子組成的面心立方原胞原子組成的面心立方原胞 + + 一個一個A A原子原子金剛石晶格的原胞金剛石晶格的原胞六、氯化鈉六、氯化鈉(NaCl)(NaCl)結構結構1 特點特點：NaCl 結構的布拉伐格子是結構的布拉伐格子是 fcc 格子格子 基元基元 = Na+ + Cl- (相距半個晶格常數相距半個晶格常數)2 堆積方式堆積方式: Na+ 和和 Cl-本身構成面心立方晶格本身構成面心立方晶格 NaCl晶格晶格

21、 Na+ 和和 Cl- 的面心立方晶格穿套而成的面心立方晶格穿套而成3 原胞原胞：Na+ 的面心立方原胞中心的面心立方原胞中心 + 一個一個Cl-NaCl晶格的原胞晶格的原胞NaCl晶格結構的典型單元晶格結構的典型單元七、氯化銫（七、氯化銫（CsCl)CsCl)晶格晶格1 特點特點：布拉伐格子是布拉伐格子是 SC 格子格子 Cs+ + Cl- 分別形成分別形成 的的SC格子套構而成的復式晶格格子套構而成的復式晶格2 原胞原胞：Cl- 的簡單立方原胞中心的簡單立方原胞中心 + 一個一個 Cs+ Cl-CsCl晶格的原胞晶格的原胞CsCl晶格的典型單元晶格的典型單元Cs+1.它是體積最小的重復單元

22、它是體積最小的重復單元,具有具有Bravais格子的全部格子的全部 宏觀對稱性宏觀對稱性2.每個原胞只包含一個格點每個原胞只包含一個格點 魏格納魏格納 - 塞茲原胞塞茲原胞的的格點位于原胞中央；格點位于原胞中央； 平行六面體形原胞平行六面體形原胞的的8個格點位于平行六面體的個格點位于平行六面體的8個個 頂角，每個格點為頂角，每個格點為8個原胞所共有個原胞所共有 每個原胞平每個原胞平 均包含一個格點！均包含一個格點！二維晶格的二維晶格的Wigner-Seitz原胞原胞取法：取法：作某格點與所有其他格點連線的中垂面，被這些中作某格點與所有其他格點連線的中垂面，被這些中垂面圍在中央的最小多面體垂面圍

23、在中央的最小多面體 Wigner-Seitz原胞原胞332211alalal321ll l321ll l100110111111:111:111 l :k :h 332211332211332211yxyxyxzxzxzxzyzyzymnp222)(lkhadhkl222)(2lkhadhkl222)(lkhadhkl111金剛石晶格中金剛石晶格中雙層密排面雙層密排面111rk倒易點陣是傅立葉空間中的點陣倒易點陣是傅立葉空間中的點陣;倒易點陣的陣點告訴我們一個具有晶體點陣周期性倒易點陣的陣點告訴我們一個具有晶體點陣周期性的函數傅立葉級數中的波矢在波矢空間的分布情況，的函數傅立葉級數中的波矢在波

24、矢空間的分布情況，倒易點陣陣點分布決定于晶體點陣的周期性質倒易點陣陣點分布決定于晶體點陣的周期性質; ;一個給定的晶體點陣，其倒易點陣是一定的一個給定的晶體點陣，其倒易點陣是一定的，因此，因此，一種晶體結構有兩種類型的點陣與之對應：晶體點一種晶體結構有兩種類型的點陣與之對應：晶體點陣是陣是真實空間真實空間中的點陣，量綱為中的點陣，量綱為LL；倒易點陣是；倒易點陣是傅傅立葉空間立葉空間中的點陣中的點陣, ,量綱為量綱為L-1L-1。如果把晶體點陣本身理解為如果把晶體點陣本身理解為周期函數周期函數，則倒易點陣就是晶體點陣的，則倒易點陣就是晶體點陣的傅立葉變換傅立葉變換，所以倒易點陣也是晶體結構周期

25、性的所以倒易點陣也是晶體結構周期性的數學抽象數學抽象，只是在不同空間，只是在不同空間( (波矢波矢空間空間) )來反映來反映, ,其所以要變換到波矢空間是由于其所以要變換到波矢空間是由于研究周期性結構中波動過程的需要。研究周期性結構中波動過程的需要。一個三維周期性函數一個三維周期性函數u(r)（周期為（周期為T=n1a1+ n2a2+ n3a3） 即：即：u(r) = u(r + T)r是實數自變量，可以用來表示三維實空間的坐標。是實數自變量，可以用來表示三維實空間的坐標。那么如果將那么如果將u(r)展開成傅立葉級數，其形式為：展開成傅立葉級數，其形式為： u(r) = G uG exp(iG

26、r)G是與實空間中的周期性矢量是與實空間中的周期性矢量T相關聯的一組矢量相關聯的一組矢量 321a ,a ,a332211la a aRlll213212131332113232321321222222aaaaaaabaaaaaaabaaaaaaab213212131332113232321321222222aaaaaaabaaaaaaabaaaaaaab213212131332113232321321222222aaaaaaabaaaaaaabaaaaaaab321aaa321,bbb332211321bhbhbhGhhh321,hhh321hhhG3 , 2 , 1, 0,22jijiji

27、baijji332211la a aRlllrkie.選擇適當的波矢選擇適當的波矢 使平面波具有給定布拉伐格子使平面波具有給定布拉伐格子 的的周期性周期性k具有給定具有給定布拉伐格子周期性布拉伐格子周期性的那些的那些平面波波矢平面波波矢 所所代表的點的集合代表的點的集合 稱為稱為倒格子倒格子hGkrGirRGihlhee.rlRrGirRGihlhee.hG1.lhRGielhlhlhrGirGiRGieee.332211bhbhbhGh321,bbb321,hhh22.332211332211332211hlhlh lalala lbhbhbhRGlh22.33221133221133221

28、1hlhlhlalalalbhbhbhRGlh22.332211332211332211hlhlhlalalalbhbhbhRGlh12sin2cos.sin.cos.iRGiRGehhRGilh12sin2cos.sin.cos.iRGiRGehhRGilh12sin2cos.sin.cos.iRGiRGehhRGilh3 , 2 , 1, 0,22jijijibaijji1.lhRGie213212131332113232321321222222aaaaaaabaaaaaaabaaaaaaab213212131332113232321321222222aaaaaaabaaaaaaabaaa

29、aaaab213212131332113232321321222222aaaaaaabaaaaaaabaaaaaaab313233211312133233211332321222222aaaaaaaaaaaaaaaaaaabbb 313233211312133233211332321222222aaaaaaaaaaaaaaaaaaabbb313233211312133233211332321222222aaaaaaaaaaaaaaaaaaabbb313233211312133233211332321222222aaaaaaaaaaaaaaaaaaabbb31323321131213323321

30、1332321222222aaaaaaaaaaaaaaaaaaabbb321hhhG3212hhhd321hhhG321hhhG0.0.21321321lGlGhhhhhh321hhhGn1a3a2a倒格式倒格式 和晶面和晶面 (h1 h2 h3)的關系的關系321hhhG321,aaa332211,haOChaOBhaOA1122hahaOAOBAB0221122332211321hahabhbhbhABGhhhjijibaijji, 0,22321hhhG321hhhG321hhhG3213212hhhhhhdG321hhhd321321321/hhhhhhhhhGGn3213213213

31、213213213212233221111hhhhhhhhhhhhhhhhhhhhhGdGGbhbhbhhanOAdnAO又3213213213213213213212233221111hhhhhhhhhhhhhhhhhhhhhGdGGbhbhbhhanOAdnOA又3213212hhhhhhGd321hhhGn1a2a3a1 Brillouin Zone 的定義和確定方法的定義和確定方法 對于給定的晶格對于給定的晶格321,aaa321,bbb正格子基矢正格子基矢 倒格子基矢倒格子基矢 332211321bhbhbhGhhh由由 確定確定該晶格的倒格子該晶格的倒格子被上述平面所包圍的圍繞被上

32、述平面所包圍的圍繞原點原點的最小區域稱為第一的最小區域稱為第一布里淵區，也稱為布里淵區，也稱為簡約布里淵區簡約布里淵區 以任一倒格點為原點，作所有倒格矢以任一倒格點為原點，作所有倒格矢 的垂直的垂直 平分面平分面 這些平面將倒格子空間分割為許多區域這些平面將倒格子空間分割為許多區域nG SC 的倒格子仍為的倒格子仍為簡單立方結構簡單立方結構； bcc 格子的倒格子具有格子的倒格子具有 fcc 結構結構 ； fcc 格子的倒格子具有格子的倒格子具有 bcc 結構結構; 即即 bcc 與與 fcc 互為正倒格子互為正倒格子 !32ikaakjaajiaa2223212132121313321132

33、32321321222222aaaaaaabaaaaaaabaaaaaaab213212131332113232321321222222aaaaaaabaaaaaaabaaaaaaab213212131332113232321321222222aaaaaaabaaaaaaabaaaaaaabkjiabkjiabkjiab222321ikabkjabjiab222321kjiabkjiabkjiab222321iaaiab2O一維晶格點陣一維晶格點陣aOb倒格子點陣倒格子點陣-/a/ajiaaaa21和jabiab2221和NoImageM(x1, x2, x3)M(x1, x2, x3)剛性圖

34、形的轉動剛性圖形的轉動1. 基本對稱操作基本對稱操作體系中一點體系中一點M 的位矢為的位矢為x xMxRM321333231232221131211321xxxRRRRRRRRRxxx操作操作實際就是實際就是晶體坐標晶體坐標(格點坐標格點坐標)的某種變換。因為操作應不改變晶體中的某種變換。因為操作應不改變晶體中任意兩點間的距離，所以用數學表示，這些操作就是任意兩點間的距離，所以用數學表示，這些操作就是線性變換線性變換。xcossinsincoscossinsinsincossinsincoscoscos32332211xxxxxxxxxxxxxxcossincossinsincossinsincossinsincoscoscos32332211xxxxxxxxxxxxxxcossinsincoscossinsinsincossinsincoscoscos32332211xxxxxxxxxxxxxx321321cossin0sinc