生物統計學

（BiologyStatistic）統計遺傳教研室分子生物學館106張明明本課內容的主要安排：（1）擬合優度檢驗（2）回歸分析（一元、多元、logistic）（3）方差分析（4）試驗設計第一章生物統計學概述

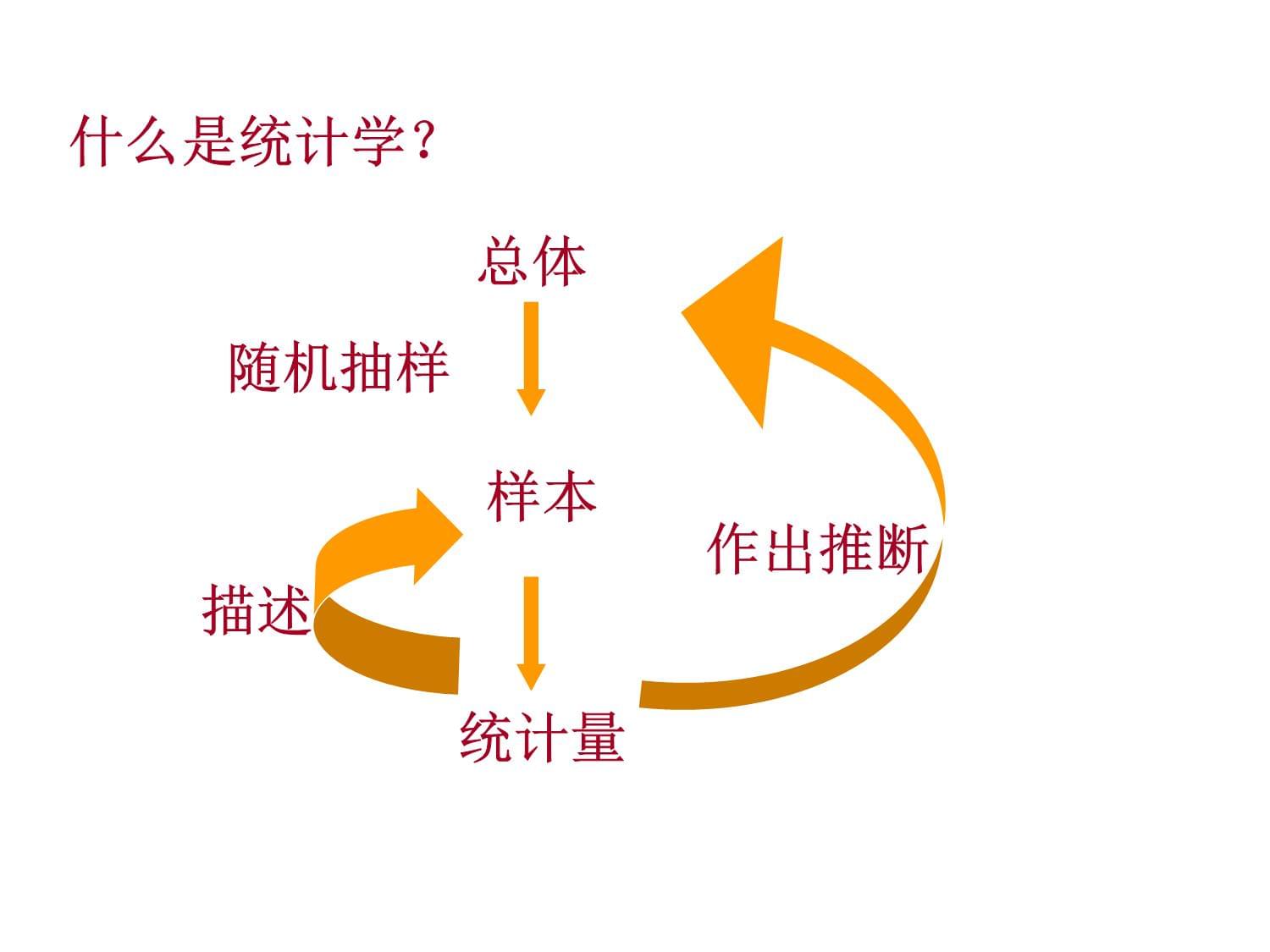
總體樣本統計量描述作出推斷隨機抽樣什么是統計學？1.生物統計學概念生物統計學是以概率理論為基礎，研究生命科學中隨機現象規律性的應用數學科學。2.應用領域

林學、農學、醫藥學等等。3.研究內容

用統計方法研究生物問題。4.常用軟件

SAS、SPSS、Excel、Statistic第一節、中心趨勢指標常用的中心趨勢指標有：算術均數、幾何均數、中位數、眾數，統稱為平均數（average）一、算術平均數（TheArithmeticmean）簡稱均數（Mean）或均值，定義為所有測量值之和除以變量值個數（即，樣本含量SampleSize）。反映一組呈對稱分布的變量值在數量上的平均水平。（1）直接計算法

公式：舉例1：試計算1，3，7，9的均數？例2：試計算1，3，3，7，7，9，9，9的均數？（2）加權法

均數的特征二、

中位數與百分位數11個大鼠存活天數：4，10，7，50，3，15，2，9，13，>60，>60平均存活天數?（一）中位數（median）是將每個變量值從小到大排列，位置居于中間的那個變量值。

存活天數2，

3，

4，7，9，10，13，15，50，>60，>60秩次1234567891011計算公式:

n為奇數時

n為偶數時

例

9名中學生甲型肝炎的潛伏期分別為12，13，14，14，15，15，15，17,天，求其中位數。19頻數表資料的中位數下限值L上限值Ui;fm中位數M中位數＝4.5+0.5x[(150x50%－68)/37]＝4.59中位數的特征計算時只利用了位置居中的測量值優點：對極值不敏感缺點：并非考慮到每個觀測值適用于各種分布類型的資料，特別適合于：大樣本偏態分布資料或者一端或兩端無確切數值的資料

百分位數示意圖（二）百分位數（percentile）1．直接計算法

設有n個原始數據從小到大排列，第X百分位數的計算公式為：當為帶有小數位時：

當為整數時：Trunc()取整函數

例

對某醫院細菌性痢疾治愈者的住院天數統計，120名患者的住院天數從小到大排列如下，試求第5百分位數和第99百分位數。患者：住院天數：

（1）n=120，

，為整數：

（2），帶有小數，故取整trunc（118.8）=118患者：住院天數：2．頻數表法

公式：

例

試分別求表1.3頻數表的第25、第75百分位數。P25＝4.0+0.5x[(150x25%－36)/32]=4.02P75＝5.0+0.5x[(150x75%－105)/22]=5.17三、幾何均數（geometricmean）

可用于反映一組經對數轉換后呈對稱分布或正態分布的變量值在數量上的平均水平。(1)直接法幾何均數：變量對數值的算術均數的反對數。

其他對數（如自然對數）變換獲得相同的幾何均數例6測定10名傷寒病人血清抗體滴度分別為1：4，1：4，1：4，1：4，1：4，1：16，1：16，1：16，1：64，1：128，求其平均抗體滴度。以其滴度的倒數為原變量值，代入公式有：平均抗體滴度為：1：11（2）加權法公式：例6的血清抗體滴度資料的頻數表1、幾何均數適用于對數正態分布，如藥物的效價、抗體的滴度、傳染性疾病的潛伏期等資料。2、變量x服從對數正態分布，即表示變量lg(xi)服從正態分布。對于lg(xi)，具有正態分布的所有特性。幾何均數的特征四、眾數（Mode）是一群數據中出現次數（頻數）最多的值。適用于大樣本；較粗糙。例

有16例高血壓病人的發病年齡(歲)為：42,45,48,51,52,54,55,55,,61,61,62,62，試求眾數。眾數的特征1、對于某些數據而言，例如均勻分布，并不存在眾數；2、對于某些數據存在兩個或多于兩個的眾數；3、定性數據可以存在眾數；眾數對于進一步的統計學計算與分析不具備應用價值。58,58,58,58五、其他位置指標1、四分位數（Quartile）（三個四分位數）2、十分位數(Centile):9個十分位數3、百分位數（Percentile）99個百分位數離散與變異性指標全距四分位間距方差標準差變異系數

一、全距(Range)與絕對差全距為最大值與最小值之差，也叫極差缺點：僅利用了兩個極端值。二、方差與標準差方差(Variance)也稱均方差（meansquaredeviation），反映一組數據的平均離散水平。(一)樣本方差為各變量值到樣本均數距離的平方和除以自由度的商值，即(二）總體方差定義為樣本標準差為樣本方差的平方根；

總體標準差為總體方差的平方根。標準差（standarddeviation）樣本標準差實用公式樣本標準差的加權公式隨機變量xi的標準化如果隨機變量xi服從正態分布，均數和標準差分別為和s，則隨機變量xi的標準化正態離差值（Standardnormaldeviation）又稱為標準化得分值（StandardScores）為：三、變異系數

（coefficientofvariation）

變異系數(coefficientofvariation，CV)常用于比較度量單位不同或均數相差懸殊的兩組(或多組)資料的變異程度。

某地7歲男孩身高的均數為123.10cm，標準差為4.71；體重均數為22.59kg，標準差為2.26kg,

比較其變異度？

四、四分位數間距

（inter-quartilerange）

四分位數間距，用IQR表示：

IQR=第三四分位數：Q3

第一四分位數：Q1第三節率、比及其注意事項一、率（rate）：在特定條件下,可能發生某現象的總例數中，實際發生某現象的強度或頻率。構成比（Proportion，constituentratio）：構成比指標用以表示事物內部某一構成成分在全部構成中所占的比例或比重。相對比（relativeratio）是由兩個有關聯的指標之比。二、比（ratio）第四節常用統計圖介紹1.條圖：單式條圖和復式條圖2.圓圖（餅圖）3.百分條圖4.線圖5.直方圖6.概率—概率散點圖（P—P概率圖）7.莖葉圖8.盒式圖地區北非及中東西歐北美洲拉丁美洲南亞及東南亞成人感染率/%0.130.250.560.570.69復式條圖例：19941998受檢人數異常人數檢出率%受檢人數異常人數檢出率%血壓519558.89582386.52心率519448.48582396.70（2）圓圖（餅圖）用圓的總面積表示事物的全部，各個扇形的面積（圓心角的大小）表示各個部分的比重，適用于百分比資料。類別老年青年中年小孩比例/%33％15％45％7％（3）百分條圖百分條圖是用一個矩形的面積表示事物的全部，而用其中各段表示個構成部分。例：（4）線圖（i）簡單線圖：一條折線或一條曲線（ii）多重線圖：多條折線折線圖年份結核病死亡率白喉死亡率1947150.220.11950148.016.61951141.014.01952130.011.81953110.410.7195498.26.5195572.63.9195668.02.4195754.81.3（5）直方圖直方圖以各矩形的面積表示各組段的頻數，各矩形面積的總和為總頻數，用于表示連續性資料的頻數分布。（6）概率——概率散點圖（P-P概率圖）是以橫軸表示一個變量的經驗累積分布函