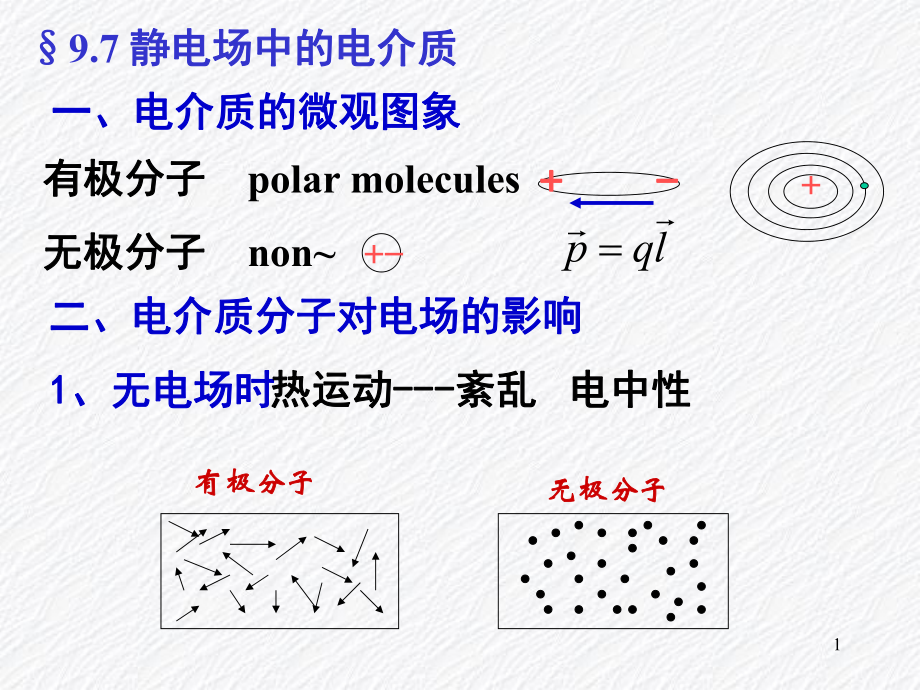
1、1一、電介質的微觀圖象一、電介質的微觀圖象+ -+ -+-+有極分子有極分子 polar molecules無極分子無極分子 nonl qp二、電介質分子對電場的影響二、電介質分子對電場的影響1 1、無電場時、無電場時有極分子有極分子無極分子無極分子電中性電中性熱運動熱運動-紊亂紊亂9.7 靜電場中的電介質靜電場中的電介質22. 有電場時有電場時 電介質分子的極化電介質分子的極化結論：結論：極化的極化的總總效果是介質邊緣效果是介質邊緣出現出現電荷分布電荷分布稱呼：稱呼：由于這些電荷仍由于這些電荷仍束縛在每個分子中束縛在每個分子中 所以所以稱之為稱之為束縛電荷束縛電荷或或極化電荷極化電荷 有極分

2、子介質有極分子介質位移極化位移極化 無極分子介質無極分子介質取向極化取向極化 均勻均勻E均勻均勻E 3電偶極子排列的有序程度電偶極子排列的有序程度反映了介質被極化的程度反映了介質被極化的程度排列愈有序說明極化愈烈排列愈有序說明極化愈烈3.描述極化強弱的物理量描述極化強弱的物理量-極化強度極化強度 V宏觀上無限小宏觀上無限小微觀上無限大微觀上無限大的體積元的體積元VSI2mC單位單位ip每個分子的每個分子的電偶極矩電偶極矩VpPiiV0lim定義定義4三、極化強度與極化電荷的關系三、極化強度與極化電荷的關系在已極化的介質內任意作一閉合面在已極化的介質內任意作一閉合面S基本認識基本認識：1）S 把

3、位于把位于S 附近的電介質分子分為附近的電介質分子分為兩部分兩部分 一部分在一部分在 S 內內 一部分在一部分在 S 外外2）只有只有電偶極矩電偶極矩穿過穿過S 的分子對的分子對S內外內外的極的極化電荷化電荷才才有有貢獻貢獻S5SdcosSqnlqddcosSPdSPd1.小面元小面元dS附近分子對面附近分子對面S S內極化電荷的貢獻內極化電荷的貢獻S 分子數密度為分子數密度為 nlP外場外場Sd在在dS附近薄層內認為介質均勻極化附近薄層內認為介質均勻極化薄層：以薄層：以dS為底、長為為底、長為l的圓柱的圓柱只有中心落在薄層內的分子才只有中心落在薄層內的分子才對面對面S內電荷有貢獻內電荷有貢獻

4、所以，所以，lnqP6SP- SPqnddd面面內極化電荷的正負取決于內極化電荷的正負取決于 ；將電荷的正負考慮進去，得小面將電荷的正負考慮進去，得小面元元dS附近分子對面附近分子對面內內極化電荷的極化電荷的貢獻寫成貢獻寫成2.在在S所圍的體積所圍的體積內內的極化電荷的極化電荷與與的關系的關系qPSSPqdPSd ldSV面內面內問題：問題：面元的法面元的法線方向是線方向是如何規定如何規定的？的？7Sqdd nP介質外法線方向介質外法線方向PdSSd l內內n P3.電介質表面（電介質表面（外外）極化電荷面密度）極化電荷面密度sPn sPsPqndddd面外面外n n P8四、四、電介質的極化

5、規律電介質的極化規律1.各向同性線性電介質各向同性線性電介質 isotropy linearity介質的電極化率介質的電極化率EPe01re無量綱的純數無量綱的純數eE與與無關無關2.各向異性線性電介質各向異性線性電介質 anisotropy 張量描述張量描述eE與與、與晶軸的方位有關、與晶軸的方位有關9五、五、自由電荷與極化電荷共同產生場自由電荷與極化電荷共同產生場例例1 介質細棒的一端放置一點電荷介質細棒的一端放置一點電荷EEE00Q1q2qPP點的場強？點的場強？EE0自由電荷產生的場自由電荷產生的場束縛電荷產生的場束縛電荷產生的場介質棒被極化，產生極化電荷介質棒被極化，產生極化電荷q1

6、 q2 。極化電荷極化電荷q1 q2和自由電荷和自由電荷Q0共同產生場共同產生場10求求: :板內的場強板內的場強解解: :均勻極化均勻極化 表面出現束縛電荷表面出現束縛電荷內部的場由內部的場由自由電荷自由電荷和和 束縛電荷束縛電荷 共同產生共同產生例例2 平行板電容器平行板電容器 , ,自由電荷面密度為自由電荷面密度為0 000r其間充滿相對介電常數為其間充滿相對介電常數為 r的均勻的各向的均勻的各向同性的線性電介質同性的線性電介質0在真空中疊加在真空中疊加11EEE0rE00rEE0介介質質0該式普該式普遍適用遍適用嗎？嗎？000E0E0EE)1 (00o)2()1(0EPrn得得00單獨

7、產生的場強為單獨產生的場強為單獨產生的場強為單獨產生的場強為12均勻各向同性電介質充滿均勻各向同性電介質充滿兩個等勢面之間兩個等勢面之間rEE0例例3 導體球導體球Q置于均勻各向同性介質中置于均勻各向同性介質中 如圖示如圖示求：場的分布求：場的分布00R1R2R1r2r13解：解：01E0P0P21024rQEr21010241rQPrr22034rQEr22020341rQPrr2044rQE00R1R2R1r2r0Rr 10RrR21RrR2Rr 導體內部導體內部1r內內2r內內真空真空14各向同性線性電介質均勻充滿兩個等勢面間各向同性線性電介質均勻充滿兩個等勢面間思路思路qnPEPEEE

8、rr1000六、電位移矢量六、電位移矢量 1、定義、定義DEP0量綱量綱 PD單位單位 C/m2各向同性線性介質各向同性線性介質EPr) 1(0DEr 0介質方程介質方程無直接物理含義無直接物理含義iiSqSD0d2、有介質時的、有介質時的高斯定理高斯定理表達式：表達式：SiiqSE0dqqioiii0證：證：靜電場中電位移矢量的通量等于閉合面內包靜電場中電位移矢量的通量等于閉合面內包圍的自由電荷的代數和圍的自由電荷的代數和自由電荷代數和自由電荷代數和iiiiqq0面內束縛電荷之代數和面內束縛電荷之代數和面內自由電荷之代數和面內自由電荷之代數和ioiSSqSPSEdd0iiSqSD0diiqS

9、PE00Sd證畢證畢SiiiiqqSE00diiSqSD0d1）有介質時靜電場的性質方程有介質時靜電場的性質方程2）在解場方面的應用在解場方面的應用 在具有某種對稱性的情況下在具有某種對稱性的情況下 可以首先由高斯定理解出可以首先由高斯定理解出DDEPq 思路思路討論討論19七、有電介質時電場、束縛電荷的計算七、有電介質時電場、束縛電荷的計算 SqSdD0EDPE ,P0qDnP EPEDrr100 20【例【例】一帶正電的金屬球浸在油中。求球外的電一帶正電的金屬球浸在油中。求球外的電場分布和貼近金屬球表面的油面上的束縛電荷。場分布和貼近金屬球表面的油面上的束縛電荷。R+-qqr qrD 24

10、 2004rqDErr2002044rqErqEr 24 rqDD 的高斯定理的高斯定理PEDr為什么？為什么？解：解：21220004)11 (4) 1() 1(rqrqEPrrrrR+-qqPEDrqRqr)11(42 總 與總 與 反 號 ， 數 值 小 于反 號 ， 數 值 小 于 。q qq24)11 (RqPr球表面的油面上的束縛電荷：球表面的油面上的束縛電荷：-rP(R)220 E另一解法：另一解法：ErPr) 1() (0 用用 E 的高斯定理的高斯定理qqrr)11()11( R+-qqr + +- S23例：已知：平行板電容器例：已知：平行板電容器V300 , 00U充一半電介質：充一半電介質：5r求：求：UEDED , , , , , , 202211011解：解：介質分界面介質分界面 等勢面，等勢面， 未破壞各部分的面對稱性，未破壞各部分的面對稱性， 選底面與帶電平板平行的選底面與帶電平板平行的 圓柱面為高斯面。圓柱面為高斯面。2010102011r dnPS242010側上下SDSDSDSDSDs11111dddd導體內導體內0E0cosSqS(10)0內由高斯定理由高斯定理)(01d內SsqSDSSD101rDED011101 2010102011r dnPS2502220