1、精選優質文檔-傾情為你奉上 1. 平面上一點向二次曲線作切線得兩切點，連結兩切點的線段我們稱切點弦.設過拋物線外一點的任一直線與拋物線的兩個交點為C、D，與拋物線切點弦AB的交點為Q。（1）求證：拋物線切點弦的方程為；（2）求證：.2. 已知定點F（1，0），動點P在y軸上運動，過點P作PM交x軸于點M，并延長MP到點N，且（1）動點N的軌跡方程；（2）線l與動點N的軌跡交于A，B兩點，若，求直線l的斜率k的取值范圍.3. 如圖，橢圓的左右頂點分別為A、B，P為雙曲線右支上（軸上方）一點，連AP交C1于C，連PB并延長交C1于D，且ACD與PCD的面積相等，求直線PD的斜率及直線CD的傾斜角.

2、4. 已知點，動點滿足條件.記動點的軌跡為.（）求的方程；（）若是上的不同兩點，是坐標原點，求的最小值.5. 已知曲線C的方程為:kx2+(4-k)y2=k+1,(kR) （）若曲線C是橢圓，求k的取值范圍；（）若曲線C是雙曲線，且有一條漸近線的傾斜角是60°，求此雙曲線的方程；（）滿足（）的雙曲線上是否存在兩點P，Q關于直線l：y=x-1對稱，若存在，求出過P，Q的直線方程；若不存在，說明理由。6. 如圖（21）圖，M（-2，0）和N（2，0）是平面上的兩點，動點P滿足：(1)求點P的軌跡方程；(2)若,求點P的坐標.7. 已知為橢圓的右焦點，直線過點且與雙曲線的兩條漸進線分別交于

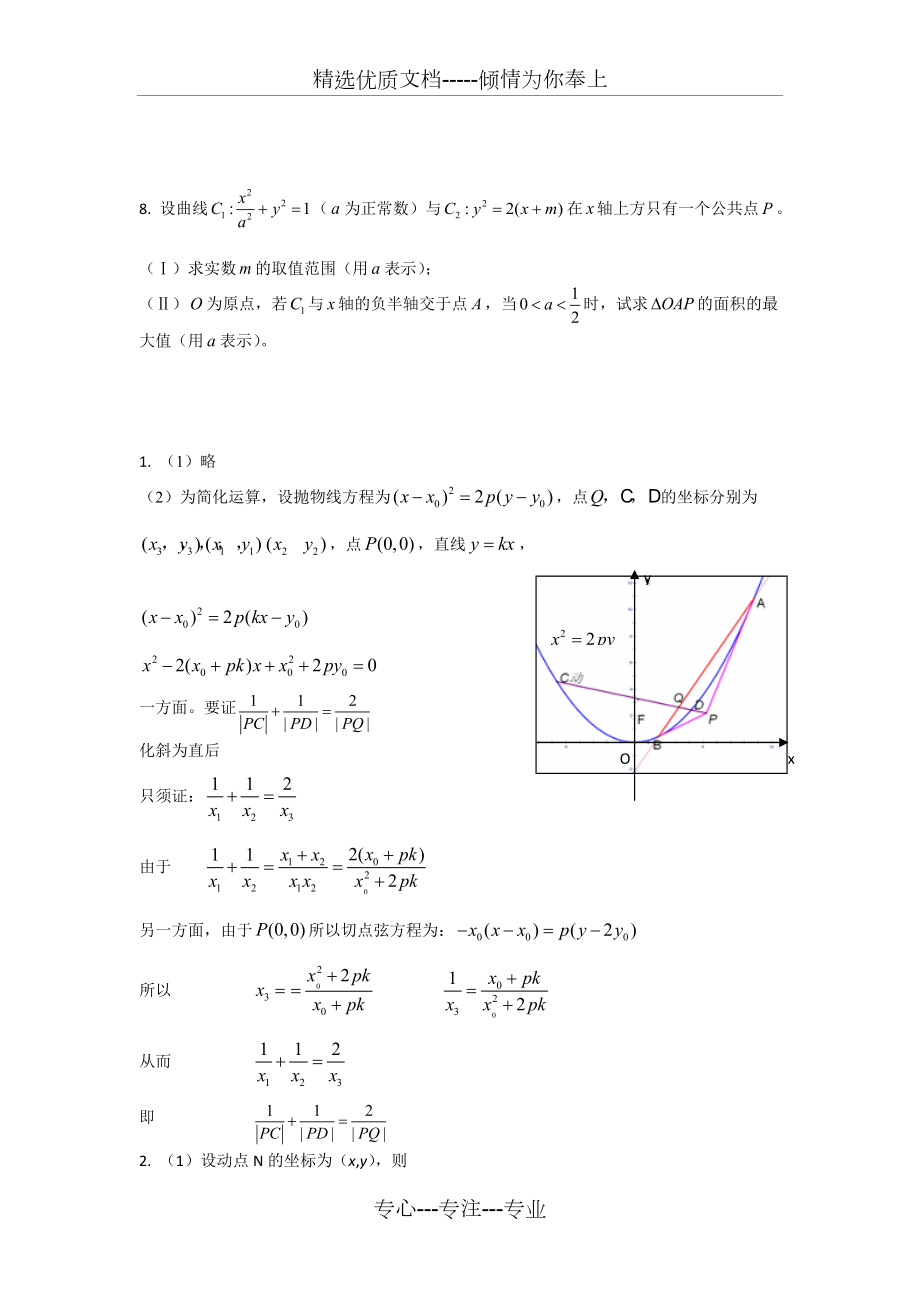
3、點，與橢圓交于點.（I）若，雙曲線的焦距為4。求橢圓方程。（II）若（為坐標原點），求橢圓的離心率。8. 設曲線（為正常數）與在軸上方只有一個公共點。（）求實數的取值范圍（用表示）；（）為原點，若與軸的負半軸交于點，當時，試求的面積的最大值（用表示）。1. （1）略xyO（2）為簡化運算，設拋物線方程為，點的坐標分別為，點，直線，一方面。要證化斜為直后只須證：由于另一方面，由于所以切點弦方程為：所以從而即2. （1）設動點N的坐標為（x,y），則 2分，因此，動點的軌跡方程為 4分（2）設l與拋物線交于點A（x1,y1）,B(x2,y2)，當l與x軸垂直時，則由， 不合題意，故與l與x軸不垂直

4、，可設直線l的方程為y=kx+b(k0),則由6分由點A，B在拋物線又y2=4x, y=kx+b得ky24y+4b=0,8分所以10分因為解得直線l的斜率的取值范圍是.12分3. 由題意得C為AP中點，設，把C點代入橢圓方程、P點代入雙曲線方程可得解之得：故直線PD的斜率為，直線PD的方程為聯立，故直線CD的傾斜角為90°4. 解法一： （）由|PM|PN|=知動點 P 的軌跡是以 為焦點的雙曲線的右支，實 半軸長又半焦距 c=2，故虛半軸長所以 W 的方程為, （）設 A，B 的坐標分別為, 當 ABx軸時,從而從而當AB與x軸不垂直時,設直線AB的方程為,與W的方程聯立,消去y得

5、故 所以 .又因為,所以,從而綜上,當AB軸時, 取得最小值2.解法二:(）同解法一. （）設 A，B 的坐標分別為，則, ,則 令則且所以當且僅當,即時”成立.所以的最小值是2.5. (1)當k=0或k=-1或k=4時，C表示直線；當k0且k-1且k4時方程為即是0<k<2或2<k<4（）若存在，設直線PQ的方程為：y=-x+m方程（2）的>0，存在滿足條件的P、Q，直線PQ的方程為6. (1)由橢圓的定義，點P的軌跡是以M、N為焦點，長軸長2a=6的橢圓.因此半焦距c=2，長半軸a=3，從而短半軸b=，所以橢圓的方程為 (2)由得 因為不為橢圓長軸頂點，故P、M、N構成三角形.在PMN中， 將代入，得故點P在以M、N為焦點，實軸長為的雙曲線上.由(1)知，點P的坐標又滿足，所以由方程組 解得即P點坐標為7. 解：（I），是直線與雙曲線兩條漸近線的交點， ， 即2分 雙曲線的焦距為4，4分 解得， 橢圓方程為5分 （II）解：設橢圓的焦距為，則點的坐標為 ， 直線的斜率為，直線的斜率為， 直線的方程為7分 由 解得 即點設由， 得 即 10分。點在橢圓上，12分 ， 橢圓的離心率是。8. （）由，設，則問題（）轉化為方程在區間上有唯一解：若，此時，當且僅當，即適合；若，則；若，此時，當且僅當，即時適合；若，此時，但，從而。綜