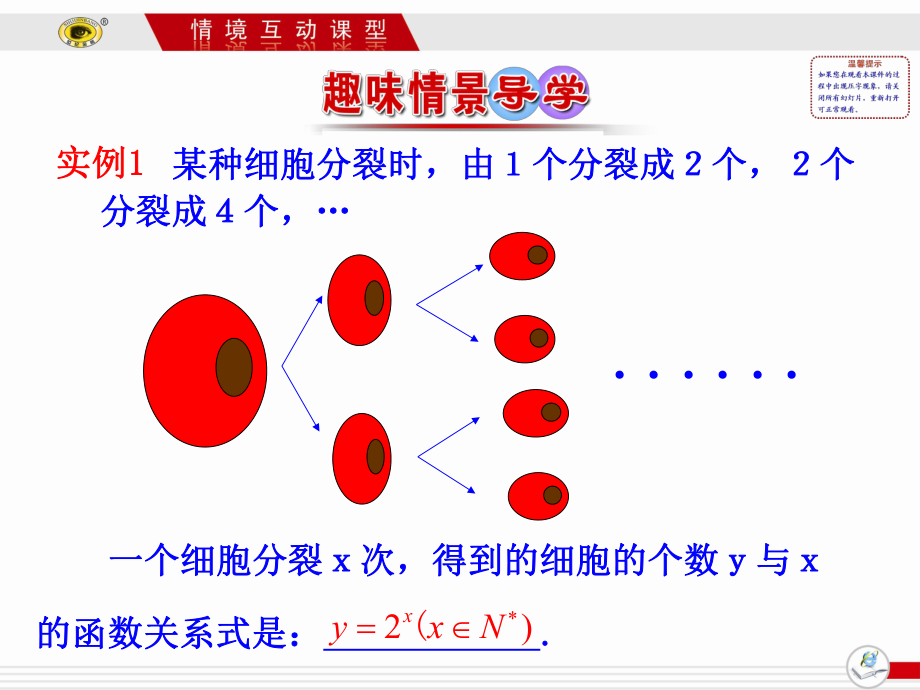
1、2.1.2 指數函數及其性質 第1課時 指數函數的圖象及性質 一個細胞分裂次，得到的細胞的個數與一個細胞分裂次，得到的細胞的個數與的函數關系式是：的函數關系式是： . .2)(xyxN實例實例1 1 某種細胞分裂時，由個分裂成個，個某種細胞分裂時，由個分裂成個，個分裂成個，分裂成個， 莊子莊子逍遙游逍遙游記載：一尺之椎，日取其記載：一尺之椎，日取其半，萬世不竭半，萬世不竭. .意思是一尺長的木棒，一天截取一意思是一尺長的木棒，一天截取一半，很長時間也截取不完半，很長時間也截取不完. .這樣的一個木棒截取這樣的一個木棒截取x x次，剩余長度次，剩余長度y y與與x x的關系是的關系是 . 12)

2、（ ） (xxNy實例實例2 2這個式子是這個式子是怎么得出來怎么得出來的呢？的呢？截取截取次數次數木棒木棒剩余剩余1次次2次次3次次4次次x次次尺21尺41尺81尺161尺x)21()()21(*Nxyx實例實例1 1和實例和實例2 2涉及的函數有什么共同特點呢？涉及的函數有什么共同特點呢？接下來我們一起來探究這個問題接下來我們一起來探究這個問題. .1.1.理解指數函數的概念理解指數函數的概念 ； （重點）重點）2.2.掌握指數函數的圖象和性質掌握指數函數的圖象和性質 ； （重點、難點）重點、難點）3.3.培養學生實際應用函數的能力；培養學生實際應用函數的能力； 形如形如y=2y=2x x

3、， 的函數是指數函數的函數是指數函數. .那那么，指數函數是怎樣定義的呢？么，指數函數是怎樣定義的呢？12xy （ ） 一般地，函數一般地，函數_（a a，且，且aa）叫做指數函）叫做指數函數，其中數，其中x x是自變量，函數的定義域是是自變量，函數的定義域是_._.探究點探究點1 1y=ay=ax xR R指數函數的概念：指數函數的概念：思考：思考：在指數函數在指數函數y=ay=ax x中，為什么要規定中，為什么要規定a0,a0,且且 a1 a1呢？呢？提示：提示：若若a=0a=0， 若若a a0 0，比如，比如y=(-4)y=(-4)x x，這時對于，這時對于x= (x= (nNnN* *

4、) ) 在實數范圍內函數值無意義在實數范圍內函數值無意義. . 若若a=1a=1,y=1,y=1x x=1=1是一個常量，因此對它就沒有研是一個常量，因此對它就沒有研 究的必要，究的必要，xxx 0a0 x 0a當 時，恒等于，當 時，無意義12n為了避免上述各種情況，所以規定為了避免上述各種情況，所以規定a a0 0且且a1.a1.21yx（ ）；23xy （ ）；34xy （ ）；(4)3;xy 21(5).xyx. .（2 2）例例1 1 下列函數中是指數函數的函數序號是下列函數中是指數函數的函數序號是1xya 冪系數為冪系數為1 1底數為正數且底數為正數且不為不為1 1的常數的常數自變

5、量僅有自變量僅有這一種形式這一種形式例例2 2 已知指數函數已知指數函數 f(xf(x)=)=a ax x(a(a0,0,且且a a1)1) 的圖象的圖象經過點經過點(3,)(3,)，求，求f(0)f(0)，f(1)f(1)，f(-3)f(-3)的值的值. .解析：解析：指數函數的圖象經過點指數函數的圖象經過點(3,)(3,)，有，有f(3)=f(3)=，即即 a a3 3=， 解得解得于是于是13a x3f x 所以所以101331(0)1,(1),( 3)fff關鍵條件關鍵條件用用 描點法描點法 作出下列兩組函數的圖象，作出下列兩組函數的圖象，然后寫出其一些性質：然后寫出其一些性質：12x

6、y ()探究點探究點2 2 研究函數都會研究函數圖象，如何畫出研究函數都會研究函數圖象，如何畫出指數函數的圖象呢？指數函數的圖象呢？x x-2-2-1.5-1.5-1-1-0.5-0.50 00.50.51 11.51.52 2y=2y=2x x0.250.25 0.350.350.50.50.710.711 11.411.412 22.832.834 4描點法是作描點法是作函數圖象的函數圖象的通用方法哦通用方法哦2xy 011xy011xy12xy12（）xy x x-2-2-1.5-1.5-1-1-0.5-0.50 00.50.51 11.51.52 24 42.832.832 21.41

7、1.411 10.710.710.50.50.350.350.250.2512xy0.0370.110.3313927y=3-x279310.330.110.037y=3x3210-1-2-3x(2) (2) 與與 的圖象的圖象. . 列表：列表：3xy 1( )3xy 同坐標系中畫出兩函數圖象，并觀察圖象的特點同坐標系中畫出兩函數圖象，并觀察圖象的特點3xy011xy13xy關于關于y y軸對稱軸對稱都過定都過定點（點（1,01,0）3xy2xy 011xy12xy13xy關于關于y y軸對稱軸對稱都過定點都過定點（1,01,0）011xy12xy13xy2xy 3xy 011xyxy010

8、1xyy=ax (0a1)xy01xya(01)a01xya(1)a xy 圖象共同特征：圖象共同特征：（1 1）圖象可向左、右兩方無限伸展）圖象可向左、右兩方無限伸展（3 3）都經過坐標為（）都經過坐標為（0 0，1 1）的點）的點（2 2）圖象都在）圖象都在x x軸上方軸上方圖象自左至右逐漸上升圖象自左至右逐漸上升圖象自左至右逐漸下降圖象自左至右逐漸下降（2 2）在）在R R上是上是減函數減函數（1 1）過定點（）過定點（0 0，1 1），即），即x=0 x=0時，時，y=1y=1 性質性質（0 0，+） 值域值域R R定義定義域域圖象圖象a1a10a10a1探究點探究點3 3 由函數圖象

9、可以得出函數的哪些性質呢？由函數圖象可以得出函數的哪些性質呢？（2 2）在）在R R上是上是增函數增函數 01xya(1)a xyxy01xyaa a決定決定單調單調性性(0a1)【總結提升總結提升】指數函數圖象和性質的巧記指數函數圖象和性質的巧記(1)(1)指數函數圖象的巧記方法指數函數圖象的巧記方法: : 一定二近三單調一定二近三單調, , 兩類單調正相反兩類單調正相反. .(2)(2)指數函數性質的巧記方法指數函數性質的巧記方法: : 非奇非偶是單調非奇非偶是單調, , 性質不同因為性質不同因為a, a, 分清比分清比1 1大或小大或小, , 依靠圖象記性質依靠圖象記性質. . 2.53

10、0.10.20.33.11 1.7,1.7 ; 2 0.8, 0.8;3 1.7, 0.9.例例3.3.比較下列各題中兩個值的大小比較下列各題中兩個值的大小解：解：(1)(1)根據函數根據函數y=1.7y=1.7x x的性質，的性質，1.71.72.52.51.71.73 3. .(2)(2)根據函數根據函數y=0.8y=0.8x x的性質，的性質，0.80.8-0.1-0.10.81.71.70 0=1=1，根據函數根據函數y=0.9y=0.9x x的性質，的性質，0.90.93.13.10.90.90.93.13.1根據指數根據指數函數的性函數的性質質不同底的要找中間值不同底的要找中間值0

11、14（ ）3514（ ）230 19. 00 19.用用“”或或“”填空：填空：5643（ ）043（ ）745 06. 05 06.【變式練習變式練習】1.1.下列以下列以x x為自變量的函數中為自變量的函數中, ,是指數函數的是是指數函數的是( )( )2.( 4).2 4.(01)xxxxA yB yC yD yaaa 且B B2.2.若函數若函數y=y=（a a2 2-3a+3-3a+3）a ax x是指數函數，則（）是指數函數，則（）A Aa a1 1且且a1a1 B Ba=1a=1C Ca=1a=1或或a=2a=2 D Da=2a=2【解析解析】若函數若函數y=y=（a a2-3a

12、+3-3a+3）a ax是指數函數，是指數函數，則則a a2-3a+3=1-3a+3=1，解得解得a=2a=2或或a=1a=1，又因為指數函數的底數又因為指數函數的底數a a0 0且且a1a1，故故a=2.a=2.D D定義是考定義是考查的重點查的重點3.3.函數函數y=ay=ax-3+2+2（a a0 0且且a1a1）的圖象一定經過點）的圖象一定經過點P P，則，則P P點的坐標為（）點的坐標為（）A.A.（-2-2，-3-3） B.B.（3 3，3 3）C.C.（3 3，2 2） D.D.（-3-3，-2-2）【解析解析】因為因為y=ay=ax-3x-3+2+2（a a0 0且且a1a1）

13、，），所以當所以當x-3=0 x-3=0，即，即x=3x=3時，時，y=3y=3，所以函數所以函數y=ay=ax-3x-3+2+2（a a0 0且且a1a1）的圖象過定點）的圖象過定點P P（3 3，3 3）. .B B【解析解析】解法解法1 1, ,大于，且大于，且, ,大于小于大于小于且且4.4.如圖如圖, ,指數函數指數函數:A. :A. y= =ax x B.B.y= =bx x C.C.y= =cx x D. D. y= =dx x的圖象的圖象, ,則則a, ,b, ,c, ,d與與1 1的大小關系是的大小關系是_._. xyBDCAO結論：當結論：當a11時時, ,圖象越靠近圖象越靠近軸，底數越大軸，底數越大; ; 當當00a1d1abcd1abxyBDCAO1.E.F.G.H5.5.已知指數函數已知指數函數f f（x x）的圖象過點（）的圖象過點（3 3，8 8），），求求f f（6 6）的值）的值【解析解析】設指數函數為：設指數函數為：f f（x x）= =a ax x(a(a00且且a a1)1)，因為指數函數因為指數函數f f（x x）的圖象過點（）的圖象過點（3 3，8 8），），所以所以8=a8=a3 3，所以，所以a=2a=2，所以所以f f（x x）=2=2x