1、文檔供參考，可復(fù)制、編制，期待您的好評(píng)與關(guān)注！ 平面向量基本定理和坐標(biāo)表示【知識(shí)清單】1 兩個(gè)向量的夾角（1）已知兩個(gè)_向量，在平面內(nèi)任取一點(diǎn),作，則叫做向量與的夾角（2）向量夾角的范圍是_，當(dāng)_時(shí)，兩向量共線，當(dāng)_時(shí)，兩向量垂直，記作2平面向量基本定理及坐標(biāo)表示（1）平面向量基本定理如果是同一平面內(nèi)的兩個(gè)_向量，那么對(duì)于這一平面內(nèi)的任意向量，_一對(duì)實(shí)數(shù)，使_其中，不共線的向量叫做表示這一平面內(nèi)所有向量的一組_（2）平面向量的正交分解及坐標(biāo)表示把一個(gè)向量分解為兩個(gè)_的向量，叫做把向量正交分解（3） 平面向量的坐標(biāo)表示在平面直角坐標(biāo)系中，分別取與軸、軸方向相同的兩個(gè)單位向量i，j作為基底，對(duì)于平

2、面內(nèi)的一個(gè)向量，由平面向量基本定理可知，有且只有一對(duì)實(shí)數(shù)，使，這樣，平面內(nèi)的任一向量都可由，唯一確定，把有序數(shù)對(duì)_叫做向量的坐標(biāo)，記作_，其中_叫做在軸上的坐標(biāo)，_叫做在軸上的坐標(biāo) ，則向量的坐標(biāo)就是_的坐標(biāo)，即若， 則A點(diǎn)坐標(biāo)為_(kāi)，反之亦成立（O是坐標(biāo)原點(diǎn)）3平面向量的坐標(biāo)運(yùn)算向量加法和減法若則實(shí)數(shù)與向量的乘積若則向量的坐標(biāo)若起點(diǎn)終點(diǎn)則 4平面向量共線的坐標(biāo)表示設(shè)，其中，_1.已知平面向量，且，則（     ）A     B     C   &

3、#160;  D 2.下列向量組中，能作為平面內(nèi)所有向量基底的是（    ）A.       B. C.       D. 6 / 63.已知，則與平行的單位向量為(   ).A. B.   C.       D.4.連續(xù)拋擲兩次骰子得到的點(diǎn)數(shù)分別為和，記向量，向量，則的概率是（    ）    

4、A  B  C    D5.平面向量=（2，-1），=（1，1），=（-5，1），若，則實(shí)數(shù)k的值為（）A2   B. C. D.6.已知A（3，0）、B（0，2），O為坐標(biāo)原點(diǎn)，點(diǎn)C在AOB內(nèi)，且AOC45°，設(shè)，則的值為（     ） A、   B、 C、   D、7.在下列向量組中，可以把向量表示出來(lái)的是（    ）A.      

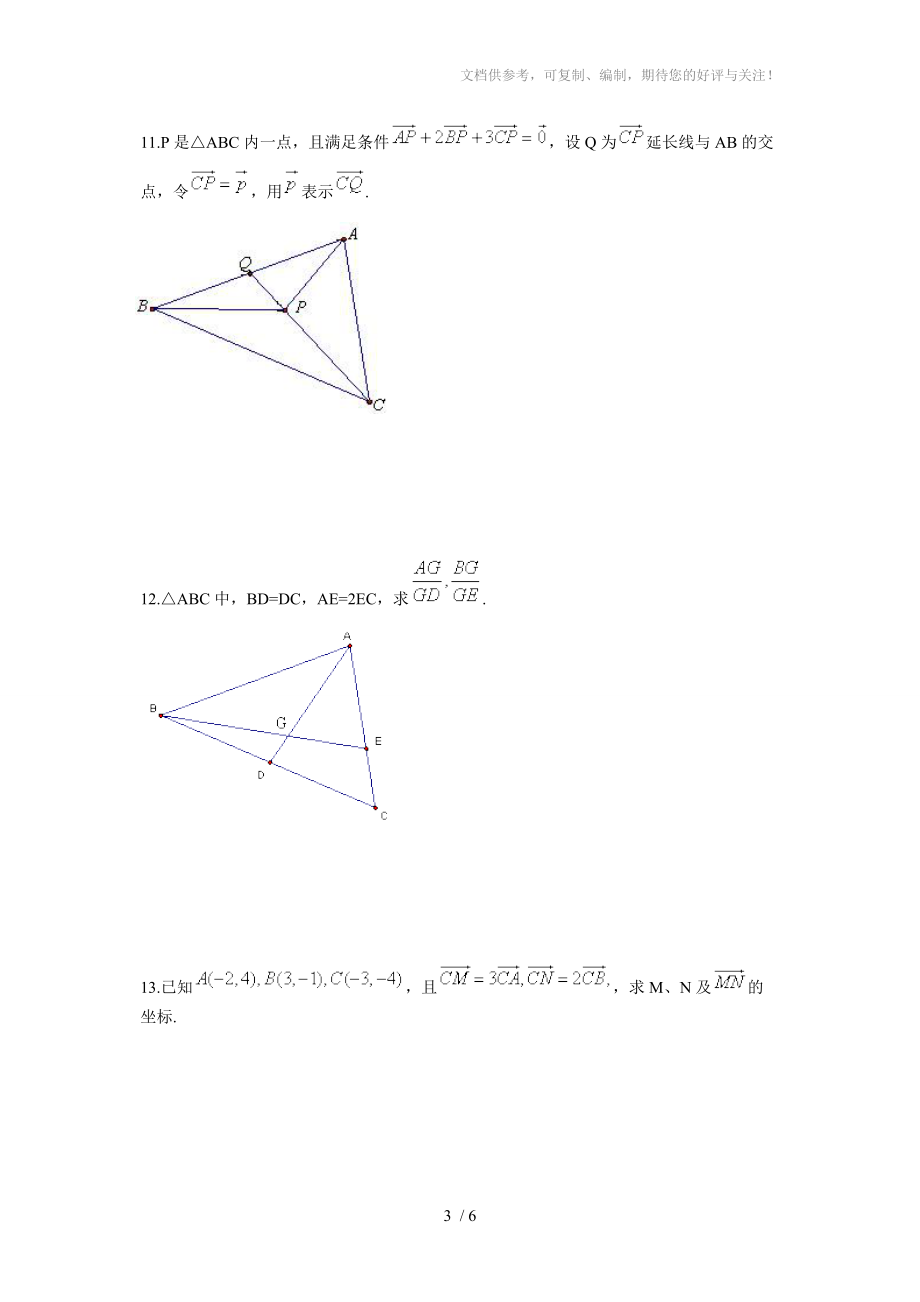
5、    B .    C.          D. 8.已知直角坐標(biāo)平面內(nèi)的兩個(gè)向量，使得平面內(nèi)的任意一個(gè)向量都可以唯一分解成，則的取值范圍      9.,若，則   ;若,則   10.向量，若向量與向量共線，則  .11.P是ABC內(nèi)一點(diǎn)，且滿足條件，設(shè)Q為延長(zhǎng)線與AB的交點(diǎn)，令，用表示.12. ABC中，BD=DC，AE

6、=2EC，求.13. 已知，且，求M、N及的坐標(biāo).14. i、j是兩個(gè)不共線的向量,已知=3i+2j，=i+j, =-2i+j,若A、B、D三點(diǎn)共線,試求實(shí)數(shù)的值15.已知向量，向量. （1）若向量與向量垂直，求實(shí)數(shù)的值；（2）當(dāng)為何值時(shí)，向量與向量平行？并說(shuō)明它們是同向還是反向.16.在中，分別是內(nèi)角的對(duì)邊，且，,若.（1）求的大小；（2）設(shè)為的面積，求的最大值及此時(shí)的值.平面向量基本定理及坐標(biāo)表示答案BBBABCB8. 9.  ， 10.211又因?yàn)锳，B，Q三點(diǎn)共線，C，P，Q三點(diǎn)共線而，為不共線向量故：12.設(shè)又又而比較，由平面向量基本定理得：解得：或（舍） ，把代入得：.13.：設(shè)，則同理可求，因此14，=-=(-2i+j)-(i+j)=-3i+(1-)jA、B、D三點(diǎn)共線,向量與共線,因此存在實(shí)數(shù),使得=,即3i+2j=-3i+(1-)j=-3i+(1-)ji與j是兩不共線向量,由基本定理得:故當(dāng)A、B、D三點(diǎn)共線時(shí),=3.15.解：，.（1）由向量與向量垂直，得，解得.             &