第六章函數(shù)插值6.1 代數(shù)插值設(shè)已知某個函數(shù)關(guān)系y=f(x)在某些離散點上的函數(shù)值：

插值問題：

根據(jù)這些已知數(shù)據(jù)來構(gòu)造函數(shù)y=f(x)的一種簡單的近似表達式以便于計算點的函數(shù)值，或計算函數(shù)的一階、二階導(dǎo)數(shù)值。(6.1)選取多項式Pn(x)，使得（6.2）

作為f(x)的近似。

滿足關(guān)系（6.2）的函數(shù)Pn(x)為f(x)的一個插值函數(shù)，x0,x1,…,xn

為插值節(jié)點，關(guān)系（6.2）為插值原則。這種用代數(shù)多項式作為工具來研究插值的方法叫做代數(shù)插值設(shè)

x0<x1<…<xn記a=x0,b=xn，則[a,b]

為插值區(qū)間。插值多項式的存在唯一性：設(shè)所要構(gòu)造的插值多項式為：由插值條件得到如下線性代數(shù)方程組：此方程組的系數(shù)行列式為范得蒙行列式！當

時，

D

0，因此，Pn(x)由a0,a1,…,an唯一確定。定理(唯一性)滿足的n

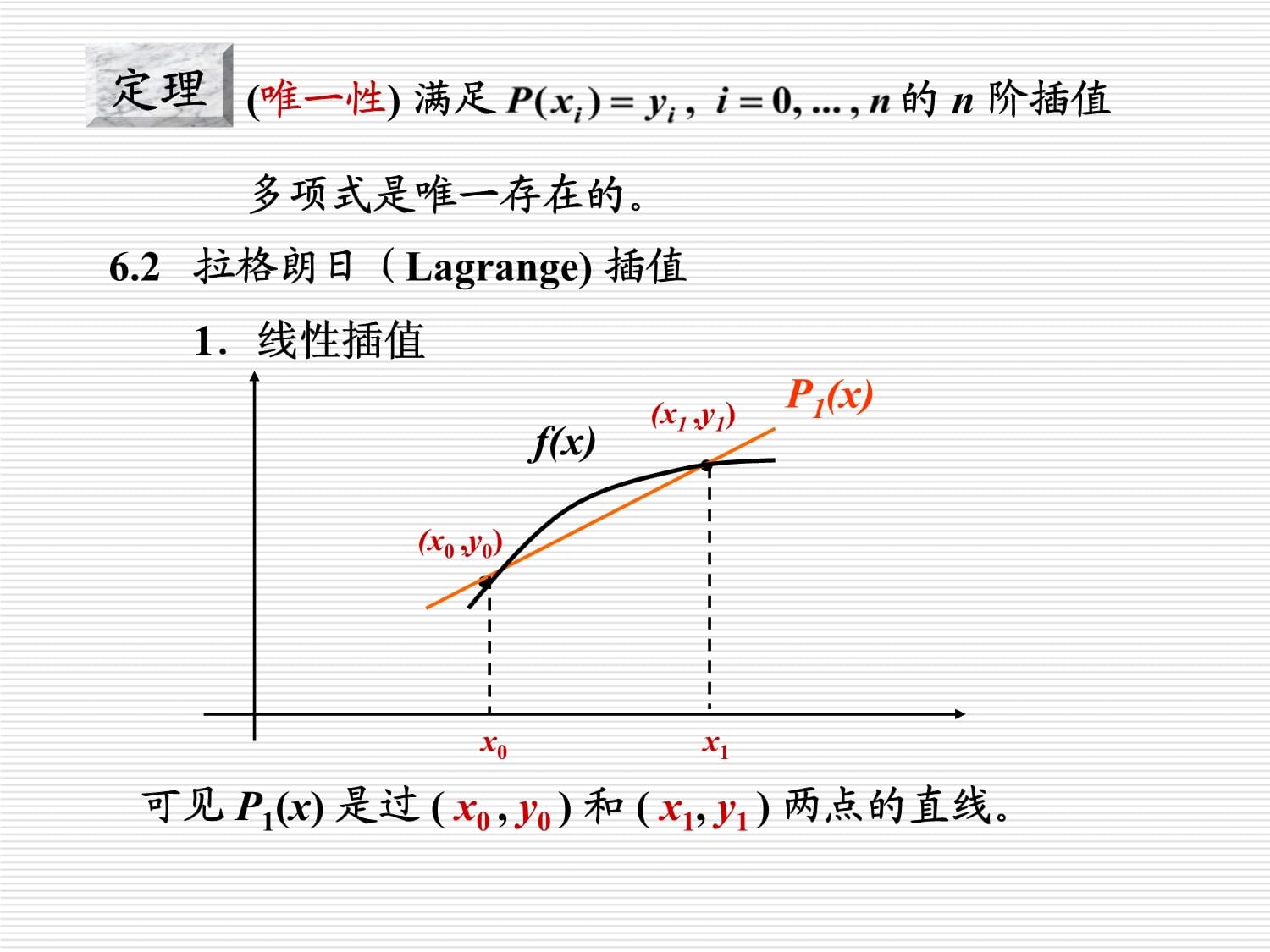
階插值多項式是唯一存在的。6.2拉格朗日（Lagrange)插值1．線性插值

x0x1(x0,y0)(x1

,y1)P1(x)f(x)可見P1(x)是過(x0,y0

)和(x1,y1

)兩點的直線。x0x1x2p2(x)

f(x)f(x)2．拋物插值因過三點的二次曲線為拋物線，故稱為拋物插值。

要求：無重合節(jié)點，即3．拉格朗日插值公式設(shè)連續(xù)函數(shù)y=f（x）在[a,b]上對給定n+1個不同結(jié)點：x0,x1,…,xn分別取函數(shù)值y0,y1,…,yn其中

yi=f(xi)i=0,1,2,…,n試構(gòu)造一個次數(shù)不超過n的插值多項式使之滿足條件

i=0,1,2,…,n求n次多項式lk(x)k=0,1,…,n則

i=0,1,2,…,n即Pn(x)滿足插值條件（6.2）

根據(jù)lk(x)的表達式，xk以外所有的結(jié)點都是lk(x)的根，又由lk(xk)=1，得：

因此令從而得n階拉格朗日（Lagrange）插值公式：4插值余項在[a,b]內(nèi)存在,考察截斷誤差設(shè)節(jié)點，且f

滿足條件,

存在使得。且推廣：若使得使得羅爾定理:若在［］連續(xù)，在充分光滑，注：

通常不能確定x

,而是估計,x(a,b)

將作為誤差估計上限。當

f(x)為任一個次數(shù)n

的多項式時，,可知，即插值多項式對于次數(shù)n的多項式是精確的。6.3牛頓插值Lagrange插值雖然易算，但若要增加一個節(jié)點時，全部基函數(shù)li(x)都需重新算過。以拋物插值為例介紹牛頓插值：設(shè)：

i=0,1,2也可以將P2(x)寫成：令x=x1，由（6.2），有令x=x0，由插值條件（6.2），有最后，由 得1．差商的定義定義1：設(shè)有函數(shù)f(x)以及自變量的一系列互不相等的x0,x1,…,xn

（即在ij時，xi

xj）的值

f(xi)

,

稱為f(x)在點xi,xi處的一階差商，并記作f[xi,xj]，

又稱為f(x)在點xi,xj,xk處的二階差商

稱

為f(x)在點x0,x1,…,xn處的n階差商。f(x0)f(x1)f(x2)…f(xn1)f(xn)f[x0,x1]f[x1,x2]…………f[xn1,xn]f[x0,x1,x2]…………f[xn2,xn1,xn]f[x0,…,xn]

xn+1f(xn+1)f[xn,xn+1]f[xn1,xn,xn+1]f[x1,…,xn+1]f[x0,…,xn+1]差商可列表計算：xi

yi

一階差商

二階差商

n階差商

……由差商定義可知：高階差商是兩個低一階差商的差商。x0x1x2xn-1xn2牛頓插值公式12…………n1(x

x0),2……(x

x0)…(x

xn1)n1Nn(x)Rn(x)ai=

f[x0,…,xi]牛頓插值公式的優(yōu)點是：當增加一個節(jié)點時，只要再增加一項就行了，即有遞推式:由插值的唯一性可知Nn(x)Ln(x)，故其余項也相同，即差商與導(dǎo)數(shù)的關(guān)系公式

6.4差分及其性質(zhì)，等距節(jié)點插值公式1．微商的離散化引入符號向前差分向后差分

中心差分

一階差商當h充分小或當xj充分靠近xi時，有在幾何圖形上，這三種差商分別表示弦AB、AC和BC的斜率。將這三條弦線與過點A的切線相比較，從圖形上可以看出，一般地說，弦BC的斜率更接近于切線斜率f’(a)。等距節(jié)點公式向前差分iiifff-=+1ikikikikffff1111)(-+---==向后差分111----=ikikikfffi1iifff-=中心差分其中當節(jié)點等距分布時:（k個差分因子）差分的重要性質(zhì)：性質(zhì)3：若f(x)是m

次多項式，則是性質(zhì)1：常數(shù)的差分等于零性質(zhì)2：差分算子為線性算子次多項式，且性質(zhì)4：

這個性質(zhì)類比于性質(zhì)5：

（類比于分部積分法則）性質(zhì)6：當節(jié)點xk是等距時，差分差商存在著關(guān)系：差分值可由函數(shù)值算出：=-+-=Dnjjknjknfjnf0)1(其中=-+--=njnjkjnknfjnf0)1(牛頓公式牛頓前差公式牛頓后差公式將節(jié)點順序倒置：設(shè)，則)()()(000xfkthtxNxNknknn=+==設(shè)，則)()1()()(0nknkknnnxfkthtxNxN--=+==注：一般當x

靠近x0時用前插，靠近xn

時用后插，故兩種公式亦稱為表初公式和表末公式。6.5Hermite

插值多項式要求函數(shù)值重合，而且要求若干階導(dǎo)數(shù)也重合。即：要求插值函數(shù)P(x)

滿足p(xi)=f(xi),P’(xi)=f’(xi),…,P(m)(xi)=f

(m)(xi).

在實際問題中，對所構(gòu)造的插值多項式，不僅把此類插值多項式稱為埃米爾特（Hermite）插值多項式或稱帶導(dǎo)數(shù)的插值多項式，記為H(x)。

注：

N

個條件可以確定階多項式。要求在1個節(jié)點x0處直到m0

階導(dǎo)數(shù)都重合的插值多項式即為Taylor多項式其余項為N

1例：設(shè)x0

x1x2,已知f(x0)、f(x1)、f(x2)

和f’(x1),求多項式P(x)模仿Lagrange多項式的思想，設(shè)解：首先，P

的階數(shù)=3+=213)()()()()(=0iiixhx1f’xhxfxPh0(x)有根x1,x2，且h0’(x1)=0x1是重根。)()()(22100xxxxCxh--=又:h0(x0)=1C0h2(x)h1(x)有根x0,x2

))()(()(201xxxxBAxxh--+=由余下條件h1(x1)=1和

h1’(x1)=0可解。與h0(x)完全類似。

(x)h1有根x0,x1,x2

h1))()(()(2101xxxxxxCx---=h1又:’(x1)=1C1

可解。其中hi(xj)=ij,hi’(x1)=0,

(xi)=0,

’(x1)=1h1h1與Lagrange分析完全類似滿足P(xi)=f(xi)，i=0,1,2，且P’(x1)=f’(x1),并估計誤差。一般地，已知x0

,…,xn

處有y0

,…,yn

和y0’

,…,yn’，求H2n+1(x)解：設(shè)+=ni)()()(=0iixhxhyixH2n+1n=0iyi’其中hi(xj)=ij,hi’(xj)=0,

(xj)=0,

’(xj)=ij

hihihi(x)有根x0

,…,xi,…,xn且都是2重根)()()(2xlBxAxhiiii+=由余下條件hi(xi)=1和

hi’(xi)=0可解Ai

和Bi

(x)hi有根x0

,…,xn,除了xi

外都是2重根hi)()(iili2(x)xxCx-=hi又:’(xi)=1Ci

=1hi)(x)(ili2(x)xx-=設(shè)則這樣的Hermite

插值唯一滿足H2n+1(xi)=yi

，H’2n+1(xi)=yi’。牛頓――埃米爾特多項式例1

已知函數(shù)表

y1y0y

x1

x0

x

求一個插值多項式H(x)，使其滿足如下條件：解：先由函數(shù)表xx0x1y

y0y1作線性插值，即為再注意到H(x)與P1(x)在節(jié)點x0,x1上函數(shù)值相同，

于是，它們的差可以設(shè)為其中K為待定常數(shù)，上式又可記為：

為確定K，對上式求導(dǎo)：

令x=x0，代入上式，并且注意到插值條件

得：

于是有牛頓――埃米爾特多項式的構(gòu)造方法:

已知函數(shù)表求一個插值多項式H(x)，使其滿足如下條件：插值條件的個數(shù)：m+n+2H(x)的次數(shù)：不超過m+n+1次

i=0,1,2,…,n

（6.3）i=0,1,2,…,m

（6.4）按牛頓插值的構(gòu)造思想，設(shè)

其中Nn

(x)是牛頓基本插值多項式；Pm(x)為特定的m次多項式。顯然：

i=0,1,2,…,n

為確定Pm(x)，對（6.5）求導(dǎo)（6.5）（6.6）令x=xi,i=0,1,2,…,m，將條件（6.4），代入（6.6）得所以

i=0,1,2,…,

于是，求Pm(x)的問題，變成已知Pm(x)的函數(shù)表xx0x1x2…xmPm(x)Pm(x0)Pm(x1)Pm(x2)

Pm(xm)確定一個次數(shù)不超過m的插值多項式Lm(x)，使其滿足

i=0,1,2,…,m因為Pm(x)為小于等于m次多項式。所以，令x–x-1=1，將上式代入（6.5），便得到滿足插值條件的埃米爾特插值多項式

6.6分段低次插值例：在[5,5]上考察的Ln(x)。取

-5

-4

-3

-2

-1

0

1

2

3

4

5

-0.5

0

0.5

1

1.5

2

2.5

n

越大，端點附近抖動越大，稱為Runge

現(xiàn)象Ln(x)f(x)分段低次插值

分段線性插值在每個區(qū)間上，用1階多項式

(直線)逼近f(x):記，易證：當時，一致失去了原函數(shù)的光滑性。yxoy=f(x)y=p(x)分段Hermite插值給定在上利用兩點的y及y’構(gòu)造3次Hermite函數(shù)導(dǎo)數(shù)一般不易得到。6.7樣條函數(shù)插值要求：插值曲線即要簡單，又要在曲線的連接處比較光滑。

這樣的分段插值函數(shù)在分段上要求多項式次數(shù)低，而在節(jié)點上不僅連續(xù)，還存在連續(xù)的低階導(dǎo)數(shù)，我們把滿足這樣條件的插值函數(shù)，稱為樣條插值函數(shù)，它所對應(yīng)的曲線稱為樣條曲線，其節(jié)點稱為樣點，這種插值方法稱為——樣條插值。方磚砌圓井

條石筑拱橋定義：設(shè)對y=f(x)在區(qū)間[a,b]上給定一組節(jié)點a=x0<x1<x2<…<xn

=b和相應(yīng)的函數(shù)值y0,y1,…,yn，如果s(x)具有如下性質(zhì)：（1）在每個子區(qū)間[xi-1,xi](i=1,2,…,n)上s(x)是不高于三次的多項式； （2）s(x)，s’(x)，s(x)在[a,b]上連續(xù)；則稱s(x)為三次樣條函數(shù)。如再有（3）(i=0,1,2,…,n)，則稱s(x)為y=f(x)的三次樣條插值函數(shù)。f(x)H(x)S(x)注：三次樣條與分段Hermite

插值的根本區(qū)別在于S(x)自身光滑，不需要知道f的導(dǎo)數(shù)值（除了在2個端點可能需要）；而Hermite

插值依賴于f在所有插值點的導(dǎo)數(shù)值。三次樣條插值的存在唯一性和計算方法設(shè)f(x)是定義在

[a,b]區(qū)間上的一個二次連續(xù)可微函數(shù)，為分劃：S(x)在

[xi-1,xi]上的表達式為：令i=0,1,2,…,n在每一個小區(qū)間[xi-1,xi]i=1,…,n

上都是三次多項式，（6.7）其中，將（6.7）兩次積分得：Ai