

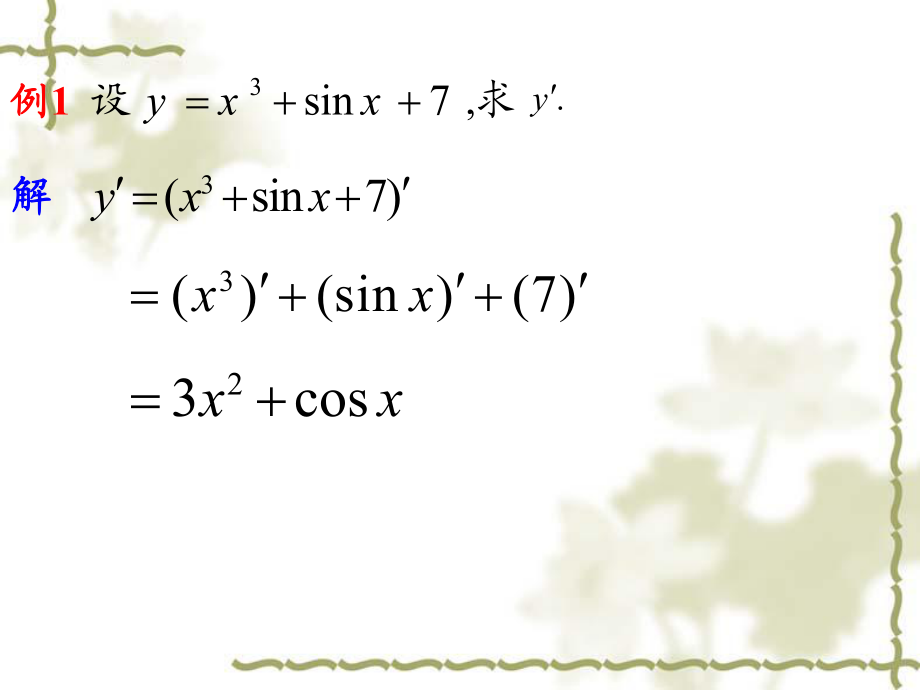


版權(quán)說明:本文檔由用戶提供并上傳,收益歸屬內(nèi)容提供方,若內(nèi)容存在侵權(quán),請進(jìn)行舉報或認(rèn)領(lǐng)
文檔簡介
1、第二節(jié)第二節(jié)二、高階導(dǎo)數(shù)二、高階導(dǎo)數(shù) 三、復(fù)合函數(shù)求導(dǎo)法則三、復(fù)合函數(shù)求導(dǎo)法則 一、導(dǎo)數(shù)的四則運(yùn)算法則一、導(dǎo)數(shù)的四則運(yùn)算法則 函數(shù)的求導(dǎo)法則函數(shù)的求導(dǎo)法則 第三章第三章 四、反函數(shù)求導(dǎo)法則四、反函數(shù)求導(dǎo)法則 五、隱函數(shù)求導(dǎo)法則五、隱函數(shù)求導(dǎo)法則 六、對數(shù)求導(dǎo)法則六、對數(shù)求導(dǎo)法則 七、參數(shù)方程的求導(dǎo)法則七、參數(shù)方程的求導(dǎo)法則 一、導(dǎo)數(shù)的四則運(yùn)算法則(一、導(dǎo)數(shù)的四則運(yùn)算法則(P43) 定理定理1.具有導(dǎo)數(shù)都在及函數(shù)xxvvxuu)()()()(xvxu及的和、的和、 差、差、 積、積、 商商 (除分母除分母為為 0的點(diǎn)外的點(diǎn)外) 都在點(diǎn)都在點(diǎn) x 可導(dǎo)可導(dǎo), 且且)()( )()() 1 (xvx
2、uxvxu)()()()( )()()2(xvxuxvxuxvxu)()()()()()()()3(2xvxvxuxvxuxvxu)0)(xv推廣:推廣:有限個函數(shù)和差的導(dǎo)數(shù)等于其導(dǎo)數(shù)的和差。有限個函數(shù)和差的導(dǎo)數(shù)等于其導(dǎo)數(shù)的和差。 注:注:此法則可推廣到有限個可導(dǎo)函數(shù)之積的情形。此法則可推廣到有限個可導(dǎo)函數(shù)之積的情形。 )( )(xuCxCu推論:推論:3(sin7)yxx23cosxx3()(sin )(7)xx.y例例1 設(shè),求解解7sin3xxy3(coslnsin5)yxxx3( )(cos )(ln )(sin5)xxxxxx1sin323coslnsin5yxxx.y例例2 設(shè),求
3、解解 例例3 3 設(shè) ,求 解解 xxy2y)2(xxy2ln222xxxx)2(2)(xxxx例 4設(shè)sinlnyxxx,求y( ) sin ln(sin ) lnsin (ln )xxxxxxxxxsin lncos lnsinxxxxxxyexyx求已知例5.)(xexy解:2)()(xxxeexexxex12)(xxxexee 例 6設(shè)1 sin,1 cosxyyx求解解 1 sin1 cosxyx2(1 sin ) (1 cos )(1 sin )(1 cos )(1 cos )xxxxx2cos (1 cos )(1 sin )( sin )(1 cos )xxxxx222cosc
4、ossinsin(1 cos )xxxxx21 cossin(1 cos )xxx 定義定義. 若函數(shù)若函數(shù))(xfy 的導(dǎo)數(shù)的導(dǎo)數(shù))(xfy可導(dǎo)可導(dǎo), ,或或,dd22xy即即)( yy或或)dd(dddd22xyxxy記作記作y )(xf的的二階導(dǎo)數(shù)二階導(dǎo)數(shù) ,)(xf 的導(dǎo)數(shù)為的導(dǎo)數(shù)為注:注:則稱則稱1.二階導(dǎo)數(shù)的概念二階導(dǎo)數(shù)的概念二、二、高階導(dǎo)數(shù)高階導(dǎo)數(shù)稱為一階導(dǎo)數(shù)。)(xf 二階導(dǎo)數(shù)的導(dǎo)數(shù)二階導(dǎo)數(shù)的導(dǎo)數(shù)稱為稱為三階導(dǎo)數(shù)三階導(dǎo)數(shù)。1n階導(dǎo)數(shù)的導(dǎo)數(shù)階導(dǎo)數(shù)的導(dǎo)數(shù)稱為稱為 n 階導(dǎo)數(shù)階導(dǎo)數(shù) 。,y ,)4(y)(,ny或或,dd33xy,dd44xynnxydd,分別記作:分別記作:二階及二
5、階以上的導(dǎo)數(shù)統(tǒng)稱為二階及二階以上的導(dǎo)數(shù)統(tǒng)稱為高階導(dǎo)數(shù)。高階導(dǎo)數(shù)。2.高階導(dǎo)數(shù)高階導(dǎo)數(shù)例例1 1解解211xy )11(2 xy22)1(2xx .,arctanyxy 求設(shè)例例2 2ybaxy 求設(shè),)(abaxy0)( ay解解2222)1 ()1 (1)1 (0 xxx三、復(fù)合函數(shù)的求導(dǎo)法則三、復(fù)合函數(shù)的求導(dǎo)法則(P44)dxdududydxdyxufxfxxfyuufyxxu )( )( )( )( )( )( 或可導(dǎo),且有處在點(diǎn)處可導(dǎo),則復(fù)合函數(shù)在對應(yīng)點(diǎn)處可導(dǎo),函數(shù)在點(diǎn):若函數(shù)定理思路:思路:方法:方法:復(fù)合函數(shù)的導(dǎo)數(shù)復(fù)合函數(shù)的導(dǎo)數(shù)等于等于外層函數(shù)的導(dǎo)數(shù)外層函數(shù)的導(dǎo)數(shù)乘以乘以內(nèi)層函數(shù)的
6、導(dǎo)數(shù)內(nèi)層函數(shù)的導(dǎo)數(shù)。 由由外外層(函數(shù))向?qū)樱ê瘮?shù))向內(nèi)內(nèi)層(函數(shù))一層層求導(dǎo)。層(函數(shù))一層層求導(dǎo)。求導(dǎo)。對中間變量表示函數(shù)而求導(dǎo),對自變量表示函數(shù))( )( )( )( )( xuxfxfxxfxf例例1 1.tanln的的導(dǎo)導(dǎo)數(shù)數(shù)求求函函數(shù)數(shù)xy 解解.tan,lnxuuy 注注:)tan(lnxyxu2sec1 xxcossin1 )(tan)(lnxuxxxxx22cos1sincossectan1)1 ()(ln2 xuy21lnxuuy,解解y)1ln(2xy例例2 2 設(shè) ,求 xu21212xx的導(dǎo)數(shù)求例 sin 3xy 422的導(dǎo)數(shù)求例xayxuuy , sin解xxxux
7、uy2cos21cos)()(sin22 , xauuy解:2222)2(21()(xaxxuxauy)例例5 5.)cos(ln的導(dǎo)數(shù)的導(dǎo)數(shù)求函數(shù)求函數(shù)xey 解解xevvuuy ,cos,ln)tan()sin(1xxxeeevu 注:注:熟練以后,可以不寫出中間變量,此例可以這樣寫:熟練以后,可以不寫出中間變量,此例可以這樣寫: )cos()cos(1)cos(ln xxxeeedxdy)tan( )()cos()sin(xxxxxeeeee )()(cos)(lnxevuy解解 解解 22222121(1)2 12 11xxyxxxxx322(cos)3cos(cos )3sin co
8、syxxxxx解解 33323(cos)sin()3sinyxx xxx例例9 9.1sin的導(dǎo)數(shù)的導(dǎo)數(shù)求函數(shù)求函數(shù)xey 解解)1(sin1sin xeyx)1(1cos1sin xxex.1cos11sin2xexx 例例1010 32ln1xy)ln1 ()ln1 (3121312xxy解:解: )(ln1 )ln1 (312322xx)(lnln20 )ln1 (31322xxxxxxln12)ln1 (31322xxxln)ln1 (32322 定理定理2.42.4 如果單調(diào)連續(xù)函數(shù)如果單調(diào)連續(xù)函數(shù) 在點(diǎn)在點(diǎn)y處可導(dǎo),而且處可導(dǎo),而且 那么它的反函數(shù)那么它的反函數(shù) 在對應(yīng)點(diǎn)在對應(yīng)點(diǎn)x
9、處可導(dǎo),且有處可導(dǎo),且有 或者或者 四、反函數(shù)的求導(dǎo)法則四、反函數(shù)的求導(dǎo)法則(P35)(P35)即即 原函數(shù)的導(dǎo)數(shù)等于其反函數(shù)的導(dǎo)數(shù)的倒數(shù)原函數(shù)的導(dǎo)數(shù)等于其反函數(shù)的導(dǎo)數(shù)的倒數(shù).利用此法則的步驟:利用此法則的步驟: (1)(1)求出其反函數(shù)并判斷其在相應(yīng)區(qū)間內(nèi)求出其反函數(shù)并判斷其在相應(yīng)區(qū)間內(nèi)是否單調(diào)可導(dǎo);是否單調(diào)可導(dǎo); (2) (2)求出反函數(shù)的導(dǎo)數(shù);求出反函數(shù)的導(dǎo)數(shù);求解之。)利用公式(dydxdxdy13yxsinxyarcsin)22(,0cos)(sinyy 求函數(shù) 的導(dǎo)數(shù) xyarcsin例例1 1解解2211sin11cos1)(sin1)(arcsinxyyyx的反函數(shù)為的反函數(shù)為
10、且在且在上單調(diào)、可導(dǎo)。上單調(diào)、可導(dǎo)。例例2 求函數(shù) 的導(dǎo)數(shù) xyarctanyxtanxyarctan)22(,0sec)(tan2yy解解的反函數(shù)為的反函數(shù)為且在且在單調(diào)、可導(dǎo)。單調(diào)、可導(dǎo)。22211tan11sec1)(tan1)(arctanxyyyx解解yxalog的反函數(shù)為且在(0,+)內(nèi)單調(diào)、可導(dǎo)。例例3 3 求求 的導(dǎo)數(shù)的導(dǎo)數(shù). .1, 0aaayxxay 0ln1aydydxaaaydydxyxlnln1隱函數(shù)隱函數(shù): :.稱為隱函數(shù)由方程所確定的函數(shù)0),(yxF形式稱為顯函數(shù).)(xfy )(0),(xfyyxF隱函數(shù)的顯化顯函數(shù)的隱化顯函數(shù):顯函數(shù):五、隱函數(shù)求導(dǎo)法則五、
11、隱函數(shù)求導(dǎo)法則注:注:當(dāng)方程當(dāng)方程0)(yxF,x 的兩端對的兩端對 求導(dǎo)時,求導(dǎo)時,方法:方法:的一次方程;求導(dǎo),得到含)兩端同時對(yx1即可。)解出(y2y要記住要記住的函數(shù)。的函數(shù)。x是是例例1 1dxdyyxyey的導(dǎo)數(shù)所確定的隱函數(shù)求由方程解解求導(dǎo)方程兩邊對xyxyyeyxeyyy)()(xyey例例2 2.0dxdyyeexyyx的導(dǎo)數(shù)所確定的隱函數(shù)求由方程解解求導(dǎo)方程兩邊對x0yeeyxyyxyxexyey)0()()()(yxeexy例例3 3dxdyyyxey的導(dǎo)數(shù)所確定的隱函數(shù)求由方程22解解求導(dǎo)方程兩邊對xyyxyey22yeyxy22)()()(22yxey解解求導(dǎo)方
12、程兩邊對x例例4 4dxdyyxexexy,求已知3)()()()(3yxexexyyyeexexyy231)(yyeyxeexyy231231yxeeeyyxy例例5. 求由方程求由方程03275xxyy)(xyy 在在 x = 0 處的導(dǎo)數(shù)處的導(dǎo)數(shù).0ddxxy解解: 方程兩邊對方程兩邊對 x 求導(dǎo)求導(dǎo))0()32(75xxyyyy45y21621x025211dd46yxxyy因因 x = 0 時時 y = 0 , 故故2100252110dd46yxyxxxy確定的隱函數(shù)確定的隱函數(shù)例例6. 求橢圓求橢圓191622yx在點(diǎn)在點(diǎn))3,2(23處的切線方程處的切線方程.解解: 橢圓方程兩
13、邊對橢圓方程兩邊對 x 求導(dǎo)求導(dǎo)8xyy920yk切則2323xyyx1692323xy43故切線方程為:故切線方程為:323y43)2( x即即03843 yxyxy169練習(xí):練習(xí):xyexexyyxeyxyy、及的導(dǎo)數(shù)、隱函數(shù)2021yxxyyyxeeyeeyexyxeey12.0;112)()答案:(六、對數(shù)求導(dǎo)法六、對數(shù)求導(dǎo)法 有時會遇到這樣的情形,即雖然給出的是顯函數(shù)有時會遇到這樣的情形,即雖然給出的是顯函數(shù)但直接求導(dǎo)有困難或很麻煩但直接求導(dǎo)有困難或很麻煩觀察函數(shù)觀察函數(shù).,)4(1)1(sin23xxxyexxxy 對數(shù)求導(dǎo)法通常解決兩類問題對數(shù)求導(dǎo)法通常解決兩類問題: :的導(dǎo)數(shù)
14、。冪指函數(shù);方、開方所構(gòu)成的函數(shù)多個函數(shù)相乘、除、乘)()()2() 1 (xvxu方法方法: :(1 1)方程兩邊同時取(自然)對數(shù))方程兩邊同時取(自然)對數(shù), ,并化簡;并化簡;x(2 2)兩邊同時對)兩邊同時對 求導(dǎo),將求導(dǎo),將 解出即可。解出即可。 y例例1 1.),0(sinyxxyx 求求設(shè)設(shè)解解兩邊同時取自然對數(shù)得兩邊同時取自然對數(shù)得xxylnsinln 求導(dǎo)得兩邊同時對xxxxxyy1sinlncos1 )1sinln(cosxxxxyy)sinln(cossinxxxxxx 解解兩邊同時取自然對數(shù)兩邊同時取自然對數(shù)兩邊同時對求導(dǎo),可得兩邊同時對求導(dǎo),可得x例例2 2 求的導(dǎo)
15、數(shù)求的導(dǎo)數(shù)xxy)(sinyxxysinlnln11lnsincossinyxxxyx (lnsincot )yyxxx (sin ) (lnsincot )xyxxxx,例例3xxy)1 (2y求兩邊同時取自然對數(shù))1ln(ln2xxyxxxxyy21)1ln(122222212)1ln()1 (xxxxyx解解兩邊對兩邊對 x 求導(dǎo)得求導(dǎo)得12)1ln(222xxxyy解解 142) 1(3111)4(1) 1(23xxxexxxyx等式兩邊取自然對數(shù)得等式兩邊取自然對數(shù)得xxxxy )4ln(2)1ln(31)1ln(ln求導(dǎo)得兩邊對x142)1(3111 xxxyy例例4 4.,)4(
16、1) 1(23yexxxyx求設(shè)142) 1( 3111xxxyy例例5 5.11yxxxy求設(shè))1ln()1ln(21lnlnxxxy)1111(2111xxxyy等式兩邊取自然對數(shù)得等式兩邊取自然對數(shù)得解解兩邊同時對兩邊同時對 x 求導(dǎo)求導(dǎo))111(2xxyy)111(112xxxxxy例例6 的導(dǎo)數(shù)的導(dǎo)數(shù)求求)4)(3()2)(1( xxxxy解解兩邊取自然對數(shù)兩邊取自然對數(shù)21lny)2ln() 1ln(xx)4ln()3ln(xx兩邊對兩邊對 x 求導(dǎo)求導(dǎo)21yy11x21x31x41x)4)(3()2)(1(21xxxxy41312111xxxx解解兩邊取自然對數(shù)兩邊取自然對數(shù)兩邊
17、同時對求導(dǎo),可得兩邊同時對求導(dǎo),可得x即即1ln( )3lnln(2)ln(2)2ln(2)3f xxxxx131112( )( )23 22fxf xxxxx3211( )( )322fxf xxxx33223211( )23 22(2)xxfxxxxxx3331211 3131(1)3139339927f例例8dxdyaxaxaxynanaa求求設(shè)設(shè))()()(2121 解解兩邊同時取自然對數(shù)得兩邊同時取自然對數(shù)得)ln()ln()ln(ln2211nnaxaaxaaxay 兩邊對兩邊對 x 求導(dǎo)得求導(dǎo)得nnaxaaxaaxayy 221112211nnaxaaxaaxayy 內(nèi)容小結(jié)內(nèi)容
18、小結(jié)1. 1. 隱函數(shù)求導(dǎo)法則隱函數(shù)求導(dǎo)法則直接對方程兩邊求導(dǎo)。直接對方程兩邊求導(dǎo)。2. 2. 對數(shù)求導(dǎo)法對數(shù)求導(dǎo)法 : :(1)適用于冪指函數(shù)及某些用連乘,連除表示的函數(shù);(2)對方程兩邊取對數(shù),按隱函數(shù)的求導(dǎo)法則求導(dǎo)。定義:定義:所確定的函數(shù).稱此函數(shù)為由參數(shù)方程,關(guān)系間的函數(shù)與確定若參數(shù)方程 xytytx)()(七、七、參數(shù)方程的求導(dǎo)法則參數(shù)方程的求導(dǎo)法則ddddddyytxxt)()(tt例例1 1 解解.arctan)1ln(2dxdyttytx求已知方程dtdxdtdydxdy )1ln()arctan(2ttt2212111tttt21例例2 2解解dtdxdtdydxdyttcos1sin taatattatattatacossin)sin()cos1 ( )sin( )cos1 (2co
溫馨提示
- 1. 本站所有資源如無特殊說明,都需要本地電腦安裝OFFICE2007和PDF閱讀器。圖紙軟件為CAD,CAXA,PROE,UG,SolidWorks等.壓縮文件請下載最新的WinRAR軟件解壓。
- 2. 本站的文檔不包含任何第三方提供的附件圖紙等,如果需要附件,請聯(lián)系上傳者。文件的所有權(quán)益歸上傳用戶所有。
- 3. 本站RAR壓縮包中若帶圖紙,網(wǎng)頁內(nèi)容里面會有圖紙預(yù)覽,若沒有圖紙預(yù)覽就沒有圖紙。
- 4. 未經(jīng)權(quán)益所有人同意不得將文件中的內(nèi)容挪作商業(yè)或盈利用途。
- 5. 人人文庫網(wǎng)僅提供信息存儲空間,僅對用戶上傳內(nèi)容的表現(xiàn)方式做保護(hù)處理,對用戶上傳分享的文檔內(nèi)容本身不做任何修改或編輯,并不能對任何下載內(nèi)容負(fù)責(zé)。
- 6. 下載文件中如有侵權(quán)或不適當(dāng)內(nèi)容,請與我們聯(lián)系,我們立即糾正。
- 7. 本站不保證下載資源的準(zhǔn)確性、安全性和完整性, 同時也不承擔(dān)用戶因使用這些下載資源對自己和他人造成任何形式的傷害或損失。
最新文檔
- 2025年物業(yè)管理師考試試卷及答案解析
- 2025年項(xiàng)目管理師考試題及答案
- 2025年家庭教育與咨詢考試題及答案
- 2025年市場營銷策略考試試卷及答案
- 抖音火花腦機(jī)接口內(nèi)容共享與收益分配協(xié)議
- 農(nóng)業(yè)蟲害防治燈光租賃及蟲情分析服務(wù)協(xié)議
- 抖音火花MCN機(jī)構(gòu)與廣告商內(nèi)容推廣分成協(xié)議
- 電力設(shè)施運(yùn)維維護(hù)補(bǔ)充協(xié)議
- 家庭智能語音控制系統(tǒng)租賃與智能升級合同
- 電商平臺促銷活動期間售后服務(wù)與風(fēng)控服務(wù)合同
- 兒童哮喘降階梯治療
- 《成人心肺復(fù)蘇術(shù)》課件
- 車間照明施工合同范例
- 硫酸安全使用管理及使用制度(4篇)
- 高教版2023年中職教科書《語文》(基礎(chǔ)模塊)下冊教案全冊
- 康復(fù)醫(yī)療行業(yè):社會辦康復(fù)醫(yī)療50企業(yè)報告
- 雪茄知識及侍茄培訓(xùn)
- 三檢制培訓(xùn)資料
- 【高考復(fù)習(xí)】文言文閱讀專題:特殊句式-(公開課課件)
- 超齡員工用工免責(zé)協(xié)議書
- 【基于單片機(jī)的定時智能藥箱設(shè)計(論文)7700字】

評論
0/150
提交評論