1、高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 1一、基本題型用圖表示；求多元函數(shù)的定義域并. 1明不存在的方法。求多元函數(shù)的極限及證. 2. 3 偏導(dǎo)數(shù)及求法. 4 全微分及求法。在、全微分存在的關(guān)系多元函數(shù)連續(xù)、偏導(dǎo)存. 5).(. 6抽象函數(shù)求高階導(dǎo)復(fù)合函數(shù)求導(dǎo)法則).3(. 7種情況隱函數(shù)求導(dǎo)法則總復(fù)習(xí)總復(fù)習(xí) 多元函數(shù)微分學(xué)多元函數(shù)微分學(xué)高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 2. 8方向?qū)?shù)及計(jì)算公式)

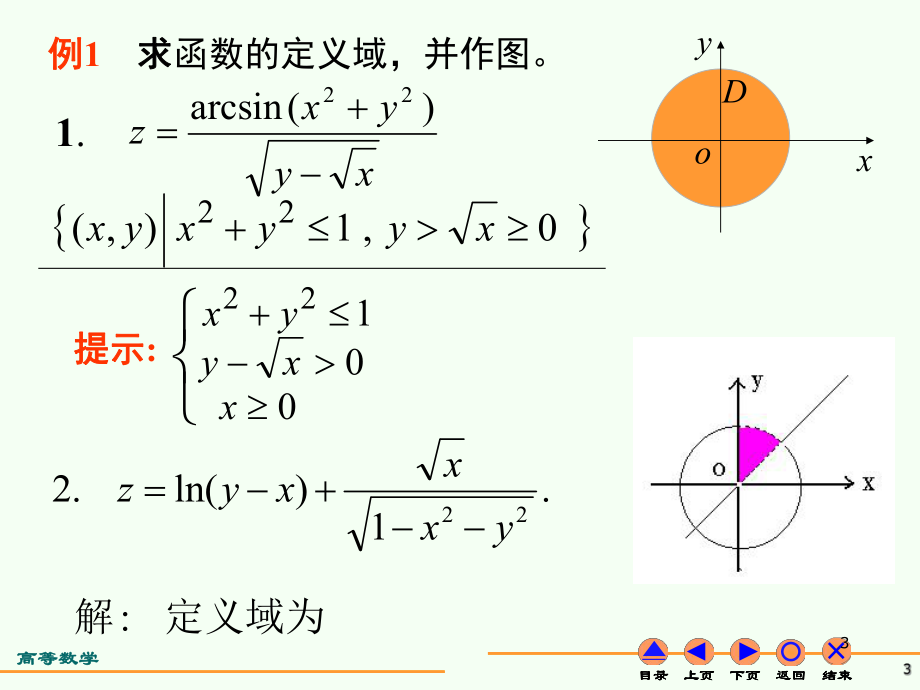
2、.3(. 9種形式面方程空間曲線的切線和法平).2(.10種形式線方程空間曲面的切平面及法.11方法多元函數(shù)的極值及判別乘數(shù)法。多元條件極值的Lagrange.12.13求法區(qū)域上多元函數(shù)最值的高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 30,1),(22xyyxyx1. xyyxz)(arcsin22提示提示:122 yx0 xy0 xDxyo例例1 求求函數(shù)的定義域，并作圖。.1)ln(. 222yxxxyz定義域?yàn)榻?高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄

3、 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 4例例2 設(shè)yxFyyxu23,2且21 ,xxu求yxu,解解21 ,xxu223xxF令23123txxt 2291ttF2222391,yxyyxu高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 51. 22200sinlimyxyxyx提示提示: 222sin0yxyx0ysiny例例3 填空題填空題 11lim. 200yxyxyx)(21lim00yxyxyx22高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目

4、錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 63.225300limyxyxyx提示提示: 22530yxyx3yx 03222222yyxyxyxx4. 設(shè)2),(yyxyxyxf, 則),(yxfx,yxvyxu則),(vuf, )(212vuu 即)(21),(2yxxyxfyx21提示提示: 令高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 75. 設(shè)),(yxf,sin2yxyx0yx,00yx則)1 ,0(xf提示提示:)1 ,0(xfxfxfx) 1 , 0() 1 ,(lim0

5、220sinlimxxx16. f ( x , y ) 在點(diǎn)),(00yx處偏導(dǎo)數(shù), ),(00yxfx存在是 f ( x , y ) 在該點(diǎn)連續(xù) ( ) .(A) 充分條件但非必要 (B) 必要條件但非充分 ;(C) 充要條件 ; (D) 既非充分也非必要條件.D1選擇題 ( 6 - 8 ),(00yxfy高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 87. 設(shè) f ( x , y ) 在點(diǎn)( a , b ) 偏導(dǎo)數(shù)存在 , 則)(),(),(lim0 xbxafbxafx),()(; ),2()(;

6、),(2)(;0)(bafDbafCbafBAxxxB提示提示: 因?yàn)橹灰獙?xiě)結(jié)果 , 可直接用羅必塔法則找答案 ),(),(lim110bxafbxafx原式),(21baf 高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 98. )()1 (lnlim00yxyxxyx1)( ;)( ;0)(DeCB提示提示: 利用令,mxyx即xxym則 原式=yxyxyx200limmmyxxxx2300lim,1當(dāng) m = 3 時(shí),當(dāng) m = 4 時(shí)A(A) 不存在 ;,)1 (lnyxyx高等數(shù)學(xué)高等數(shù)學(xué)目錄 上

7、頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 10例例4 4 證明、判斷下列極限存在與否26300limyxyxyx（2）26300sinlimyxyxyx（3）提示：（1）42200limyxxyyxxky 取時(shí)，有2422200limxkxxkyx42001limkkyx3xky 取時(shí)，有626600limxkxkxyx2001limkkyx3xky 取時(shí)，有6263300sinlimxkxxkxyx2001limkkyx表明上式中極限均不存在。高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄

8、 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 11224400)sin(lim. 4yxyxyx224400limyxyxyx22400limyxxyx22400limyxyyx000.)(lim2222200不存在證明yxyxyxyx:證明1,yx當(dāng)沿路徑時(shí)極限為, 02路徑時(shí)極限為當(dāng)沿xy .所以極限不存在例例5高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 12證明證明：函數(shù) 點(diǎn) 連續(xù)、|),(xyyxf),( 00)0 , 0(0|lim),(lim:0000fxyyxfyxyx證明所以在

9、點(diǎn) 連續(xù) ),( 0000lim)0 , 0()0 ,(lim)0 , 0(00 xxfxffxxx00lim)0 , 0(), 0(lim)0 , 0(00yyfyffyyy所以在點(diǎn) 偏導(dǎo)數(shù)都存在 ),( 00|)0 , 0()0 , 0(yxyfxffyx偏導(dǎo)數(shù)存在、但不可微.例例6高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 130lim2200|limyxyxyx220|limyxyxxyx0212lim220 xxx所以在點(diǎn) 不可微。 ),(00高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄

10、 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 14體會(huì)二元函數(shù)的一些基本概念之間的關(guān)系體會(huì)二元函數(shù)的一些基本概念之間的關(guān)系1、函數(shù)可微，偏導(dǎo)數(shù)不一定連續(xù)；2、當(dāng)yxfxyx,lim00和yxfyyx,lim00不存在時(shí)，也不能斷定0 , 0 xf和0 , 0yf不存在。這只能說(shuō)明偏導(dǎo)數(shù)在點(diǎn)（0，0）處不連續(xù)。yxfz,在點(diǎn)00, yxP處四個(gè)基本概念之間的關(guān)系連續(xù)性偏導(dǎo)數(shù)方向?qū)?shù)可微性可微性條件增強(qiáng)由它可以推出其它三個(gè)概念，反之不一定存在。高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè)

11、 下頁(yè) 返回 結(jié)束 15例例7 求下列函數(shù)的偏導(dǎo)數(shù)和全微分。（1）設(shè))2sin(),(yxeyxfx解解求,)4, 0(xf,)4, 0(yf,)4, 0(fd可先代入部分值，再求導(dǎo)數(shù)。xexfxcos4,1cossin04, 0 xxxxexfyyf2sin, 002cos244, 0yyyfxdfd4, 0高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 16),(zyxuddzzudyyudxxu)1ln(2xxx) 1 , 1 ,(xu5111111 , 1 , 221 , 1 , 2xxu242ln

12、2) 1 , 2(2yyuy55212ln41 , 1 , 2yu52ln2), 1 , 2(zzu2ln21 , 1 , 2zu),(zyxud, )ln(222yxxxuzy求, ) 1 , 1 ,2(ud（2）設(shè)解解高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 17設(shè),arctanyxz 求.yzxz解法一解法一: xzyx11yx211yxyyzyx11yx21xxylnyzxz)1 (2yyxxxxyln例例8解法二解法二: zdyx11yx21yxdyx11yx21)ln(1ydxxxdyxy

13、y高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 18例例9. 設(shè),)(xyfxu 其中,2Cf 求2222yuxu解解:)(xyfxu)(xyfxy; )(xyfyu)(222xyfxyxu)(2xyfxy)(32xyfxy )(32xyfxy )(122xyfxyu )()1(1222222xyfxyxyuxu 高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 19),(2vufxz xzx22x1ffx2例例9),(

14、2xyxyfxz yxz2設(shè)其中具有二階連續(xù)偏導(dǎo)，求f解：解：,xyu 令fuxy xyv,xyv f2xy2f y1fy22fyx高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 202212fyxfyfxyxz2uf22fx223112213yfxfxyfxfx2121fxfxy11211fxfxyx212221fxfxxz),(2xyxyfxz 高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 21例例10 設(shè)),(y

15、xzz 由方程0),(xzyyzxF確定 ,其中F 可微 , 求.yzyxzx解解:)(21yydzzdyxdF 0)(22 xxdzzdxydF得xdFFxzzd122ydFFyz212xFyF21xFyF21yzyxzx yx21FyFx)(2112FyFyzFxFxzzyx高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 22例例11 求曲線023:2333zyxzyx上在點(diǎn)A(1,1.1)處的切線方程和法平面方程。解：解： 方程組兩邊對(duì) x 求導(dǎo)得02210333222z zyzzyyx將點(diǎn)A(1，1

16、，1）代入 2111111zyzy 431411zy3, 1, 441s切線方程311141zyx法平面方程 013114zyx高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 230),(),(tyxFttxfy是由而設(shè)取微分將0),(),(tyxFtxfy0dtFdyFdxFdtfdxfdytyxtxtytxtxtfFFFffFdxdy解解例例12.,dxdyyx求函數(shù)確定的xtfdxdtfdxdyxtyFdxdtFdxdyF高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄

17、 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 24依題意，兩平面平行63421000zyx.2000zyx例例13解：解： 令求曲面平行于平面的各切平面方程。2132222zyx064zyx),(000zyx設(shè)為曲面上的切點(diǎn)，10 x滿足方程),(000zyx切點(diǎn)為, )2,2, 1 ()2, 2, 1(0)2(6)2(4) 1(zyx切平面方程(1)0)2(6)2(4) 1(zyx切平面方程(2)2132,222zyxzyxFzyxzyxn3 ,2 ,26 ,4 ,2高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè)

18、 下頁(yè) 返回 結(jié)束 25例例14 求曲線0122322zyx繞 y 軸旋轉(zhuǎn)一周生成的曲面在點(diǎn)2, 3, 0上的切平面與xoy平面的夾角。解解 旋轉(zhuǎn)曲面1223:222yzxzyxn3,2,322, 3, 0在點(diǎn)23, 32, 0nxoy平面上1, 0, 01n11cosnnnn153153arccos高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 26,xyexz 證明曲面在任意點(diǎn)),(zyxM解解: 令, zexFxy則曲面在點(diǎn) M 的法向量為zyxFFFn, ,xyxyexye而zyxOM,OMnxye

19、yz0故.OMn 的法線與向量 垂直 .OM,xye1xyxyeyex例例15. 設(shè)曲面的方程為高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 27求最大長(zhǎng)方體xOy解解 設(shè)長(zhǎng)方體的一個(gè)頂點(diǎn) 在錐面，則長(zhǎng)方體),(zyxM)0, 0, 0()2(4zyxzxyV)()2(),(222yxzzxyzyxF作）（令102)2(xzyFx）（ 202)2(yzxFy）（ 302zxyFz）（ 4222yxz例例1622yxz2z在圓錐面與平面所圍成的錐體內(nèi)作底面與面平行的長(zhǎng)方體，的體積。的體積：高等數(shù)學(xué)高等數(shù)學(xué)目

20、錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 28將式乘以x與式乘以y相比較得 yx 將 代入式并由式得 yx xz2232x所以得唯一駐點(diǎn)為 ),(34232232依題意必有最大值，從而長(zhǎng)方體的最大體積為276434232242)()(V22 z高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 29例例17. 求點(diǎn) (1, 2, 0) 到曲面02yxz的最短距離 .解解: 問(wèn)題為222)2() 1(zyxd02yxz( 條件 )設(shè)222

21、)2() 1(zyxF)(2yxz 令0)1(2yxFx0)2(2xyFy022zzFz02yxzF解得)0,0, 1(),(zyx)0,2,0(),(zyx此兩點(diǎn)到曲面的距離為;2)0,0, 1(d1)0,2,0(d故1)0,2,0(d)min(為最短 .高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 30. 1, 3)0(zyezyezeyzyyxxxx的最大值，并證明求滿足和、設(shè)三個(gè)實(shí)數(shù), 3zeyx,3xeyzzyeyxfx),(令)3(yeyexx)23(yeyexfxx)23(yeeyfxx解解

22、023023yeyfyexfxx令1, 0yx唯一駐點(diǎn)例例1818高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 31, 2)1 , 0(22xfA而, 1)1 , 0(2yxfB2)1 , 0(22yfC, 03) 1()2()2(22BAC0,A且1),(yxf. 1zyex從而，即為最大值處取得極值在點(diǎn)1) 1 , 0() 1 , 0(),(fyxf高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 32是直線直線設(shè)函

23、數(shù)lzyxyu,)(cos22解.coscoscoszuyuxulu的方向向量先求 l,5:0420231:1上的投影在平面zyxzyzxl的方向?qū)?shù)及沿直線在點(diǎn)試求函數(shù)lPu) 1 , 0 , 0().(軸正向?yàn)殇J角與規(guī)定zlugradp例例19高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 33作平面束過(guò)直線1l0)42(23zyzx04)221(3zyx垂直的條件由與平面022131 185 的方程直線l020560zyxzyx的方向向量l1561110kjilkji1174軸正向夾角為銳角與zl高等

24、數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 34kjilS11740取的方向余弦l,1864cos,cos1867 .cos18611 , 0)2sin(ppxyyxu, 1)12sin(2ppzxyxyu, 0)2(3ppzyzuppzuyuxulu)coscoscos(1867pkzujyuixugradu) 1 , 0 , 0(0 , 1, 0 高等數(shù)學(xué)高等數(shù)學(xué)目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 目錄 上頁(yè) 下頁(yè) 返回 結(jié)束 35例例20. 在曲面21222zyx上求出一點(diǎn) M , 使),(zyxf222zyx沿著點(diǎn))1 , 1 , 1(A)1 ,0,2(B的方向?qū)?shù)具有最大值 . 解解: ,0, 1, 1 AB其方向余弦為,0